| [820] jonas | 2017-03-09 16:13:27 |
 Yield már olyan alakra hozta, ahol két kétváltozós valós másodfokú egyenletnek kell a közös gyökét keresni. Ilyen egyenletrendszerre van általános egzakt megoldás, négyzetgyökökkel, de ez kevéssé ismert. Ha viszont a gyakorlatban találkozol egy ilyen egyenletrendszerrel, és akár szimbolikus megoldást keresel, akár megbízható numerikusat, nem könnyű meglévő szoftver implementációt találni. A Wolfram Alpha érthető befejezés volt.
|
| Előzmény: [819] Róbert Gida, 2017-03-09 15:07:09 |
|
| [819] Róbert Gida | 2017-03-09 15:07:09 |
 Akkor tulajdonképpen a Wolfram Alpha oldotta meg a problémát: Wolfram
itt a második alternatív alaknál nullára rendezte és felírja u*conj(u) alakban a kifejezést, én csupán ezt az alakot gyöktelenítettem. A Reduce[]-ra egyébként True-t ír, azaz ténylegesen be tudja bizonyítani az egyenlőtlenséget valós \(\displaystyle x,y,z\)-re.
A megoldásodból az is látható, hogy nemnegatív valós \(\displaystyle x,y,z\)-re egyenlőség csak a trivi \(\displaystyle x=y=z\) esetben van.
|
| Előzmény: [818] yield, 2017-03-09 10:43:05 |
|
| [818] yield | 2017-03-09 10:43:05 |
 Feladat sokkal nehezebb része Róbert Gida elvégezte! Bridge játéknál azt mondják, hogy "a lordok licitálnak a szolgák lejatsszák az osztást".
Egyenlőség akkor van ha "u" valós és képzetes része = 0
1. Ha z = 0, akkor csak x = y = 0 lehet.
2. Ha z <> 0, akkor egyenletek homogén alakja miatt behelyettesíthető a = \(\displaystyle \frac{x}{z}\), b = \(\displaystyle \frac{y}{z}\). Két egyenletünk Wolframalphának beadva: link
Négy megoldás van:
(\(\displaystyle \frac{x}{z}\),\(\displaystyle \frac{y}{z}\)) = (a,b) = (1,1), (-7.48085, -5.49553), (-0.181966, 1.36126), (0.734614, -0.133675)
|
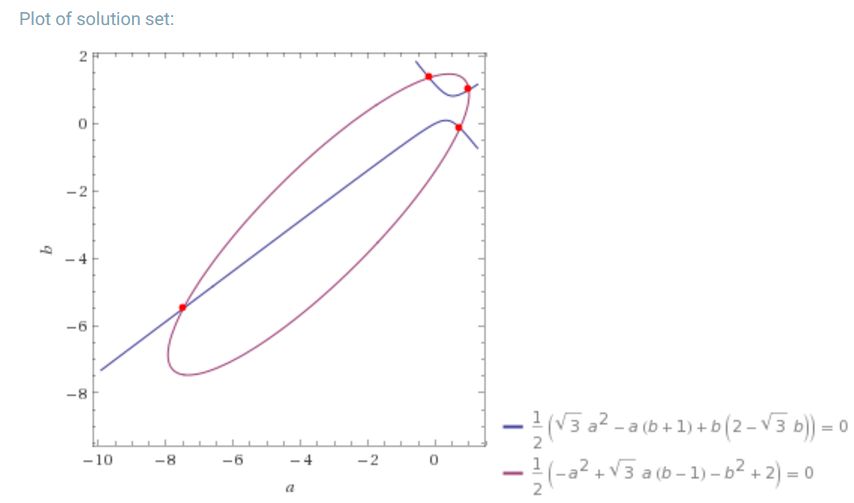 |
| Előzmény: [817] csábos, 2017-03-08 20:43:16 |
|
|
| [816] Róbert Gida | 2017-03-07 23:26:59 |
 Legyen \(\displaystyle f(x,y,z)=x^4+y^4+z^4+(\sqrt 3-1)xyz(x+y+z)-\sqrt 3(x^3y+y^3z+z^3x)\), kell \(\displaystyle f(x,y,z)\ge 0\). Belátom, hogy \(\displaystyle f(x,y,z)\) éppen egy komplex szám abszolútértékének a négyzete, így nemnegatív. Legyen \(\displaystyle S=\sqrt 3\) és \(\displaystyle E=1+\frac {i}{S}\), ekkor \(\displaystyle f(x,y,z)=|u|^2\), ahol: \(\displaystyle u=\frac 12 ESx(ix-z)-\frac 34 yE^2(ix+y)+iyz+z^2\).
|
| Előzmény: [815] csábos, 2017-03-06 23:44:09 |
|
| [815] csábos | 2017-03-06 23:44:09 |
 Kitaláltam egy feladatot. Tud valaki rá jobbfajta megoldást?
Bizonyítsuk be, hogy
\(\displaystyle (x^4+y^4+z^4)+(\sqrt 3 -1 )xyz(x+y+z)\geq
\sqrt 3(x^3y+y^3z+z^3x)
\)
Mikor áll fönt egyenlőség?
|
|
| [814] nadorp | 2017-02-01 23:59:18 |
 Egy kiegészítés.
Bebizonyítjuk, hogy ha \(\displaystyle f^{'}(t)=f(f(t))\) teljesül minden valós t-re, akkor létezik f-nek fixpontja. Ebből már következik, hogy a [813]-ban megadott linken levő Taylor-sor család megadja az összes megoldást.
Tegyük fel, hogy f-nek nincs fixpontja. Ekkor vagy \(\displaystyle f(t)-t>0\) vagy \(\displaystyle f(t)-t<0\) teljesül minden valós számra, hiszen f folytonos is.
1.eset: \(\displaystyle f(t)>t\)
Legyen \(\displaystyle t\geq0\). Ekkor \(\displaystyle f(t)>t\geq0\) miatt \(\displaystyle f(f(t))>f(t)\) is teljesül, azaz
| \(\displaystyle f^{'}(t)>f(t)>0 \) | \(\displaystyle {(1)}\) |
Ebből egyrészt következik hogy \(\displaystyle t\geq0\) esetén \(\displaystyle f(t)\) szigorúan monoton nő, tehát \(\displaystyle t\geq f(0)>0\) esetén f-nek létezik egyértelmű \(\displaystyle f^{-1}(t)\geq0\) inverze. Az eredeti egyenletet ezzel felírva
\(\displaystyle f^{'}(f^{-1}(t))=f(t)\)
| \(\displaystyle ({f^{-1}})^{'}(t)=\frac1{f(t)} \) | \(\displaystyle {(2)}\) |
Másrészt (1) mindkét oldalát megszorozva \(\displaystyle e^{-t}\)-vel és rendezve
\(\displaystyle (f^{'}(t)-f(t))e^{-t}>0\)
\(\displaystyle (f(t){e^{-t})}^{'}>0\)
Tehát az \(\displaystyle f(t)e^{-t}\) függvény \(\displaystyle t\geq0\) esetén szigorúan monoton nő, így
\(\displaystyle f(t)e^{-t}\geq f(0)\)
| \(\displaystyle f(t)\geq f(0)e^t \) | \(\displaystyle {(3)}\) |
Összevetve (2)-t és (3)-at \(\displaystyle t>f(0)>0\) esetén kapjuk, hogy
\(\displaystyle ({f^{-1}})^{'}(t)\leq\frac1{f(0)}e^{-t}\)
\(\displaystyle \int_{f(0)}^t({f^{-1}})^{'}(s)ds\leq\frac1{f(0)}\int_{f(0)}^te^{-s}ds\)
\(\displaystyle f^{-1}(t)\leq\frac1{f(0)}(e^{-f(0)}-e^{-t})<\frac{e^{-f(0}}{f(0)}\)
Ez viszont ellentmondás, mert \(\displaystyle t>f(0)>0\) esetén \(\displaystyle f^{-1}(t)\) nem lehet korlátos.
2.eset: \(\displaystyle f(t)<t\)
Legyen \(\displaystyle t\leq0\). Ekkor \(\displaystyle f(t)<t\leq0\) miatt \(\displaystyle f(f(t))<f(t)\) is teljesül, azaz
\(\displaystyle f^{'}(t)<f(t)<0\)
Ebből következik hogy \(\displaystyle t\leq0\) esetén \(\displaystyle f(t)\) szigorúan monoton csökken.
Legyen most \(\displaystyle a=f(0)<0\). Ekkor a monoton csökkenést felhasználva
\(\displaystyle f(a)>f(0)=a>f(a)\)
Ez pedig ellentmondás.
|
| Előzmény: [813] nadorp, 2017-01-28 09:05:15 |
|
| [813] nadorp | 2017-01-28 09:05:15 |
 Elindultam abból, hogy keressünk olyan megoldást, ahol létezik a, hogy f(a)=a. Eljutottam az f(f(x)) függvény n-dik deriváltjának a képletéig, ami alapján elkezdtem Taylor-sorba fejteni f-et a fixpont körül, felhasználva a Faà di Bruno Formulát. Ez előbb-utóbb elég csúnya lesz, ezért rákerestem a neten (hátha...) és ezt találtam, ami megfelel a fenti gondolatmenetnek ( az utolsó hozzászólás a lényeges):
lásd itt
|
| Előzmény: [812] Sinobi, 2017-01-26 00:58:28 |
|
| [812] Sinobi | 2017-01-26 00:58:28 |
 Milyen \(\displaystyle f\) függvények vannak, amelyeknek a deriváltjuk megegyezik az ismételtjükkel, azaz: \(\displaystyle f'(t)=f(f(t))\)?
Ezt, vagy az ilyesmiket hogyan kell/lehet?
|
|
|
| [810] yield | 2017-01-07 19:40:51 |
 Ha felírjuk a koszinusztételt erre a háromszögre, akkor kapunk egy egyenletet q-ra. Ennek csak q =1 esetén lesz megoldása az alábbi állítás alapján: "Tegyük fel, hogy a (m/n) már nem egyszerűsíthető tört gyöke az f egész együtthatós polinomnak. Ekkor a számláló osztja f konstans tagját, a nevező pedig a főegyütthatóját"
|
| Előzmény: [809] marcius8, 2017-01-04 12:56:03 |
|
| [809] marcius8 | 2017-01-04 12:56:03 |
 Pontosítom az előző kérdést. Ha a háromszög szabályos, és oldalainak hossza 1, akkor az ilyen háromszög. De van-e nem szabályos háromszög, amely megfelel a feltételeknek, azaz egyik szöge 60°, oldalai racionális hosszúak és egy mértani sorozat nem feltétlenül egymást követő tagjai.
|
| Előzmény: [808] marcius8, 2017-01-04 09:44:39 |
|
| [808] marcius8 | 2017-01-04 09:44:39 |
 Van-e olyan derékszögű háromszög, amelynek oldalai racionális hosszúak, és oldalai egy mértani sorozat nem feltétlenül egymást követő elemei?
Van-e olyan háromszög, amelynek egyik szöge 60° vagy 120°, amelynek oldalai racionális hosszúak, és oldalai egy mértani sorozat nem feltétlenül egymást követő elemei?
|
|
| [807] Sinobi | 2016-12-24 14:59:20 |
 Na jó, a görbület integrálja rész hülyeség.
Olyan kéne, hogy a csúcsokban úgy viselkedjen hogy az R sugarú kör hossza tartson valami 2pi*R*C, C fix számhoz. Tetraéderre C=1/2 — kihajtogatás után látszik, hogy egy kör egy félkörbõl áll.
|
|
| [806] Sinobi | 2016-12-24 14:36:20 |
 Tudtok (vagy tudtok keresni) olyan, 3d beágyazott felületet, amelynek majdnem mindenhol konstans a görbülete, maximum véges sok pontban nem?
Például a tetraéder felszíne olyan, hogy majdnem mindenhol 0 a görbület, csak 4 helyen van elrontva, de, ahol el van rontva, ott a csúcsban bármekkora kis környezetben 1/4 a görbület integrálja.
Ilyesmi kéne nekem, csak, 0 helyett állandó pozitív vagy negatív görbülettel, és, hogy a kihagyott pontokban is, az elõbbi értelemben vett "szép" legyen, hogy a pont kis környezetein a görbület integrálja tartson valami konkrét számhoz.
Nem baj, ha van határa, vagy csak 1 csúcsot vizsgál hogy hogyan néz ki, de zárt felületnek jobban örülnék.
(nem ismerem a szavakat magyarul vagy angolul)
|
|
| [805] Kemény Legény | 2016-06-28 15:21:16 |
 Sajnos nem néztem utána a C++ implementációnak, úgy tűnik, nincs ilyen. Én csak azt láttam, amikor google-ben rákerestem, hogy mást is érdekelt a dolog, nekem pedig Matlabban volt a legegyszerűbb megoldani az egészet, innen gondoltam, más nyelven is sikerült volna.
|
| Előzmény: [804] jonas, 2016-06-28 14:01:44 |
|
| [804] jonas | 2016-06-28 14:01:44 |
 Remek! Korábban kerestem már implementációt, ami bármilyen ferde többváltozós normális eloszlás kumulatív eloszlásfüggvényét kiszámolja. (Black box szinten kellett volna, nem megérteni.) Akkor nem találtam ilyet.
Most a te útmutatásod alapján tényleg találtam ilyet: octaveforge statistics-1.2.4 csomagban van mvncdf nevű függvény, ami ezt csinálja. (Nem is új, évekkel korábbi verzióban is ott volt már.) Ez ugyan teljesen elegendő lesz nekem, ha valamikor újra ilyet szeretnék kiszámolni, de ha már felvetetted, kíváncsi vagyok. Melyik C++ nyelvű implementációra gondoltál? Azt tudom, hogy a GSL könyvtárban nincs ilyen, a boost random csomagban nincs, és máshol sem láttam.
|
| Előzmény: [802] Kemény Legény, 2016-06-28 00:36:51 |
|
|
| [802] Kemény Legény | 2016-06-28 00:36:51 |
 Az általam megadott képlettel szerencsére sokkal gyorsabban lehet választ kapni, mint Monte-Carlo-jellegű szimulációval, ugyanis rengeteteg programnyelven (R, C++, Matlab) elérhető olyan függvény, ami a megadott mátrixszal és vektorral számol eloszlásfüggvényt többváltozós normális eloszlásra. Például Matlabbal a következő tesztpéldákat számoltam végig:
&tex;\displaystyle \mu = [8.7; 9.4; 9.6; 9.7; 9.2; 9.1]&xet;, &tex;\displaystyle \sigma = 2.0&xet;
Ekkor &tex;\displaystyle p = 0.248542598153021&xet; az 'mvncdf' függvény (multivariate normal cumulative distribution function) által adott érték, míg a lassabb 10milliós elemszámú (Monte-Carlo) szimuláció eredménye: &tex;\displaystyle 2486815/10000000&xet;.
Vagy &tex;\displaystyle \sigma = 0.5&xet; és ugyanezen &tex;\displaystyle \mu&xet; mellett: &tex;\displaystyle p = 0.53444797435079&xet;, a szimuláció &tex;\displaystyle 5343301/1000000&xet;-t adott.
Vagy &tex;\displaystyle \sigma = 0.1&xet; és ugyanezen &tex;\displaystyle \mu&xet; mellett: &tex;\displaystyle p = 0.997490348287471&xet;, a szimuláció &tex;\displaystyle 9974678/10000000&xet;-t adott eredményül.
Vagy &tex;\displaystyle \sigma = 30&xet; esetén, &tex;\displaystyle p = 0.171608841494814&xet; esetén a szimuláció &tex;\displaystyle 1716277/10000000&xet;-t adott eredményül.
Mindezek abszolút összhangban vannak: ha &tex;\displaystyle \sigma\to \infty&xet;, akkor &tex;\displaystyle p\to \frac{1}{6}&xet;; vagy ha &tex;\displaystyle \sigma\to 0&xet;, akkor &tex;\displaystyle p\to 1&xet; vagy &tex;\displaystyle p\to 0&xet; attól függően, hogy &tex;\displaystyle \mu_1&xet; a legkisebb vagy sem.
Még egyszer a lényeg: a többváltozós eloszlásfüggvényből számolt eredmény kb. &tex;\displaystyle 0.1&xet; másodperc alatt lefutott, a szimuláció ennél jóval lassabb, főleg ha több kísérletet akarunk átlagolni...Azaz, ha &tex;\displaystyle [\mu,\sigma]&xet; értékei ismertek, én bőven &tex;\displaystyle 1&xet; másodpercen belül tudom szolgáltatni a pontos eredményt.
|
| Előzmény: [801] Zoltano86, 2016-06-28 00:03:17 |
|
| [801] Zoltano86 | 2016-06-28 00:03:17 |
 A 6 normális eloszlás 6 kutya várható ideje egy adott futamon. A valség pedig a nyerés valsége egy adott kutyára. Angol futamokat nézek, ahol statisztika van visszamenôleg elôzô futamokra. Ebbôl jönnek a várható átlagok. Futam elôtt nagyon mozognak az oddsok sokszor lefelezôdnek akár. Mondanom sem kell mennyi pénz van benne ha elcsípsz egy ilyet. Eddig excellel próbálkoztam véletlen számokat generálva. Viszonylag rövid idô alatt kapok valségeket, de persze ez pontatlan, és nem a legszebb módja a számolgatásnak.
|
| Előzmény: [800] Kemény Legény, 2016-06-27 13:31:30 |
|
| [800] Kemény Legény | 2016-06-27 13:31:30 |
 Sajnos az utolsó lépés nem működik, nem ekvivalens az eredeti feladattal a &tex;\displaystyle Z&xet; eloszlásfüggvényének elemzése, így marad az, hogy adott várható értékű és kovarianciamátrixú többdimenziós normális eloszlás eloszlásfüggvényének az origó-beli értékeként adjuk meg a megoldást.
|
| Előzmény: [799] Kemény Legény, 2016-06-27 12:49:03 |
|
| [799] Kemény Legény | 2016-06-27 12:49:03 |
 Megkérdezhetem, hogy honnan származik a feladat; tudjuk esetleg biztosan, hogy kell lennie zárt alaknak?
Mindenesetre a következő tervet látom a számolásra, de még nem volt erőm teljesen mindent végigszenvedni rajta.
1. lépés: Ha &tex;\displaystyle 6&xet; helyett csak &tex;\displaystyle 2&xet; változónk van, akkor &tex;\displaystyle X_1-X_2&xet; eloszlása &tex;\displaystyle N(\mu_1-\mu_2, 2\sigma^2)&xet;, a megoldás &tex;\displaystyle \Phi\left(\frac{\mu_2-\mu_1}{\sqrt{2}\sigma}\right)&xet;. Innen jöhet a következő gondolat.
2. lépés: Vezessük be az &tex;\displaystyle Y = (X_1-X_2,\cdots, X_1-X_6)&xet; valószínűségi vektorváltozót, ennek az eloszlásfüggvényét kellene kiszámolni a &tex;\displaystyle [0,0,0,0,0]&xet; pontban. Mivel független normálisok lineáris transzformáltja, &tex;\displaystyle Y&xet; egy többváltozós normális &tex;\displaystyle \mu = (\mu_1-\mu_2,\cdots,\mu_1-\mu_6)&xet; várható értékkel, és egy &tex;\displaystyle 5\times5&xet;-ös &tex;\displaystyle S&xet; kovarianciamátrixszal, aminek főátlója &tex;\displaystyle 2\sigma^2&xet;, minden más eleme &tex;\displaystyle \sigma^2&xet;.
3. lépés: Egyszerű ujjgyakorlat, hogy &tex;\displaystyle det(S)=6\sigma^{10}&xet;.
4. lépés: Szintén ujjgyakorlat, hogy &tex;\displaystyle 6\sigma^2\cdot S^{-1}&xet; olyan mátrix, aminek főátlója csupa &tex;\displaystyle 5&xet;-ös, mellékátlója csupa &tex;\displaystyle -1&xet;.
5. lépés: Szintén kiszámolhatóak &tex;\displaystyle S&xet; (és onnan &tex;\displaystyle S^{-1}&xet;) sajátértékei: &tex;\displaystyle 6\sigma^2,\sigma^2,\sigma^2,\sigma^2,\sigma^2&xet;.
6. lépés: Kiszámoljuk a sajátvektorokat is. Sajnos az &tex;\displaystyle [1,1,1,1,1]&xet; és &tex;\displaystyle [1,-1,0,0,0]&xet;,&tex;\displaystyle \cdots&xet;,&tex;\displaystyle [1,0,0,0,-1]&xet; választás nem a legjobb, a fenti helyett egy ortonormált rendszert kellene keresni (az &tex;\displaystyle 1&xet; sajátértékhez tartozó sajátaltérből egymásra és &tex;\displaystyle [1,1,1,1,1]&xet;-re is merőleges egységvektorokat kellene keresnünk). Gram-Schmidt-ortogonalizációs lépésekkel például ezt meg lehetne tenni...
7. Ha már van ortonormált sajátbázisunk, akkor ezek alapján bevezetünk egy új &tex;\displaystyle Z&xet; változót az &tex;\displaystyle Y&xet;-ok megfelelő lineáris transzformáltjaként úgy, hogy a &tex;\displaystyle Z&xet; kovariancamátrixa diagonális legyen.
8. lépés: Az &tex;\displaystyle Y&xet; eloszlásfüggvénye a &tex;\displaystyle [0,0,0,0,0]&xet; pontban adta a választ az eredeti kérdésre, most a transzformált &tex;\displaystyle Z&xet; eloszlásfüggvényét kellene meghatározni egy pontban, de ennek már diagonális a kovarianciamátrixa, az integrál könnyen lebontható egyszerűbb (egyváltozós) integrálok szorzatára, és akkor a &tex;\displaystyle \Phi&xet;-vel kifejezhető egy zárt alak.
|
| Előzmény: [798] Zoltano86, 2016-06-25 18:39:17 |
|
| [798] Zoltano86 | 2016-06-25 18:39:17 |
 Koszonom szepen, bar en is kivancsi vagyok hogy van-e szebb alak
|
|
| [797] Kemény Legény | 2016-06-25 18:17:07 |
 Ez a "nem szép integrálás" lenne az igazi feladat. Vagy technikailag azt mondod, hogy ez is végeredmény? Engem azért érdekelne egy zárt alak a végeredményre...
&tex;\displaystyle \int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(y-\mu_1)^2}{2\sigma^2}}\left(1-\Phi\left(\frac{y-\mu_2}{\sigma}\right)\right)\cdot\cdots\cdot\left(1-\Phi\left(\frac{y-\mu_6}{\sigma}\right)\right)dy &xet;
|
| Előzmény: [795] S.Ákos, 2016-06-25 16:40:19 |
|
| [796] Zoltano86 | 2016-06-25 17:03:01 |
 Kemeny Legeny mar erti a feladatot. Elnezest a hanyag megfogalmazasert, de azt kellene kiszamolni mekkora a valsege hogy pont x1 lesz a legkisebb valsegi valtozo.
|
|







