| [89] Sirpi | 2004-02-27 13:29:15 |
 Szia Nadorp!
Köszi a megoldást, teljesen jó. Amúgy ez az alapötlete az én konstrukciómnak is, amit mondjuk hétfőn beírok, ha addig nem csap le rá senki (hétvégén síelek :-) ).
S
|
| Előzmény: [88] nadorp, 2004-02-27 10:47:48 |
|
| [88] nadorp | 2004-02-27 10:47:48 |
 Felső korlát megadása Sirpi [75] feladatára.
Legyenek m,n pozitív egészek és legyen (m,n)=d. Ekkor legfeljeb m+n-d-1 darab valós szám adható meg úgy, hogy közülük bármely szomszédos n darab összege pozitív és bármely szomszédos m darab összege negatív.
Tegyük fel, hogy az állítással ellentétben létezik m+n-d darab, a feltételeknek megfelelő szám. Legyenek ezek x1,x2,...xn+m-d.Előrebocsátunk két nyilvánvaló észrevételt:
1, Ha létezik a feltételeknek megfelelő sorozat, akkor olyan is létezik,amelyben bármely n darab szomszédos összege negatív és bármely m darab szomszédos összege pozitív ui. csak minden elemet meg kell szorozni -1-gyel.
2, n nem osztója m-nek és viszont
Az 1. észrevétel miatt feltehető, hogy n<m.Osszuk el m-et maradékosan n-nel:
m=nx1+r1 0<r1<n, d|r1
Mivel az első m szám összege negatív, de bármely n szomszédos összege pozitív, ezért
x1+x2+...xr1<0. Teljesen hasonlóan
x2+x2+...xr1+1<0
...
xn-d+1+...xn+r1-d<0
Azt kaptuk, hogy létezik n+r1-d darab szám, hogy közülük bármely r1 szomszédos összege negatív és bármely szomszédos n összege pozitív, de ekkor az 1.észrevétel miatt létezik n+r1-d darab szám, hogy közülük bármely r1 szomszédos összege pozitív és bármely szomszédos n összege negatív.
A fenti gondolatmenetet most a r1,n számokra alkalmazva,ha
n=r1x2+r2 0<r2<r1, d|r2
akkor létezik r1+r2-d darab szám, hogy közülük bármely r2 szomszédos összege pozitív és bármely szomszédos r1 összege negatív.
A fenti folyamat vég nélkül nem folytatható, ezért lesz egy olyan k index, hogy
rk-1=rkxk+1+rk+1 0<rk+1<rk, d|rk+1
rk=rk+1xk+2+d
és létezik rk+1+d-d=rk+1 darab szám, hogy bármely szomszédos d összege pozitív és az rk+1 összege negatív. Ez viszont a 2. észrevétel miatt ellentmondás.
|
|
|
| [86] Sirpi | 2004-02-26 14:48:53 |
 Ha bonyi a bizonyításod egy része, akkor írd le csak a felső becslése(i)d bizonyítását. Amit én adtam megoldást a felső korlát élességére, az konstruktív, és aránylag egyszerű, ha nem lesz más megoldó, akkor azt a részt beírom én. Jó lesz így?
Sirpi
|
| Előzmény: [85] nadorp, 2004-02-26 14:43:47 |
|
| [85] nadorp | 2004-02-26 14:43:47 |
 Szia Sirpi !
Kösz a segítséget, így már könnyebb volt (0...0). Én is próbálkoztam a relatív prím megoldásba "beszúrkálni", csak az volt a baj, hogy két elem közé d darab elemet és a maradék d-1 elemet meg valahogy elosztogatni.
A megoldást nem tudom, érdemes-e közölni, mert szerintem egy picit hosszú a fórumhoz. A másik baj az vele, hogy relatív prímekre felhasználtam egy kis lineáris algebrát (rezultáns) és csak egzisztenciát bizonyít, tehát nem konstruktív.
N.P.
|
| Előzmény: [84] Sirpi, 2004-02-26 10:31:48 |
|
| [84] Sirpi | 2004-02-26 10:31:48 |
 Szia nadorp!
Gratulálok, lényegében megoldottad a feladatot! Az n+m-d-1 valóban éles korlát minden n,m-re (a d=1 esetre is jó). Az, hogy a korlát elérhető nem relatív prím esetben, nem olyan nehéz. Legyen (n,m)=d, n=dn', m=dm', és tegyük fel, hogy a relatív prím n',m'-re már van n'+m'-2 hosszú jó sorozatunk.
Ezt kellene "felduzzasztani", pl. bármely két elem közé, sőt, legelőre és leghátulra is d-1 új elemet (de vajon mit?) betenni, ekkor ugyanis n'+m'-2+(n'+m'-1)(d-1)=n'd+m'd+d-1=n+m-d-1 elemű lesz a felduzzasztott sorozat. Remélem, így már összeáll a teljes bizonyítás.
Sirpi
|
| Előzmény: [83] nadorp, 2004-02-26 09:09:55 |
|
| [83] nadorp | 2004-02-26 09:09:55 |
 Szia Sirpi !
Az általad kitűzött példához részeredményein vannak, de egyelőre nem tudom eldönteni, hogy jó helyen kereskedek-e. Jelölje S a maximális elemszámot. Ekkor
1, Ha n=1,m=1, akkor nincs megoldás
2, Ha n|m, akkor S=m-1 ( ugyanez igaz fordítva)
3, Bizonyítottam, hogy S n+m-2 n+m-2
4, Bizonyítottam, hogy m és n relatív prímek, akkor S=n+m-2 ( ez a bizonyítás sajnos nem teljesen elemi )
5, Bizonyítottam, hogy ha (m,n)=d és d 2, akkor S<=m+n-d-1 2, akkor S<=m+n-d-1
6, Egyelőre még nem látom, hogy az 5-ben levő felső korlát elérhető-e.
Üdv
N.P.
|
| Előzmény: [75] Sirpi, 2004-02-17 08:51:41 |
|
|
|
| [80] lorantfy | 2004-02-19 21:14:48 |
 Kedves Géza és Erdős-Graham Érdeklődők!
Ma voltam bent a Rényi Intézetben és már meg is van a cikk, most scanneltem és már tudom is küldeni minden érdeklődőnek. 5 oldal (persze angolul) 1 Mega. Nagyon érdekes én most "rágcsálom".
|
| Előzmény: [79] Kós Géza, 2004-02-19 20:50:28 |
|
| [79] Kós Géza | 2004-02-19 20:50:28 |
 Kicsit keresgéltem a citeseeren, és a következőt találtam:
P. Erdős and R. L. Graham. On packing squares with equal squares. J. Comb. Theory (A), 19, 1975, 119-123.
Keresd a "Journal of Combinatorial Theory, Series A" című lapot a Rényi Intézetben.
|
| Előzmény: [78] Kós Géza, 2004-02-19 20:33:42 |
|
|
| [77] Gubbubu | 2004-02-19 20:26:14 |
 Kedves László, kedves Onogur!
Jókívánságaitokat köszönöm, új erőre kaptam tőlük. Holnap talán eljutok az ELTE matematika könyvtárába (egyszer már próbáltam, kevés sikerrel, de ígérték, hogy utánanéznek bizonyos dolgoknak ez ügyben). Egyszóval annak ellenére, hogy egy matematikusnak talán tényleg több esélye van, én is folytatom a keresést a magam igen szerény eszközeivel.
Üdv:G.
|
| Előzmény: [69] lorantfy, 2004-02-12 07:46:02 |
|
| [76] Kiss Demeter | 2004-02-17 21:44:37 |
 Sziasztok!
Megtetszett a másodfokú polinomos példa és írtam egy programot, mely lorantfy jelölését használva a c,d,e,f,g és b számokat keresi meg. (Azaz a másodfokú polinom x=0,1,2,3,4 helyeken felvett értekeinek pozitív négyzetgyökeit).
Sajnos még nem talált a feladat állításának megfelelő számötöst, de találtam néhány számnégyest:(az i. oszlopban lévő szám az i-1 helyen felvett érték pozitív négyzetgyöke, továbbá az utolsó szám a b értéke):
6, 23, 32, 39, 246
39, 70, 91, 108, 1689
108, 157, 194, 225, 6492
225, 296, 353, 402, 18495
16, 87, 122, 149, 3656
402, 499, 580, 651, 43698
51, 148, 203, 246, 9651
651, 778, 887, 984, 90741
147, 302, 401, 480, 34797
984, 1145, 1286, 1413, 171384
79, 242, 333, 404, 26161
59, 228, 317, 386, 24251
1413, 1612, 1789, 1950, 300987
324, 557, 718, 849, 102636
1950, 2191, 2408, 2607, 498990
2607, 2894, 3155, 3396, 789393
|
|
| [75] Sirpi | 2004-02-17 08:51:41 |
 Sziasztok!
Ha minden igaz, ezen a fórumon még nem szerepelt ez a feladat, úgyhogy kitüzöm:
Adott n és m pozitív egészekre legfeljebb hány egész számot lehet megadni úgy, hogy bármely egymás után következö n összege szigorúan pozitív, míg bármely egymás utáni m összege szigorúan negatív legyen?
|
|
| [74] Csizmadia Gábor | 2004-02-16 22:34:40 |
 A feladat egyszerű addíciós tétellel kijön, de azért szerintem ez is szép: Legyen z=a+bi komplex szám. Jelölje z arkuszát
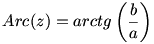
abszolút értékét
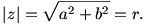
Könnyen bizonyítható az alábbi egyszerű tétel:
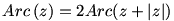
Vegyünk fel egy derékszögű koordinátarendszert, és a z, illetve z+|z| számoknak megfelelő (a;b) és (a+r;b) pontokat. Ekkor (0;0), (a;b), (a+r;b), (r;0) pontok egy rombuszt alkotnak, aminek a (0;0)-n és (a+r;b)-n átmenő egyenes átlója, tehát ennek az egyenesnek az x-tengellyel bezárt szöge valóban fele a (0;0)-n és (a;b)-n átmenő egyenes x-tengellyel bezárt szögével. (qed) Mármost
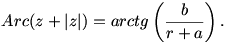
Az
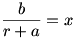
helyettesítéssel
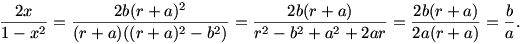
Tehát
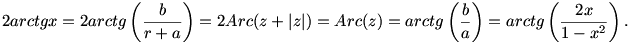
|
| Előzmény: [73] Csizmadia Gábor, 2004-02-16 21:35:35 |
|
| [73] Csizmadia Gábor | 2004-02-16 21:35:35 |
 Bocsánatot kell kérnem, ezt nem ide kellett volna beraknom, mert így a feladat egy kicsit egyszerű. Egy bonyolultabb (de valószínűleg az ide járók többsége által ismert) feladat "melléktermékeként" jött ki ez a tétel, és nem gondoltam bele, hogy ez annál sokkal egyszerűbb úton is bizonyítható.
|
| Előzmény: [72] Csizmadia Gábor, 2004-02-16 18:25:19 |
|
| [72] Csizmadia Gábor | 2004-02-16 18:25:19 |
 Szerintem ez a feladat (mármint maga a tény, és a bizonyítása is) nagyon szép:
Bizonyítsd be, hogy x (-1;1)-re érvényes az alábbi összefüggés: (-1;1)-re érvényes az alábbi összefüggés:
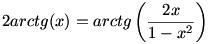
Üdv: Csizmadia Gábor
|
|
| [70] Hajba Károly | 2004-02-12 09:28:28 |
 Kedves gubbubu!
Fáradozásodat én is köszönöm, de az egészséged fontosabb, kúráld ki magad előbb. Addig is megleszünk a megoldás nélkül, mint ahogy eddig is tudtunk élni nélküle. Legalább arra inspirál, hogy újabb ötletek fel- és elvetésével tovább gondolkodjunk a problémán.
Ha lesz egy kis időm, beírom az eddigi kutatásaim eredményeit egy kis kritikára.
HK
|
| Előzmény: [68] Gubbubu, 2004-02-11 18:54:04 |
|
| [69] lorantfy | 2004-02-12 07:46:02 |
 Kedves Gubbubu!
Javulást kívánok Neked! Remélem végülis sikerrel jársz a keresésben, mert már nagyon fúrja az oldalam a kiváncsiság! Én is próbálkozom matematikus ismerőseim körében.
|
| Előzmény: [68] Gubbubu, 2004-02-11 18:54:04 |
|
| [68] Gubbubu | 2004-02-11 18:54:04 |
 Kedves Onogur!
Sajnos, eddigi kutatásaim jobbára negatív eredménnyel jártak, még van egy-két tippem, hol járjak utána, de lehetséges, hogy Magyarországon vagy legalábbis Budapesten vagy legalábbis az ELTÉ-n nincs meg az Erdős-Graham négyzetpakolásos cikk példánya. Most tartok néhány nap szünetet, mivel egy hete már hogy elkapott az "infulenzia" (szerencsére úgy látszik, nem a madárinfluenza, mivel még úgy-ahogy élek), jövő héten még elmegyek egy-két helyre ez ügyben, de lehet, hogy önerőből kell megismételnünk Erdős és Graham bravúrját.
Üdv: G.
|
|
| [67] Zormac | 2004-02-09 15:59:23 |
 Sziasztok,
ez biztos lerágott csont, de mégsem igazán leltem rá a weben a megoldás(ok)ra...
Szóval a probléma azt hiszem már annyiból is ismert, hogy "Szindbád és a nők". Azért leírom:
Szindbád feleséget akar magának választani 100 adott hölgy közül. A folyamat a következő: egymás után elvonulnak előtte a hölgyek (libasorban :-), és Szindbád tetszőleges pillanatban azt mondhatja, rámutatva az épp színe előtt álló hölgyre, hogy "őt akarom!". Ha egy hölgyet nem választott ki, az elment örökre, később már nem térhet vissza rá. Miután választott, a hátralevőket már nem nézi meg (bár ez nem lényeges).
Főhősünk nyilván minél jobb nőt akar, ámde ez is legalább kétféleképp fogalmazható meg:
1) Minden hölgy "szépsége" leírható egy tetszésindexszel (mint számmal, mondjuk 0 és 10 között) és Szindbád maximalizálni akarja ezt a bizonyos számot.
2) Szindbád minél nagyobb eséllyel A LEGSZEBB nőt akarja (speciális esete az előzőnek, ha mondjuk egy kivétellel mindegyik tetszésindex 0).
A második esetre közszájon forog a következő eljárás (azt hiszem, M-stratégia a neve): az első M hölgyet biztosan nem fogja kiválasztani, majd a maradékból kiválasztja az elsőt, aki az első M mindegyikénél szebb; ha nincs ilyen, kiválasztja az utolsót (és boldogtalan lesz).
Tehát a feladatok:
a) Határozzuk meg M azon értékét, amelyre a legnagyobb eséllyel válaszja ki a legszebb hölgyet (ez emlékeim szerint nem túl nehéz, viszont az eredmény "szép").
b) Igaz-e, hogy az M-stratégia, mint módszer, valóban helyes? Azaz, van-e más stratégia, amely az a) részben adódó valószínűségnél jobbat ad?
c) Vajon mi a helyzet az 1), általánosabb esetben?
z.
ps. aki mondjuk mostanság próbál nagyobb lakást, neadjisten házat venni, talán átérzi e feladat Életre kivetített mondanivalóját :-)
|
|
| [66] Csimby | 2004-02-04 10:59:04 |
 Kedves Onogur!
Szerintem az eddig talált legkisebb s-ek vannak fönt azon a lapon, de mivel ezeket a dolgokat nehéz bizonyítani (és szerintem ők sem tették meg) lehet, hogy a tiéd jobb...
|
|
| [65] Hajba Károly | 2004-02-04 10:26:31 |
 Kedves Csimby!
Az első linkedbeli méretek az eddig talált legkisebbeket mutatja?
Úgy tűnik, hogy én az 50 kockát el tudom helyezni kisebb helyre is, mint David Cantrell 2002. augusztusi "találása". Épp egy hasonló feladatot barkácsoltam össze, s a megoldást csak tovább kellett finomítani. s=7,620+ helyett s=7,599-, de még át szeretném számolni; sőt az 52-esre van egy teljesen más elosztású is pontosan ugyanakkora méretben.
Mindamellett az a sejtésem, hogy a közel 45 fokos elforgatással 1.000.000,25 alatti méretben újabb elemet nemigen tudunk behelyezni. Itt valami más jellegű csavarásos megoldás jöhet számításba, melyet kisebb méretben még nem lehet alkalmazni, így elképzelni is nagyon nehéz. Néhány elképzelést végigszámoltam, de nem váltak jó elképzelésnek.
HK
|
| Előzmény: [62] Csimby, 2004-02-03 00:14:51 |
|
| [64] Hajba Károly | 2004-02-03 13:54:45 |
 Kedves Csimby!
Kösz a címeket. A másodikra el is kalandoztam, s ráleltem egy a GEOMETRIA topikban feltett feladatomra is.
De nagyon érdekes az n egységkör ill. egységnégyzet elhelyezéséhez szükséges legkisebb négyzetek keresése is.
De hát hol van ez még a billiótól? :o)
HK
|
| Előzmény: [62] Csimby, 2004-02-03 00:14:51 |
|




 n+m-2
n+m-2  2, akkor S<=m+n-d-1
2, akkor S<=m+n-d-1 



 (-1;1)-re érvényes az alábbi összefüggés:
(-1;1)-re érvényes az alábbi összefüggés: 
