A KöMaL 2017. novemberi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2017. december 11-én LEJÁRT. |
K. 559. Hány olyan legfeljebb hatjegyű szám van, amelyben szerepelnek az 1, 2, 3, 4, 5 számjegyek, mindegyik pontosan egyszer?
(6 pont)
K. 560. Egy vizsgán 30 fő vett részt. Azok, akik megbuktak, 60 pontos átlagot teljesítettek, míg azok, akik átmentek, 84-et. A vizsga átlagpontszáma 80 lett. Hányan mentek át a vizsgán?
(6 pont)
K. 561. Egy regény három kötetben jelent meg. Az oldalakat a három kötetben az első oldaltól az utolsóig folyamatosan számozták meg (1-essel kezdve a számozást). A második kötet 50 oldallal vastagabb, mint az első, a harmadik pedig 1,5-szer olyan vastag, mint a második. A három kötet első oldalszámainak összege 893. Hány oldalas a regény? Hány számjegyet használtak fel az oldalszámozás leírásához?
(6 pont)
K. 562. Alíz elindult vásárolni, csupa 10 és 1000 forintossal (mindegyikből volt nála legalább egy). Elköltötte a pénze felét, majd észrevette, hogy ismét csupa 10 és 1000 forintos van nála. Megszámolta a pénzt, és látta, hogy pont annyi 10 forintosa lett, mint ahány 1000 forintossal elindult, és pontosan feleannyi 1000 forintosa lett, mint amennyi 10 forintossal elindult. Hány forintot költött el Alíz, ha a feltételeknek megfelelő lehető legkevesebb pénzt költötte?
(6 pont)
K. 563. Egy 18 cm oldalú négyzet alakú lemezből kivágtak a négyzet csúcsainál egy-egy 3 cm sugarú kört az ábrának megfelelően. A csúcsoknál keletkező hulladéklemez darabokat eldobták. Mekkora a megmaradt rész területe?
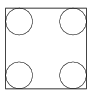
(6 pont)
K. 564. Egy póknak összesen 8 db egyforma zoknit és 8 db egyforma cipőt kell a lábaira felhúzni indulás előtt (minden lábára kell hogy jusson zokni és cipő). Egy adott lábra a zoknit előbb kell felhúzni, mint a cipőt, de nem feltétlenül a cipő felhúzását közvetlenül megelőzően. Hányféle sorrendben veheti fel a pók az összes zoknit és cipőt? (Két felöltözést csak a lábak sorrendje különböztet meg.)
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2017. december 11-én LEJÁRT. |
C. 1441. Egy kávézóban különböző alapanyagokból különböző kávékülönlegességeket készítenek. Tudjuk, hogy az itallapon szereplő bármely kávét kiválasztva pontosan három olyan másik kávét találhatunk, amelynek a kiválasztottal van közös alapanyaga. Azt is tudjuk, hogy ha két kávénak nincs, akkor található hozzájuk egy harmadik, amellyel mindkettőnek van közös alapanyaga. Legfeljebb hány különböző kávékülönlegesség lehet az itallapon?
(5 pont)
C. 1442. Egy háromszög \(\displaystyle a\), \(\displaystyle b\) és \(\displaystyle c\) oldalaira teljesül a következő összefüggés:
\(\displaystyle 1=\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ac}. \)
Igazoljuk, hogy ekkor \(\displaystyle r\cdot R=\frac 12\), ahol \(\displaystyle r\) a háromszög beírható, \(\displaystyle R\) pedig a köré írható körének sugara.
Javasolta: Tatár Zsuzsanna Mária (Felsőgöd)
(5 pont)
C. 1443. Hányféleképpen írható föl \(\displaystyle 2017^3\) egymást követő pozitív páratlan számok összegeként?
Hommer László (Kemence) ötlete alapján
(5 pont)
C. 1444. Oldjuk meg a következő egyenlőtlenséget:
\(\displaystyle x^4-4x^3+8x^2-8x\le 96. \)
(5 pont)
C. 1445. Az ,,Egy angol, aki dombra ment fel, de hegyről jött le'' című filmben egy walesi falu mellett lévő hegyet, miután lemérték a magasságát, a földmérők dombnak minősítettek. A falusiak büszkék voltak a hegyükre, és ebbe nem nyugodtak bele. Elhatározták, hogy 984 lábról 1004 lábra emelik a magasságát. Földet hordanak fel a 82 láb sugarú félgömbnek tekinthető dombtetőre olyan csonkakúp alakban, amelynek alkotója a félgömb érintője, és \(\displaystyle 45^\circ\)-os szöget zár be a vízszintessel. Így a magasság meghaladja majd az 1000 lábat, és a dombot újra hegynek lehet nevezni. Hány köbláb földet kellett felhordaniuk a dombra?
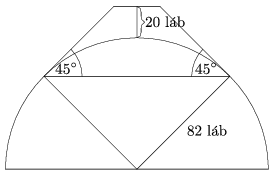
(5 pont)
C. 1446. Az \(\displaystyle ABCD\) paralelogramma belsejében vegyük fel a \(\displaystyle Q\) pontot úgy, hogy \(\displaystyle AQB\sphericalangle+CQD\sphericalangle=180^{\circ}\) legyen. Bizonyítsuk be, hogy \(\displaystyle QBA\sphericalangle=QDA\sphericalangle\) és \(\displaystyle QAD\sphericalangle=QCD\sphericalangle\).
(5 pont)
C. 1447. Mekkora annak a valószínűsége, hogy a VALÓSZÍNŰSÉG, illetve SZÁMÍTÁS szavak mindegyikéből két-két véletlenszerűen választott karaktert véletlenszerűen egymás mellé írva ugyanazt a két ,,szót'' kapjuk?
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2017. december 11-én LEJÁRT. |
B. 4903. Határozzuk meg azokat az \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), \(\displaystyle d\) pozitív egész számokat, amelyekre teljesül, hogy \(\displaystyle abcd-1\mid a+b+c+d\).
Javasolta: Szoldatics József (Budapest)
(4 pont)
B. 4904. Egy \(\displaystyle S\) síkidomnak pontosan kettő szimmetriatengelye van. Mutassuk meg, hogy \(\displaystyle S\) középpontosan is szimmetrikus.
(3 pont)
B. 4905. Legyen \(\displaystyle a_1 \ge a_2 \ge a_3 \ge \ldots \ge a_{2n-1} \ge a_{2n} \ge 0\), illetve \(\displaystyle \sum\limits_{i=1}^{2n} a_i = 1\). Igazoljuk, hogy
\(\displaystyle a_1 a_2 + 3 a_3 a_4 + 5 a_5 a_6 + \ldots + (2n-1) a_{2n-1} a_{2n} \le \frac{1}{4}. \)
Mikor teljesül egyenlőség?
(4 pont)
B. 4906. Az \(\displaystyle ABCD\) konvex négyszög \(\displaystyle BC\) és \(\displaystyle CD\) oldalainak felezőpontja rendre \(\displaystyle E\) és \(\displaystyle F\). Az \(\displaystyle AE\), \(\displaystyle EF\) és \(\displaystyle AF\) szakaszok a négyszöget négy olyan háromszögre bontják, melyek területeinek mérőszáma négy egymást követő egész szám. Legfeljebb mekkora lehet az \(\displaystyle ABD\) háromszög területe?
Javasolta: Róka Sándor (Nyíregyháza)
(5 pont)
B. 4907. Bizonyítsuk be, hogy egy \(\displaystyle a\times b\) méretű téglalapon legfeljebb \(\displaystyle [a] \cdot [b]\) darab olyan \(\displaystyle 1\times 1\)-es négyzet helyezhető el átfedés nélkül, melyek oldalai párhuzamosak a téglalap oldalaival (ahol \(\displaystyle [x]\) az \(\displaystyle x\) szám egész részét jelenti).
(5 pont)
B. 4908. Legyen \(\displaystyle C\) az \(\displaystyle AB\) átmérőjű körvonal tetszőleges pontja. A \(\displaystyle C\) pont merőleges vetülete az \(\displaystyle AB\) szakaszra legyen \(\displaystyle T\). Rajzoljuk meg a \(\displaystyle C\) középpontú, \(\displaystyle T\)-n átmenő kört és a két kör metszéspontjai legyenek \(\displaystyle P\) és \(\displaystyle Q\). Bizonyítsuk be, hogy a \(\displaystyle PQ\) egyenes felezi a \(\displaystyle CT\) szakaszt.
(Kvant)
(4 pont)
B. 4909. Adjuk meg az összes olyan \(\displaystyle f\colon \mathbb{R}\to\mathbb{R}\) függvényt, amely minden \(\displaystyle x\ne0\) és \(\displaystyle y\) esetén kielégíti az alábbi egyenletet:
\(\displaystyle x \cdot f(y) - y \cdot f(x) = f\left(\frac{y}{x}\right). \)
(Kvant)
(6 pont)
B. 4910. Az \(\displaystyle ABCD\) négyzet oldalegyenesein vegyük fel a \(\displaystyle P\), \(\displaystyle Q\), \(\displaystyle R\) és \(\displaystyle S\) pontokat az ábra szerint úgy, hogy \(\displaystyle AP=BQ=CR=DS\). Az \(\displaystyle AB\) oldal tetszőleges belső \(\displaystyle X\) pontjából kiindulva a \(\displaystyle PX\) egyenes messe \(\displaystyle BC\) egyenesét \(\displaystyle Y\)-ban, \(\displaystyle QY\) messe \(\displaystyle CD\) egyenesét \(\displaystyle Z\)-ben, \(\displaystyle RZ\) a \(\displaystyle DA\) egyenest \(\displaystyle V\)-ben, végül \(\displaystyle SV\) az \(\displaystyle AB\) egyenest \(\displaystyle X'\)-ben. Bizonyítsuk be hogy ha \(\displaystyle X'\) és \(\displaystyle X\) egybeesnek, akkor \(\displaystyle XYZV\) négyzet.
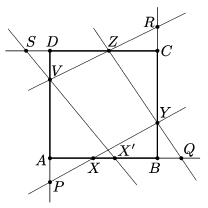
(5 pont)
B. 4911. Egy \(\displaystyle 8\times 8\)-as sakktáblára bábukat helyeztünk úgy, hogy minden sorba és minden oszlopba is páratlan számú bábu került. Bizonyítsuk be, hogy a sötét mezőkön összesen páros sok bábu áll.
(5 pont)
 |
A-jelű feladatokA beküldési határidő 2017. december 11-én LEJÁRT. |
A. 707. \(\displaystyle 100\) betyár áll a hortobágyi síkságon. Mindegyik illető egy \(\displaystyle 100^\circ\)-os szögtartományt lát. Az összes betyár felírja egy-egy papírra, hogy hány másik betyárt lát, majd mi összeadjuk ezt a \(\displaystyle 100\) számot. Mi a lehető legnagyobb összeg, amit ily módon kaphatunk?
(5 pont)
A. 708. Legyen \(\displaystyle S\) racionális számokból álló véges halmaz. Minden \(\displaystyle k\) pozitív egészre legyen \(\displaystyle b_k=0\), ha választható \(\displaystyle k\) darab (nem feltétlenül különböző) \(\displaystyle S\)-beli szám, melyek összege \(\displaystyle 0\), és \(\displaystyle b_k=1\) egyébként. Mutassuk meg, hogy a \(\displaystyle 0{,}b_1b_2b_3\dots\) kettedestört racionális szám. Igaz marad-e az állítás, ha \(\displaystyle S\)-ről nem kötjük ki, hogy véges?
(5 pont)
A. 709. Legyen \(\displaystyle a>0\) valós szám. Határozzuk meg azt a legkisebb \(\displaystyle C_a\) számot, amire a
\(\displaystyle C_a\sum_{k=1}^n \frac1{x_k-x_{k-1}} >\sum_{k=1}^n \frac{k+a}{x_k} \)
egyenlőtlenség teljesül tetszőleges \(\displaystyle n\) pozitív egész és \(\displaystyle 0=x_0<x_1<\ldots<x_n\) valós számok esetén.
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

