A KöMaL 2012. szeptemberi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2012. október 10-én LEJÁRT. |
K. 337. Hány darab 45-tel osztható alakú ötjegyű szám van, ahol a, b és c különböző számjegyeket jelöl?
(6 pont)
K. 338. A háromszög hat szögfelezője (3 külső, 3 belső) közül melyik kettő lehet merőleges egymásra?
(6 pont)
K. 339. Egy teniszklub férfi versenyzőinek 2/3-a indul el a klub női versenyzői közül valakivel vegyespárosban, a többiek csak egyéniben, míg a nők 3/8-a indul valamelyik férfival vegyespárosban, a többiek csak egyéniben. A klub versenyzőinek hányad része indul csak egyéniben?
(6 pont)
K. 340. Fehér színű kis kockákból építünk egy nagyobb kockát, majd befestjük a nagy kocka oldallapjait kékre. Ezután szétszedjük a nagy kockát a kisebb kockákra. Milyen méretű volt a nagy kocka, ha a kis kockák között ugyanannyi páratlan számú kék lappal rendelkező kis kocka van, mint amennyi páros kék lappal rendelkező?
(6 pont)
K. 341. Négy, egységnyi oldalú egybevágó négyzetet egységnyi szélességű folyosók választanak el egymástól, az ábrának megfelelően. Keressük meg az A-ból B-be vezető legrövidebb utat, ami érinti az összes négyzetet! (Az út során a négyzetek belsejébe nem mehetünk be.)

(6 pont)
K. 342. Az ábrán látható ABC háromszög szabályos, AP az A-nál levő belső szög felezője. Bizonyítsuk be, hogy AP=BP+PC.
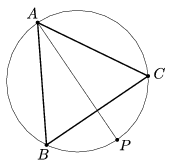
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2012. október 10-én LEJÁRT. |
C. 1130. Mutassuk meg, hogy a négyzetszámok utolsó két számjegye nem lehet egyszerre páratlan.
(5 pont)
C. 1131. Igazoljuk, hogy ha az ABCD konvex négyszögben , továbbá A-nál és B-nél hegyesszög van, akkor
AC2+BD2=AD2+BC2+2.AB.CD.
(5 pont)
C. 1132. Melyik nagyobb az
törtek közül?
(5 pont)
C. 1133. Egy természetes szám hatodik hatványának számjegyei nagyság szerint rendezve a következők: 0, 2, 3, 4, 4, 7, 8, 8, 9. Melyik ez a szám?
(5 pont)
C. 1134. Egy egyenlő szárú trapéz egyik alapja háromszor, a másik kétszer akkora, mint a trapéz magassága. A trapézt az egyik szárával párhuzamos egyenessel egy paralelogrammára és egy egyenlő szárú háromszögre bontjuk, majd megrajzoljuk a trapéz és a paralelogramma átlóit. Bizonyítsuk be, hogy az átlók által határolt háromszög területe a trapéz területének 25-öd része.
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2012. október 10-én LEJÁRT. |
B. 4462. Egy doboz paprikásszalámis és egy doboz medvehagymás, nyolccikkelyes Maci-sajtot kiborítunk az asztalra, majd a 16 kis sajtot (címkéjükkel felfelé) visszatesszük a dobozokba. Hányféleképpen tehetjük ezt meg, ha a forgatással egymásba vihető elrendezéseket nem tekintjük különbözőnek, a két dobozt viszont megkülönböztetjük egymástól?
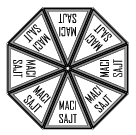
Javasolta: Koncz Levente (Budapest)
(4 pont)
B. 4463. A Négyszögletű Kerek Erdő fái egy szabályos háromszögrács rácspontjain állnak. El lehet-e keríteni az erdőből egy téglalap alakú részt úgy, hogy a téglalap csúcsai rácspontok legyenek, és a téglalap határán ugyanannyi rácspont legyen, mint a belsejében?
(4 pont)
B. 4464. Határozzuk meg az n darab 9-esből álló szám köbében a számjegyek összegét.
(3 pont)
B. 4465. Az A0A10 szakaszt felosztottuk 10 egyenlő részre. Az osztópontok rendre . Az A8A10 szakaszra emelt szabályos háromszög harmadik csúcsa legyen B. Mutassuk meg, hogy
Javasolta: Miklós Szilárd (Herceghalom)
(4 pont)
B. 4466. Van-e olyan pozitív n egész szám, amelyre a
(4n2-1)x2-4n2x+n2=0
egyenlet mindkét gyöke véges tizedestört alakban írható fel?
(3 pont)
B. 4467. Oldjuk meg a
egyenletet.
(5 pont)
B. 4468. Adott két körlemez, melyeknek nincs közös pontja. A körök középpontjait összekötő szakasz, mint átmérő fölé rajzolt kör a két közös külső érintőt két-két pontban metszi. Bizonyítsuk be, hogy ezen négy pont által meghatározott négyszög átlói a körök közös belső érintői.
Javasolta: Gedeon Veronika (Budapest)
(5 pont)
B. 4469. Az ABC háromszög belső szögfelezőinek a szemközti oldalakkal vett metszéspontjai A1, B1, C1. Bizonyítsuk be, hogy az A1B1C1 háromszög területe nem lehet nagyobb az ABC háromszög területének negyedrészénél.
(5 pont)
B. 4470. Az asztalon álló ABCDEFGH kocka három függőleges élét a K, L és M pontok rendre 1:2, 1:3 és 1:4 arányban osztják az ábra szerint. A KLM sík a kockát két részre vágja. Mekkora a két rész térfogatának aránya?
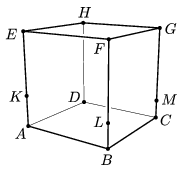
(5 pont)
B. 4471. Melyek azok az egész együtthatós polinomfüggvények, amelyek minden Fibonacci-számhoz pozitív prímszámot rendelnek? (A Fibonacci-számok egy rekurzív sorozat elemei: F0=0, F1=1; n>1-re pedig Fn=Fn-1+Fn-2.)
(6 pont)
 |
A-jelű feladatokA beküldési határidő 2012. október 10-én LEJÁRT. |
A. 566. (a) Bizonyítsuk be, hogy ha n 2, és az
2, és az pozitív valós számok szorzata 1, akkor
(b) Mutassunk példát olyan n 2 egészre és
2 egészre és pozitív valós számokra, amelyek szorzata 1, és
(5 pont)
A. 567. (a) Határozzuk meg az összes olyan, relatív prím pozitív egész a, b számokból álló (a,b) számpárt, amelyre a2-3 osztható b-vel, és b2-3 osztható a-val.
(b) Határozzuk meg az összes olyan, relatív prím pozitív egész a,b számokból álló (a,b) számpárt, amelyre a2-5 osztható b-vel, és b2-5 osztható a-val.
Javasolta: Pelikán József (Budapest)
(5 pont)
A. 568. Adott az ABC háromszög, és a beírt körének középpontján átmenő  egyenes. Jelölje A', B', illetve C' az A, a B, illetve a C pont
egyenes. Jelölje A', B', illetve C' az A, a B, illetve a C pont  -re vonatkozó tükörképét. Legyen az A', B' és C' pontokon át
-re vonatkozó tükörképét. Legyen az A', B' és C' pontokon át  -lel húzott párhuzamosok metszéspontja a BC, CA és AB egyenesekkel rendre P, Q, illetve R. Bizonyítsuk be, hogy a P, Q, R pontok egy egyenesen vannak, és ez az egyenes érinti a beírt kört.
-lel húzott párhuzamosok metszéspontja a BC, CA és AB egyenesekkel rendre P, Q, illetve R. Bizonyítsuk be, hogy a P, Q, R pontok egy egyenesen vannak, és ez az egyenes érinti a beírt kört.
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

