| [1233] hobbymatekos | 2006-04-06 22:25:57 |
 Sziasztok Valahogy úgy érzem, a határozott integrálok nem igazán érdekesek, mint számértékek. Hiszen azt manapság könnyedén numerikus módszerekkel a szükséges pontosságig meg tudjuk határozni. Tanulságosabb az integrál létezése bizonyitása és a primitiv fv. meghatározása (hacsak zárt alakban megadható.) 222.feladat nagyon "szép".
228. feladat: a 222. feladat Riemann-Stieltjes integrálként
|
|
|
|
| [1230] Lóczi Lajos | 2006-04-06 12:39:21 |
 A megoldás (ha létezik, a konvergenciát nem ellenőriztem) csak 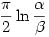 lehet. lehet.
(Utólag a Gyemidovics-példatárban megkeresve ez a 3792-es feladat, és ő Frullani-formulának hívja az általánosítást.)
|
| Előzmény: [1229] nadorp, 2006-04-06 11:33:45 |
|
| [1229] nadorp | 2006-04-06 11:33:45 |
 Erről jutott eszembe a következő.
227.feladat. Adott pozitív  , , esetén határozzuk meg az esetén határozzuk meg az
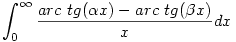
integrál értékét. ( A példa még tovább ragozható, az arc tg függvény helyett bizonyos differenciálható f függvényeket véve. A 225. feladat is visszavezethető ilyen típusú integrálra )
|
| Előzmény: [1228] Lóczi Lajos, 2006-04-05 21:12:15 |
|
| [1228] Lóczi Lajos | 2006-04-05 21:12:15 |
 226. feladat. Adott nemnegatív  esetén határozzuk meg az esetén határozzuk meg az
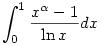
integrál értékét.
|
|
|
|
|
| [1224] hobbymatekos | 2006-04-02 16:56:40 |
 Sziasztok
röviden 1203, 1210, 1213,1214 re:
Azt kell belátni,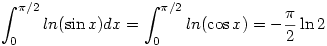
|
|
| [1223] Káli gúla | 2006-03-30 00:29:20 |
 Második megoldás: Az 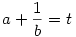 -t átírjuk -t átírjuk 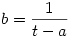 alakba. Ugyanígy alakba. Ugyanígy 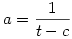 és és  . Ezeket az elsőbe beírva azt kapjuk, hogy . Ezeket az elsőbe beírva azt kapjuk, hogy 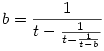 . .
Másik kiindulást választva ugyanezt kapnánk a-ra is és c-re is. Ezeket olvashatjuk úgy, hogy az 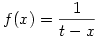 függvény harmadik iteráltjának három különböző fixpontja van. Mivel ez egy tört-lineáris függvény, ez csak úgy lehet, ha minden x-re f(f(f(x)))=x. Ebből azt kapjuk, hogy függvény harmadik iteráltjának három különböző fixpontja van. Mivel ez egy tört-lineáris függvény, ez csak úgy lehet, ha minden x-re f(f(f(x)))=x. Ebből azt kapjuk, hogy 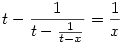 . Az x=0-nál nézve a bal oldalon is a tört nevezőjének 0-nak kell lenni, azaz t=1/t. Tehát t= . Az x=0-nál nézve a bal oldalon is a tört nevezőjének 0-nak kell lenni, azaz t=1/t. Tehát t= 1. Innen már egyszerű. Feltehetjük, hogy t pozitív (ha nem, akkor mindent a (-1)-szeresére cserélünk), tehát t=1. Vegyük pl. a két a-t tartalmazó eredeti egyenletet, szorozzuk a-val a c+1/a=1 mindkét oldalát: 1=a-ac, és ezt írjuk be a másikba: a+1/b=1=a-ac, ami átrendezve: 1 = -abc. 1. Innen már egyszerű. Feltehetjük, hogy t pozitív (ha nem, akkor mindent a (-1)-szeresére cserélünk), tehát t=1. Vegyük pl. a két a-t tartalmazó eredeti egyenletet, szorozzuk a-val a c+1/a=1 mindkét oldalát: 1=a-ac, és ezt írjuk be a másikba: a+1/b=1=a-ac, ami átrendezve: 1 = -abc.
|
| Előzmény: [1221] [evilcman], 2006-03-28 13:17:21 |
|
| [1222] Lóczi Lajos | 2006-03-29 00:54:17 |
 Egyszerűen adódik, hogy a=b-1/b+1/c=1/(b+1/c-c). Ezt tovább helyettesítve, valamint felhasználva az
(b-1/b+1/c)(b+1/c-c)-1=(b-c)(1-c+bc)(1+c+bc)/(bc2)
azonosságot b c figyelembevételével kapjuk, hogy b=(-1-c)/c vagy b=(-1+c)/c. Ki van tehát fejezve a és b mindegyike c-vel; mindkét esetben egyszerűen ellenőrizhető, hogy a+1/b=-abc c figyelembevételével kapjuk, hogy b=(-1-c)/c vagy b=(-1+c)/c. Ki van tehát fejezve a és b mindegyike c-vel; mindkét esetben egyszerűen ellenőrizhető, hogy a+1/b=-abc {-1,+1}. {-1,+1}.
|
| Előzmény: [1221] [evilcman], 2006-03-28 13:17:21 |
|
| [1221] [evilcman] | 2006-03-28 13:17:21 |
 225. feladat Az a,b,c különböző valós számokról tudjuk, hogy 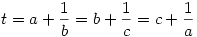 Bb.: t=-abc Bb.: t=-abc
|
|
| [1220] Káli gúla | 2006-03-23 18:27:56 |
 Szia. Elindulhatsz úgy is, hogy a kitevőbe írod a két kifejezést (a logaritmus oda való):
10lg15.lg15=15lg15=1,5lg15.10lg15=1,5lg15.15>1,5*15>22,5
10lg22=22
Tehát az első a nagyobb (mert 10A>10B-ből mindig következik, hogy A>B).
|
| Előzmény: [1216] phantom_of_the_opera, 2006-03-22 15:31:47 |
|
|
|
|
| [1216] phantom_of_the_opera | 2006-03-22 15:31:47 |
 Sziaszok!
Van itt egy feladat amit órán nem nagyon tudtunk megoldani (a tanárral egyetemben). Hátha nektek sikerül.
Melyik a nagyobb (számológép nélkül)?
(lg(15))a négyzeten vagy lg22
UI.: megmondaná valaki hogy miért nem lehet hatványkaraktert meg aláhúzásjelet írni a fórumba? Előre is köszi O.F.
|
|
| [1215] 2501 | 2006-03-22 03:50:31 |
 Ha k=1-et k=0-ra javitod (kulonben mar n=1-re sem teljesul), es a 3-as helyebe (1+2)-t irsz, akkor a binomialis tetelbol kovetkezik az allitas. :)
|
| Előzmény: [1214] Mumin, 2006-03-22 00:24:55 |
|
|
| [1213] nadorp | 2006-03-21 20:09:06 |
 Szerintem a példát az összes hozzászólásával együtt át kéne tenni a "Nehezebb matematikai problémák" közé ( Géza légy szíves ), de azért itt válaszolok, hogy egyben legyen.
Tekintsük az 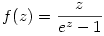 komplex függvényt. Integráljuk a (0,0),(R,0),(R,i komplex függvényt. Integráljuk a (0,0),(R,0),(R,i ),(0,i ),(0,i ) (R>0) téglalap kerületén. A téglalap határán és belsején a függvénynek nincs pólusa ( a 0 sem pólus, mert ott folytonossá tehető), ezért a Cauchy integráltétel miatt az integrál 0. Ha most R ) (R>0) téglalap kerületén. A téglalap határán és belsején a függvénynek nincs pólusa ( a 0 sem pólus, mert ott folytonossá tehető), ezért a Cauchy integráltétel miatt az integrál 0. Ha most R  , akkor az (R,0),(R,i , akkor az (R,0),(R,i ) oldalon vett integrál tart 0-ba (itt felhasználjuk a komplex integrálra érvényes, G görbén vett ) oldalon vett integrál tart 0-ba (itt felhasználjuk a komplex integrálra érvényes, G görbén vett 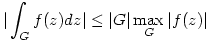 összefüggést). Ha a valós és képzetes részt szétválasztjuk - mindkettő 0 kell hogy legyen -, akkor a képzetes rész éppen összefüggést). Ha a valós és képzetes részt szétválasztjuk - mindkettő 0 kell hogy legyen -, akkor a képzetes rész éppen 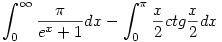 lesz. "Melléktermékként" a valós részből adódik, hogy lesz. "Melléktermékként" a valós részből adódik, hogy
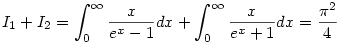 . Mivel pedig . Mivel pedig
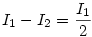 , ezért , ezért 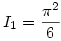 . .
Az pedig ismert, hogy 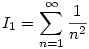
|
| Előzmény: [1212] Lóczi Lajos, 2006-03-20 21:33:00 |
|
| [1212] Lóczi Lajos | 2006-03-20 21:33:00 |
 Hm, köszönöm a javaslatot, erre eddig nem is gondoltam. Tehát parciális integrálással átírjuk (közben a kiintegrált részben limeszt képzünk, ami ugye 0*végtelen-típus), és marad a kotangenses rész. De ezzel mit csinálsz, milyen integrációs utat választasz?
(Én tegnap László példájánál is hasonló "komplex" utat követtem, de sehogyan sem jött ki eleinte a numerikusan megsejtett  2/4, aztán jöttem csak rá, hogy a transzformációm után benne maradó komplex arkusz-tangens függvény nem is analitikus a felső félsíkon -- az i-nél szingularitása van, de ez sem segített, mert a reziduuma nulla volt, és csak legvégül jöttem rá, hogy van egy "branch-cut" bemetszése is, ami i-től felfelé halad a képzetes tengelyen...kellemetlen mellékvágány volt.) 2/4, aztán jöttem csak rá, hogy a transzformációm után benne maradó komplex arkusz-tangens függvény nem is analitikus a felső félsíkon -- az i-nél szingularitása van, de ez sem segített, mert a reziduuma nulla volt, és csak legvégül jöttem rá, hogy van egy "branch-cut" bemetszése is, ami i-től felfelé halad a képzetes tengelyen...kellemetlen mellékvágány volt.)
Az elemi trükkös megoldás lényege a logaritmusos feladatban pl. az, hogy 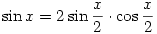 , majd használunk egy szimmetria-érvelést és egy lineáris helyettesítést az integrálban, amiből egy integrálegyenlet adódik a keresett integrálra, és az jön ki, amit írtál. , majd használunk egy szimmetria-érvelést és egy lineáris helyettesítést az integrálban, amiből egy integrálegyenlet adódik a keresett integrálra, és az jön ki, amit írtál.
A vonalintegrálos megoldásod vázlatára kíváncsi vagyok.
|
| Előzmény: [1209] nadorp, 2006-03-20 14:36:24 |
|
| [1211] nadorp | 2006-03-20 18:21:05 |
 Kedves Iván88 !
Van egy kis hiányosság. Egyrészt a p=7 nem az egyedüli megoldás. Másrészt a (2) lépésben, nem p=x, hanem p|x következik. Harmadrészt nem egyértelmű, hogy a 7p p3 milyen modulusra vonatkozik. p3 milyen modulusra vonatkozik.
|
| Előzmény: [1210] Iván88, 2006-03-20 17:02:37 |
|
| [1210] Iván88 | 2006-03-20 17:02:37 |
 Kedves László!
Tetszik a feledat. A kis-Fermat tétel (ha p prím, akkor minden c egészre cp-c osztható p-vel) miatt 7x osztható p-vel.
Ez kétféleképpen lehet.
(1) p=7, ekkor x=361
(2) x=p, ekkor
3p-3=7p-p3
Mivel 7p p3, így p=3. p3, így p=3.
Ez viszont nem megoldás, tehát p=7 és x=361
|
| Előzmény: [1202] lorantfy, 2006-03-19 15:55:20 |
|
|




 ,
, esetén határozzuk meg az
esetén határozzuk meg az 

 1. Innen már egyszerű. Feltehetjük, hogy t pozitív (ha nem, akkor mindent a (-1)-szeresére cserélünk), tehát t=1. Vegyük pl. a két a-t tartalmazó eredeti egyenletet, szorozzuk a-val a c+1/a=1 mindkét oldalát: 1=a-ac, és ezt írjuk be a másikba: a+1/b=1=a-ac, ami átrendezve: 1 = -abc.
1. Innen már egyszerű. Feltehetjük, hogy t pozitív (ha nem, akkor mindent a (-1)-szeresére cserélünk), tehát t=1. Vegyük pl. a két a-t tartalmazó eredeti egyenletet, szorozzuk a-val a c+1/a=1 mindkét oldalát: 1=a-ac, és ezt írjuk be a másikba: a+1/b=1=a-ac, ami átrendezve: 1 = -abc.  c figyelembevételével kapjuk, hogy b=(-1-c)/c vagy b=(-1+c)/c. Ki van tehát fejezve a és b mindegyike c-vel; mindkét esetben egyszerűen ellenőrizhető, hogy a+1/b=-abc
c figyelembevételével kapjuk, hogy b=(-1-c)/c vagy b=(-1+c)/c. Ki van tehát fejezve a és b mindegyike c-vel; mindkét esetben egyszerűen ellenőrizhető, hogy a+1/b=-abc {-1,+1}.
{-1,+1}.



 ),(0,i
),(0,i
 , akkor az (R,0),(R,i
, akkor az (R,0),(R,i p3 milyen modulusra vonatkozik.
p3 milyen modulusra vonatkozik. 