| [244] Sirpi | 2004-02-16 11:07:28 |
 n2+1=2m és m 2 esetén a bal oldal 4-es maradéka 1 vagy 2, a jobb oldalé 0, tehát ilyenkor nincs megoldás. 2 esetén a bal oldal 4-es maradéka 1 vagy 2, a jobb oldalé 0, tehát ilyenkor nincs megoldás.
m=0 esetén n=0, m=1 esetén n= 1 adódik, és ezzel az egyszerü húzással az eredeti feladatot is megoldottuk. 1 adódik, és ezzel az egyszerü húzással az eredeti feladatot is megoldottuk.
S
|
| Előzmény: [238] Zormac, 2004-02-12 16:24:18 |
|
| [242] Lóczi Lajos | 2004-02-13 23:49:10 |
 Kedves Onogur,
ha csak képlet kell, azt könnyű gyártani:) Íme egy, amely megadja az egyenlet megoldását, ha az iteratív módszer már szóba került:
lim(ak),
ahol ak+1=log2(ak2+1), és például a0=4. (A limesz létezik, mert az ak sorozat monoton növő és felülről korlátos.)
|
| Előzmény: [240] Hajba Károly, 2004-02-13 13:27:42 |
|
|
| [240] Hajba Károly | 2004-02-13 13:27:42 |
 Kedves Zormac!
n=4 42+1>24 42+1>24
n=5 52+1<25 52+1<25
Így a (4,5) tartományban van egy megoldás, ezt én iteratív úton meghatároztam [214], továbbá tény, hogy n>5 megoldás már nem létezik, amire hozzászólásodban utaltál. Mi arra is kiváncsiak lettünk volna, hogy ez képlet formájában megadható-e. Eddig erre nem jött válasz, tehát szerintem nem olyan egyszerű a feladat.
HK
|
| Előzmény: [238] Zormac, 2004-02-12 16:24:18 |
|
|
| [238] Zormac | 2004-02-12 16:24:18 |
 A 47. feladat valóban nem kelt el, pedig egyszerű... (az volt, hogy oldjuk meg: n2+1=2n).
Először is n=0 és n=1 megoldások, 2 n n 5 pedig nem megoldások, amint azt könnyű ellenőrizni. Ráadásul n=5-re már igaz, hogy 2n<n2+1 és ennek az öröklődését könnyű belátni nagyobb n-ekre, például azáltal, hogy a 2n sorozat hányados-sorozata nagyobb, mint az n2+1 sorozaté (afféle indukció): 5 pedig nem megoldások, amint azt könnyű ellenőrizni. Ráadásul n=5-re már igaz, hogy 2n<n2+1 és ennek az öröklődését könnyű belátni nagyobb n-ekre, például azáltal, hogy a 2n sorozat hányados-sorozata nagyobb, mint az n2+1 sorozaté (afféle indukció):
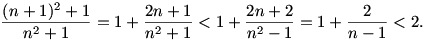
Esetleg az lehetne egy nehezebb feladat, hogy oldjuk meg az alábbit (nem tudom, értelmes feladat-e, csak úgy eszembe jutott, hátha mi lesz :-)
n2+1=2m.
|
|
| [237] lorantfy | 2004-02-12 13:24:38 |
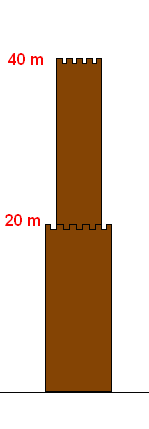
 56.feladat: 40 m magas torony tetejéről kell lejutnunk. Van egy 30 m-es kötelünk, késünk és gyufánk. A kötelet csak 40 m és 20 m magasságban lehet rögzíteni. Leugrani persze semmilyen magasságból sem tanácsos.
(Aki ismeri, ne lője le!)
|
 |
|
| [236] lorantfy | 2004-01-24 17:46:38 |
 A 35. feladat a Cornides István Matematika - Fizika Emlékverseny 1.feladata volt és így szólt:
Határozza meg, mely p valós számokra van az
x3+px2+2px=3p+1
egyenletnek három különböző a, b, c valós gyöke, amelyre ab=c2.
35. faladat megoldása: A három gyök a, b, c tehát a gyöktényezős alak:
(x-a)(x-b)(x-c)=x3-(a+b+c)x2+(ab+ac+bc)x-abc=0
Összehasonlítva ezt az eredeti egyenlettel és alakítgatva:
a+b+c=-p  a+b=-c-p a+b=-c-p
ab+ac+bc=2p  ab+(a+b)c=2p ab+(a+b)c=2p
abc=3p+1 mivel ab=c2  c3=3p+1 c3=3p+1
Második egyenletbe ab és (a+b) értékét beírva:
c2+(-p-c)c=2p  -pc=2p -pc=2p  0=p(c+2) 0=p(c+2)
Tehát p = 0 vagy c=-2
p=0 esetén x3=1 a=1, b=1, c=1 és ab=c2 is teljesül.
Ha c=-2, akkor p = -3, a+b=5, ab=4 és így a2-5a+4=0.
Gyökei: a=1 vagy a=4, amihez b=4 vagy b=1 tartozik.
p= -3 esetén az eredeti egyenlet gyökei valóban 1, 4 és -2.
|
| Előzmény: [233] Hajba Károly, 2004-01-23 11:50:49 |
|
|
| [234] Hajba Károly | 2004-01-23 12:24:42 |
 55. feladat:
Daraboljuk az egységnégyzetet kisebb négyzetekre.
A) Milyen részekre nem lehet feldarabolni?
B) Lehet-e legalább 11 féleképpen feldarabolni 11 részre?
HK
|
|
| [233] Hajba Károly | 2004-01-23 11:50:49 |
 Kedves Topik!
A még meg nem oldott feladatok listája:
3. [3] (félig megoldva!)
12. [60]
35. [148]
40. [180]
44. [199]
47. [204]
54. [229]
Jó gondolkodást a hétvégére :o)
HK
|
|
| [232] Hajba Károly | 2004-01-22 08:21:42 |
 Kedves László!
Tény, hogy hamar lelőttem, de cserében feltettem gyorsan egy másikat. Hasonló feladatokat a GEOMETRIA topikba is raktam, de eddig nem harapot rá senki, pedig lehetne még néhányat feladni. Érdekes - legalábbis számomra - a kitölthetőségi téma.
HK
|
| Előzmény: [229] lorantfy, 2004-01-21 14:32:49 |
|
| [231] Elti | 2004-01-21 17:18:42 |
 Szevasztok, csao! szeretnelek titeket ertesiteni arrol, hogy a trefort.chat.net -en megalakult a KoMaL szoba, szivesen varunk mindenkit, hogy kialakithassunk egy jo kis matekos, fizikas legkort! remelem minnel tobben leszunk! Hello
|
|
| [230] pataki | 2004-01-21 17:00:22 |
 Érdemes megnézni az 1990. évi diákolimpia 3. feladatát.
Ez egyúttal könyvajánlás is: Reiman István - Dobos Sándor: Nemzetközi Matematikai Diákolimpiák 1959 - 2003, Typotex Kiadó
|
| Előzmény: [216] Gubbubu, 2004-01-14 23:50:07 |
|
|
| [228] Hajba Károly | 2004-01-21 14:10:54 |
 Kedves László!
54. feladat:
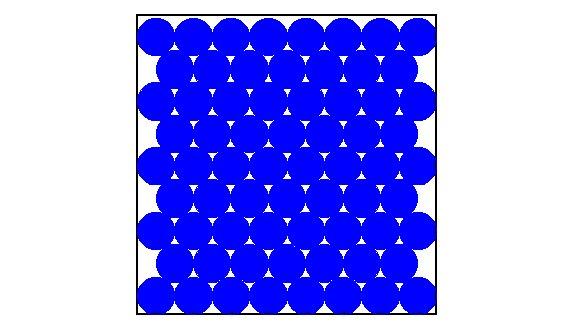
Vegyünk el ebből a 64 golyóból 1 darabot. Mekorra az a legkisebb négyzet alakú keret belső mérete, amibe még bele lehet rakni ezt a 63 darab golyót?
HK
|
| Előzmény: [226] lorantfy, 2004-01-21 13:37:20 |
|
|
| [226] lorantfy | 2004-01-21 13:37:20 |
 53. feladat: Egy 8 egység belső méretű négyzet alakú keretbe belaraktunk 64 db 1 egység átmérőjű fémgolyót. (A golyók egymással és a keret falával érintkeznek)
Hány ugyanilyen golyót tudnál még berakni a keretbe?
|
 |
|
|
| [224] lorantfy | 2004-01-18 21:34:02 |
 Kedves Károly!
Ügyes példák – főleg a gyujtózsinóros!
50. feladat megoldása: Elég reménytelennek tűnik a megoldás, mivel véletlenszerűen égnek a zsinórok nem darabolhatjuk őket. Akkor mit lehet tenni? Ami biztos, hogy, ha mondjuk már fél órája ég a zsinór akkor a hátralévő zsinórdarab is fél óráig ég még. Tehát ha mindkét végét meggyujtjuk az egyik zsinórnak, akkor 1/2 óra alatt ér össze a láng.
Ha a másik zsinórt is meggyujtjuk az első két végének meggyujtásával egyidőben, akkor amikor az elsőn a láng összeér a másik zsinórból még pont félórányi van hátra. Ekkor meggyujtjuk a második zsinór másik végét is és a két láng pontosan 1/4 óra múlva ér össze. Tehát lemértük a 3/4 órát.
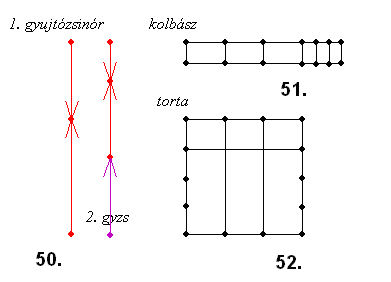
51. feladat megoldása: A kolbászt 3 vágással felvágjuk 4 egyenlő részre, majd az egyik részt továbi két vágással harmadoljuk.
52. feladat megoldása: A tortát 2 párhuzamos vágással harmadoljuk, majd 1 merőleges vágással elvágjuk az 1/4 részénél.
|
 |
| Előzmény: [223] Hajba Károly, 2004-01-17 01:11:18 |
|
| [223] Hajba Károly | 2004-01-17 01:11:18 |
 50. feladat:
Adott két kanóc, melyek egyenként pontosan 1-1 óra alatt égnek le, de az égési sebességük véletlenszerűen változó. (Tehát a fele nem feltétlen fél óra alatt ég le.)
Hogyan tudunk ezen kanócok segítségével 0,75 órát lemérni?
51. feladat:
Hogyan lehet egy szál kolbászt 10-nél kevesebb vágással úgy feldarabolni, hogy akár 3, akár 4 egyenlő részre lehessen osztani?
52. feladat:
Hogyan lehet egy négyzet alakú tortát 3 egyenes vágással felszeletelni, hogy akár 3, akár 4 egyenlő részre lehessen osztani?
HK
|
|
| [222] Gubbubu | 2004-01-16 18:32:09 |
 Kedves Onogur!
Semmi baj, úgy sejtettem, hogy az eredeti szövegrészben egy rész véletlenül törlődött (ilyesmi sokszor előfordul, kétszer át szoktam nézni, mit írok, de mindig kerül hiba bele). Az első féle általánosítás így is érthető volt. Persze, megoldani egyiket sem tudom, a numerikus és közelítő módszerek elmélete nemigen megy nekem.
Üdv.: G.
(U.I. Azt hiszem, megoldottam a mágusos feladatot, de még várok egy-két hétig, mielőtt felteszem, hátha más is szeretne még gondolkodni.)
|
| Előzmény: [221] Hajba Károly, 2004-01-16 14:07:52 |
|
| [221] Hajba Károly | 2004-01-16 14:07:52 |
 Kedves gubbubu!
A kétféle általánosítási irány összevonását elkapkodtam. Tehát korrigálva magam:
1. A x2+d=2x egyenlet görbéinek jellegéből adódik, hogy 1, 2 v. 3 megoldás lehetséges, ahol d lehet 0 értékű is, továbbá mely d-re adódik 2 megoldás?
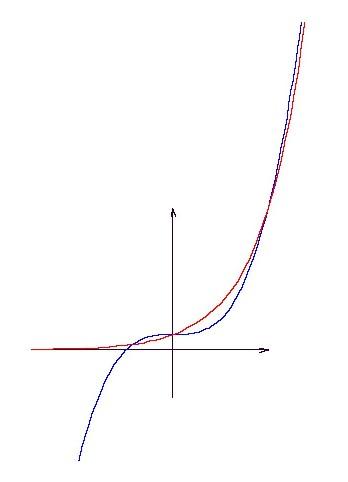
2. A feladaton lehet általánosabban is az an+d=na formában gondolkodni. Pl. x3+1=3x esetet az ábra mutatja. (y harmadával torzítva és ott fenn van még egy metszéspont.) x1 -0,845838;x2=0;x3=2;x4 -0,845838;x2=0;x3=2;x4 3,220644. Így itt 4 metszéspont van. 3,220644. Így itt 4 metszéspont van.
Remélem, most már nem írtam marhaságokat. :o)
HK
|
 |
| Előzmény: [220] Gubbubu, 2004-01-16 00:46:54 |
|
| [220] Gubbubu | 2004-01-16 00:46:54 |
 Üdv, Onogur,
Kösz a kimerítő (de érdekes) magyarázatot, és a történeti kiegészítést! Most már lesz min gondolkodnom a következő kb. 5 évben... Valószínűleg már az sem triviálisan látható be, hogy mindig lf. 3 metszéspont van, mert a "görbék jellege" kifejezés arra utal, hogy minimum differenciálszámítás van a háttérben. Legalábbis ilyentájt, 0:36-kor egyelőre ennyit vagyok képes látni.
Persze ki lehet tűzni a "Nehezebb matematikai problémák" rovatban ezeket az általánosításokat... hátha egyszer valaki megoldja őket... mondjuk valaki, aki "lovaszlaszlo" n.name-mel van bejelentkezve...
Üdv: G.
|
| Előzmény: [219] Hajba Károly, 2004-01-15 09:24:06 |
|
| [219] Hajba Károly | 2004-01-15 09:24:06 |
 Kedves gubbubu!
- A Bezier-görbék és a továbbfejlesztett változatuk a B-spline módszer 30 éve kezdett el terjedni a mérnöki számítógépes formatervezés területén. Lényege, hogy adott pontokkal leírjuk a görbét vagy térbeli felületet és a pontok közötti vonalat ill. felületet súlyozott paraméterfüggvénnyel írjuk le. Lényeges, hogy a pontokban és illeszkedési vonalakban legalább másodrendűen illeszkednek a görbék ill. felületek. A pontokkal, s illeszkedésükkel lehet globális vagy lokálisan változtatni ill. a súlyozás mértékét is lehet szabályozni a modell megjelenésén.
P. Bezier a '70-es évek legelején dolgozta ki e módszert a Renault gépkocsik formatervezésének számítógépes modellezése során, s ezt vették át más mérnöki területek is.
- A felvetetted problémán egyébként már korábban én is gondolkodtam a x2=2x formában. Ennek is két egészértékű megoldása van. Továbbá felvetésed után a következő általánosítások vetődtek fel bennem:
A görbék jellegéből adódik, hogy 1, 2 v. 3 megoldás lehetséges, s általában na+d=an alakú, ahol d lehet 0 értékű is, továbbá a és d függvényében mely d-re adódik 2 megoldás?
HK
|
| Előzmény: [218] Gubbubu, 2004-01-15 00:58:00 |
|



 2 esetén a bal oldal 4-es maradéka 1 vagy 2, a jobb oldalé 0, tehát ilyenkor nincs megoldás.
2 esetén a bal oldal 4-es maradéka 1 vagy 2, a jobb oldalé 0, tehát ilyenkor nincs megoldás.  1 adódik, és ezzel az egyszerü húzással az eredeti feladatot is megoldottuk.
1 adódik, és ezzel az egyszerü húzással az eredeti feladatot is megoldottuk. 


 42+1>24
42+1>24  n
n

 a+b=-c-p
a+b=-c-p



 -0,845838;x2=0;x3=2;x4
-0,845838;x2=0;x3=2;x4