| [3000] Radián | 2009-07-22 19:17:50 |
 Lehet, hogy kicsit elsietem, de nem lehet tudni mikorra lesz meg e probléma megoldása. Kapcsolódó kérdés:
Mely prímeknek van többjegyű palindrom hatványa?(7-nek,11-nek,101-nek van, de vajon rendelkezik e tulajdonsággal még valamelyik másik prím is?)
|
|
| [2999] Radián | 2009-07-22 19:13:37 |
 Csak addig jutottam, hogy 2 hatványai közül csak azok jöhetnek szóba melyek 20-szal való osztási maradéka 1,2,3 v. 16. Gondolom ez a tény semmire se jó de hátha valami csoda folytán valakinek segít:)
|
|
|
| [2997] MTM | 2009-07-19 16:18:36 |
 Üdv!
Van-e 2-nek többjegyű palindromhatványa?
|
|
|
| [2995] sanyi15ka | 2009-06-26 09:43:13 |
 En mashogy oldottam meg, de igy is jo. En inkabb roman modszert hasznaltam, vagyis egy kis rendezessel felirtam 3 egyenlotlenseget es ezek altal bebizonyitottam h csak n=3-ra kompatibilisek az egyenletek es igy megkimeltem magam attol, hogy n=1-t, illetve n=2-t targyaljam.:)
|
| Előzmény: [2994] R.R King, 2009-06-26 08:34:00 |
|
| [2994] R.R King | 2009-06-26 08:34:00 |
 egy pozitív szám és a reciprokának összege legalább 2, így a második egyenletből n legfeljebb 3 lehet.Ha n pl 3 akkor a második egyenlet csak X(i)=1 esetben teljesülhet.Ez teljesíti az első egyenletet is. Ebben az esetben tehát a kérdéses összeg 3. n=1, illetve n=2-tőt rád bízom:)
|
| Előzmény: [2993] sanyi15ka, 2009-06-26 00:32:28 |
|
| [2993] sanyi15ka | 2009-06-26 00:32:28 |
 Udv! 10. vegen megkert minket a matektanarunk, hogy szerkesszunk 2 matek feladatot. Nekem ez lett az egyik. Az e-mail cimemre varom a megoldasokat. Ha lehet akkor a feladatom elemi matekkel legyen megoldva, mert csak jovore, 11-be, tanulok analizist meg felsobb dolgokat es azokat meg nem tudom.
|
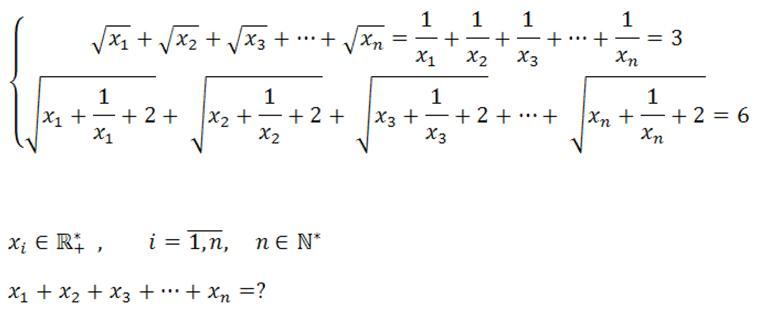 |
|
|
| [2991] m2mm | 2009-06-22 22:08:40 |
 Üdv!
Két idei KöMaL-feladat általánosítása:
Egy májusi feladat:
B. 4185. Mutassuk meg, hogy minden nemnulla polinomnak van olyan nemnulla polinomszorosa, amelyben minden tag kitevője osztható 3-mal.
Ez a (a+b+c)(a2+b2+c2-ab-bc-ca)=a3+b3+c3-3abc azonossággal könnyen kezelhető.
A kérdés: Mely n-ekre igaz az, hogy minden nemnulla polinomnak van olyan nemnulla polinomszorosa, amelyben minden tag kitevője osztható n-nel?
Egy márciusi feladat:
B. 4167. Egy n pozitív egészre jelölje f(n) az n tízes számrendszerbeli alakjának a megfordításával kapható számot. (Tehát f(2500)=52, f(1456)=6541.) Keressük meg azokat a pozitív egész k számokat, amelyekre teljesül, hogy tetszőleges n többszörösükre k az f(n) számnak is osztója.
A kérdés: Mik a keresendő k számok r alapú számrendszerben? (esélyesnek tartom r2-1 osztóit, de nem tudtam bizonyítani)
|
|
|
|
|
| [2987] Lóczi Lajos | 2009-06-21 00:17:51 |
 Az asztroidot egy differenciálegyenlet megoldásaként is megkaphatjuk.
Ha f jelöli a keresett burkológörbét, akkor felírva az "érintőszakaszok pozitív síknegyedbe eső része konstans" feltételt, az alábbi egyenlet adódik:
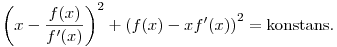
Ezt megoldva (és a triviális eseteket eldobva) éppen az asztroid egyenletét kapjuk.
|
| Előzmény: [2985] HoA, 2009-06-19 15:08:04 |
|
| [2986] leni536 | 2009-06-19 15:52:56 |
 Ennek a burkolónak a neve asztroid. Érdemes megfigyelni, hogy a buszok ajtaja is valahogy hasonlóan nyílik, és mivel az aljukon van egy seprű, ezért a lépcső alján lévő kosznak a burkolója is ugyanez a görbe.
|
|
|
|
| [2983] Alma | 2009-06-18 13:41:26 |
 Látom senki sem írta fel a polárkoordinátás megoldást, és újabb kérdések vetődtek fel, ezért beírom én.
Már az előttem szólók megállapították, hogy a mozgás során szimmetria okokból az eredeti négyzetalak megmarad, csak zsugorodik és elfordul. Jól jellemezhető a rendszer tehát két paraméterrel: az egyik pont középponttól (ez lesz az origó) való r távolságával, ami kezdetben 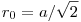 , valamint az origóból a pontba mutató vektor , valamint az origóból a pontba mutató vektor  szögelfordulásával. szögelfordulásával.
Minden pillanatban a pontok sebességvektorának radiális és tangenciális komponense is 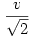 , ami azt jelenti, hogy a következő differenciálegyenleteket írhatjuk fel a sebesség definíciója alapján: , ami azt jelenti, hogy a következő differenciálegyenleteket írhatjuk fel a sebesség definíciója alapján: 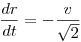 valamint valamint 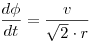 . Az első egyenlet megoldása kezdeti feltétellel: . Az első egyenlet megoldása kezdeti feltétellel:
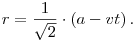
Ebből leolvasható, hogy a pontok 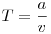 idő mulva találkoznak, vagyis addig a utat tesznek meg. idő mulva találkoznak, vagyis addig a utat tesznek meg.
Ha már eddig leírtam, akkor gyorsan a pályát is levezetem ebből:
A kapott sugár-idő függvényt behelyettesítve a szögre vonatkozó differenciálegyenletre a következőt kapjuk:
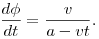
Integrálva az egyenletet, valamint figyelembe véve a kezdeti feltételt 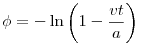 . Az időt kifejezve a pillanatnyi sugárral és behelyettesítve ide megkapjuk a pálya egyenletét: . Az időt kifejezve a pillanatnyi sugárral és behelyettesítve ide megkapjuk a pálya egyenletét:
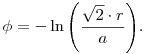
Kicsit szebb alakban:
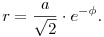
Ez pedig egy logaritmikus spirál.
|
| Előzmény: [2979] Lóczi Lajos, 2009-06-17 22:49:08 |
|
|
|
| [2980] HoA | 2009-06-18 09:53:57 |
 Látszik. Érdemes megfigyelni , hogy [2961] ábráján hogyan változik az időközben teknőcökké előlépett pontok által alkotott négyzet oldalhossza, ha azok  x -et lépnek egymás felé. Különösen hasznos ezt összevetni a [2972]-ben említett háromszöges változat esetével. Szabatos-e az ezekből levezetett eredmény a görbe hosszára azon az alapon, hogy mikorra csökken a futópontok által meghatározott négyzet/háromszög oldalhossza 0-ra? x -et lépnek egymás felé. Különösen hasznos ezt összevetni a [2972]-ben említett háromszöges változat esetével. Szabatos-e az ezekből levezetett eredmény a görbe hosszára azon az alapon, hogy mikorra csökken a futópontok által meghatározott négyzet/háromszög oldalhossza 0-ra?
|
| Előzmény: [2979] Lóczi Lajos, 2009-06-17 22:49:08 |
|
|
|
| [2977] HoA | 2009-06-17 20:20:02 |
 Egy "kapcsolódási pont": Az ábra szimmetrikus az y=x egyenesre, így a keresett függvény saját inverze. Ellenőrizhetjük Ákos megoldását:
y=(1-x2/3)3/2
y2/3=1-x2/3
x2/3=1-y2/3
x=(1-y2/3)3/2
A megoldás tehát akár jó is lehet :-)
|
| Előzmény: [2976] Lóczi Lajos, 2009-06-17 15:33:27 |
|
| [2976] Lóczi Lajos | 2009-06-17 15:33:27 |
 (Persze az egységlétra esetén :)
A feladatot még többféleképp is meg lehet oldani, bizonyára látni fogunk több szép geometriai, illetve differenciálegyenletes kapcsolódási pontot.
|
| Előzmény: [2975] S.Ákos, 2009-06-17 14:47:38 |
|



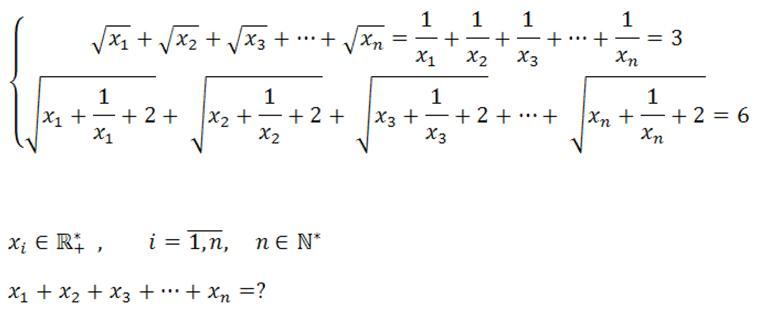





 ;BT=cos2
;BT=cos2