|
|
| [458] hegeduscs | 2008-04-13 11:52:16 |
 Van egy 5-es feladatom: Van egy számsorozatunk: 11,13,15,19,25,35,42 A)Mi a kapcsolat a számok között? B)Folytasd a sort! Üdv, Csabi
|
|
| [457] Valvehead | 2008-04-13 09:51:33 |
 Lehet, hogy tényleg ez a sor a megoldás. Köszönöm szépen. Ezek szerint nem csak én útáltam a "hülye szabályú" kitalálós sorozatokat? Azért volt érdekes ez a kérdés, mert az összes többi feladat nem ütötte meg a versenyszínvonalat.
|
| Előzmény: [456] Róbert Gida, 2008-04-13 02:37:58 |
|
| [456] Róbert Gida | 2008-04-13 02:37:58 |
 Szerintem nézd meg a belinkelt sorozatot, tizedik eleme éppen 2. Valószínű, hogy erre a sorozatra gondoltak, annyira nem elvetemült (bár szinte lehetetlen kitalálni), a sorszáma is roppant alacsony (2963), ez azt jelenti, hogy ez a Sloane sorozatos könyvében is megjelent.
Katonaságnál az alkalmassági teszt (vagy hogyhívják?) volt ilyen, matematika rész csak ilyen *feladatokból* állt egy oldalon minden sorban a megkezdett sorozatot kellett folytatni. Igazolásom nem lévén 3-szor is volt szerencsém kitölteni ugyanazt a tesztet, azt hiszem a végén már majd 100 százalékra, nyelvtani-fizikai rész már nem ment ilyen jól. Bár gondoltam arra is, hogy szándékosan hülyének tettetem magam és elrontom, simán ment volna. Szerencsére megszüntették a sorkatonaságot mire ténylegesen behívtak volna.....
|
| Előzmény: [454] Valvehead, 2008-04-12 23:43:06 |
|
| [455] Káli gúla | 2008-04-12 23:45:04 |
 Hasonló, talán még elvetemültebb a 6,2,5,5,4,5,6,... sorozat, internet nélkül elég reménytelen folytatni. Szintén megtalálható ugyanott: A010371.
|
| Előzmény: [453] Róbert Gida, 2008-04-12 15:31:00 |
|
| [454] Valvehead | 2008-04-12 23:43:06 |
 Na ja, ennyit sem tudok begépelni.. Három válaszlehetőség is van:
a) 2 b) 5 c)7
Jó, attól hogy egy ismeretlen fokszámú polinomnak megadunk véges számú pontját nem lesz határozott. Igazad van, arra gondoltam, hogy legalább 3-adfkú. Én nem tudom megoldani a feladatot, ezért kérek segítséget.
|
| Előzmény: [453] Róbert Gida, 2008-04-12 15:31:00 |
|
| [453] Róbert Gida | 2008-04-12 15:31:00 |
 "Hatodik osztályos versenyfeladat"
A zárt osztályon?
7-ed fokú polinomot illesztve az első 7 elemre és tetszőleges tizedikre bármilyen komplex szám lehet a tizedik tag, ezért sem értelmes a kérdés.
Neil Sloane több, mint 100,000 sorozatát tartalmazó adatbázisában csak egy sorozat kezdődik így: A002963
|
| Előzmény: [452] Valvehead, 2008-04-12 15:19:51 |
|
| [452] Valvehead | 2008-04-12 15:19:51 |
 Első hozzászólás alkalmából üdvözlöm a fórumot! Hatodik osztályos versenyfeladattal nem boldogulok, hátha valaki tud segíteni... Melyik szám lehet a sorozat 10. eleme?
1; 2; 3; 3; 2; 3; 4; ..; ..; ..
Persze, explicit alakban biztos harmadfokú (3db 3-as) meg gondolom van rá egy primitív rekurziós képlet, amitől fogom majd a fejem...
Aki foglalkozik vele, annak előre is köszönöm szépen!
|
|
|
| [450] Róbert Gida | 2008-04-11 17:23:32 |
 Különböző dolgokról beszélsz, páratlan n esetén az, hogy nincs más megoldás csak a triviális y=1, illetve y=n ekvivalens azzal, hogy n-nek nincs más pozitív osztója, azaz n az prím (n>1 fel volt téve). Erre pedig van már gyors egzakt polinomiális teszt, az "AKS test", keress rá az interneten, persze vannak véletlen (nem egzakt) módszerek is. Míg legalább egy y megtalálására nincs gyors módszer, hiszen ez a szám faktorizálásával polinomiálisan ekvivalens probléma, amiről nem tudjuk, hogy gyorsan meg lehet-e csinálni.
|
| Előzmény: [448] csewe, 2008-04-11 15:02:30 |
|
| [449] Sirpi | 2008-04-11 15:41:50 |
 De ez nem segít a szűkítésben, ahogy már írtam...
Megfelelő x, y pár megtalálása egyenértékű azzal, hogy megtalálod azt az y-t, ami osztja n-et.
|
| Előzmény: [448] csewe, 2008-04-11 15:02:30 |
|
| [448] csewe | 2008-04-11 15:02:30 |
 szia Sirpi
addig én is eljutottam,hogy y = 1 , de mint írtam 1 < y
mert igazából az érdekelne hogy van e másik felbontása n -nek mert sok esetben van mégha nem is kapom meg a másik felbontást de el kellene döntenem , hogy létezik e.
egyébként ezek az én agyam szüleményei , a progimhoz kellene. azért ,hogy ne keljen minden értéket végig zongorázni.
|
| Előzmény: [447] Sirpi, 2008-04-11 10:41:55 |
|
| [446] epsilon | 2008-04-11 10:56:21 |
 OK nadorp, kösz, valóban elszámoltam, mert Nekem a tg a 2n-en lett, mert egy sin a négyzeten "bennmaradt" :-( Túl csábító volt az a változócsere, és csodálkoztam is, hogy miért nem jön össze! Üdv: epsilon
|
| Előzmény: [440] nadorp, 2008-04-09 16:14:07 |
|
| [447] Sirpi | 2008-04-11 10:41:55 |
 Figyi, minden feladatod arra megy ki, hogy n-et két szám szorzatára kell bontani, és ahogy már írtam korábban, az sokjegyű számokra nehéz. Itt is a felbontás a lényeg, hiszen odáig az átalakítások teljesen triviálisak:
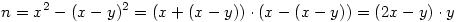
És ha most n páratlan (amit fel lehet tenni, mert ha páros, akkor osztjuk 2-vel, és n/2-et próbáljuk felbontani), akkor annak minden kéttényezős felbontására egyértelműen fogunk kapni egy páratlan y-t és egy egész x-et (n-nek minden y osztójához x=(y+n/y)/2).
Egyébként ennek könnyű megadni egy triviális megoldását, ha n páratlan (helyettesítsd be): x=(n+1)/2, y=1
Amúgy honnan szeded ezeket a felbontásokat?
|
| Előzmény: [445] csewe, 2008-04-11 10:03:14 |
|
| [445] csewe | 2008-04-11 10:03:14 |
 sziasztok
ismét kérnék egy levezetést
n = x négyzet - (x - y) a négyzeten
1 < y < n-1 valószínűleg páratlan
0 <= x pozitív egész
x -et és y -ont keresem
köszi
|
|
| [444] Róbert Gida | 2008-04-10 22:55:10 |
 Érdekes kérdés. Jelölje f(n) az osztók maximális számát (k n!-ig minden egész előáll n!-nak legfeljebb f(n) darab különböző (pozitív) osztójának összegeként). Dinamikus programozással kiszámítható ez a sorozat kis n-ekre: n!-ig minden egész előáll n!-nak legfeljebb f(n) darab különböző (pozitív) osztójának összegeként). Dinamikus programozással kiszámítható ez a sorozat kis n-ekre:
f(1)=1,f(2)=1,f(3)=2,f(4)=3,f(5)=4,f(6)=5,f(7)=5,f(8)=6,f(9)=7,f(10)=7,f(11)=7
Nagyobb n-re már nincs elég memóriája a gépemnek. Egyszerű program O(n!) memóriát igényel.
Hasonlóan az eredeti feladat bizonyításához így minden n 11-re f(n) 11-re f(n) n-4 is teljesül! Sőt szerintem nehéz számelméleti sejtésekkel rögzített c>0-ra f(n)<c*n is teljesül, ha n elég nagy. n-4 is teljesül! Sőt szerintem nehéz számelméleti sejtésekkel rögzített c>0-ra f(n)<c*n is teljesül, ha n elég nagy.
|
| Előzmény: [442] S.Ákos, 2008-04-09 21:37:21 |
|
|
| [442] S.Ákos | 2008-04-09 21:37:21 |
 Sziasztok!
A B.4055-ös feladatnál (Bizonyítsuk be, hogy minden n!-nál nem nagyobb pozitív egész szám felírható az n! legfeljebb n darab különböző osztójának összegeként.) egész könnyen adódik, hogy n-1 tag is elég n>1 esetén. a kérdés az lenne, hogy ennyi mindig kell-e, vagy ez is csökkenthető tovább, ha n nő, és ha igen, melyik az a függvény, ami megadja a tagok minimális számát?
|
|
| [441] Gyöngyő | 2008-04-09 18:16:40 |
 Sziasztok!
Lenne egy olyan kérdésem,hogy milyen esetben lehet parciális integrálást alkalmazni impropius integrál kiszámitására?
Köszike:
Zsolt
|
|
|
| [438] epsilon | 2008-04-09 15:48:31 |
 Köszi nadorp, mindjárt nem is merek szólni, mert ez valóban átvert, és nem is modhatni kemény diónak, én az x=a×cos2t változócsrét alkalmaztam, és tangenshatványnak az integrálja lett, amit csak rekurziósan bonyolítottam :-(
|
|
|
| [436] epsilon | 2008-04-09 14:25:40 |
 A 434. hsz-ban mindenütt (0,1) helyett [0,1] a helyes. Bocs az elírásért!
|
|
| [435] epsilon | 2008-04-09 14:08:01 |
 Annak örömére, hogy nadorp ilyen szép elemi megoldást adott, fe merészkedek tenni még egy feladatot, szimpatikus, de nem ugrik be :-( Igazolandó, hogy:
|
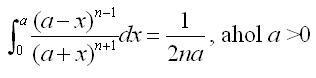 |
|







 n!-ig minden egész előáll n!-nak legfeljebb f(n) darab különböző (pozitív) osztójának összegeként). Dinamikus programozással kiszámítható ez a sorozat kis n-ekre:
n!-ig minden egész előáll n!-nak legfeljebb f(n) darab különböző (pozitív) osztójának összegeként). Dinamikus programozással kiszámítható ez a sorozat kis n-ekre:  11-re f(n)
11-re f(n)