|
| [56] Lóczi Lajos | 2006-01-17 22:15:11 |
 A függvény egyben reláció (=rendezett párok részhalmaza) is.
Akármelyik relációnak van inverze (u.i. a rendezett párok minden egyes tagjában "megfordítjuk" az elemek sorrendjét).
Neminvertálható függvény inverze tehát relációként (mindenféle leszűkítés nélkül) minden további nélkül értelmezhető, csak eme "fordított" reláció nem lesz függvény (azaz nem teljesíti azt a követelményt, hogy közös kezdőtaggal rendelkező rendezett párok második tagja is közös legyen).
Másik megközelítés: az inverz is függvényként fogható fel, ha értékkészletét megváltoztatjuk: halmazértékű függvényekről is lehet, sőt hasznos beszélni. (Régies szóhasználattal ezek a "többértékű" függvények.)
|
| Előzmény: [53] bullat, 2006-01-17 21:46:54 |
|
| [55] bullat | 2006-01-17 22:11:46 |
 Köszönöm lorantfy!
Egyelőre a legnagyobb problémám az, hogy a pontos meghatározását nem tudom. ha ezt valaki meg tudná mondani, akkor lehet hogy egy fél lábbal sikerült a megoldáshoz közelebb jutnom. egyébként nagy vita van, hogy a függvény az csak egyértelmű hozzárendelés lehet mert egy x értékhez csak egy y érték tartozthat. Amúgy mégegyszer köszönöm. Bullat
|
| Előzmény: [54] lorantfy, 2006-01-17 22:01:34 |
|
| [54] lorantfy | 2006-01-17 22:01:34 |
 Szia Bullat!
A fgv. értelmezési tartományát le kell szűkíteni egy olyan halmazra, melyen már kölcsönösen egyértelmű a leképezés.
A legegyszerűbb példa az f(x)=x2 fgv. Ahhoz, hogy az inverze értelmezhető legyen le kell szűkíteni az értelmezési tartományt a nemnegatív számok halmazára.
Vagy a trigonometrikus fgv-ek inverzénél olyan félperioduson értelmezed, ahol már egy-egy értelmű és akkor értelmezhető az inverze.
Alapfokon ennyit tudok mondani, aztán majd mások kiegészítik.
|
| Előzmény: [53] bullat, 2006-01-17 21:46:54 |
|
| [53] bullat | 2006-01-17 21:46:54 |
 Sziasztok!
Szeretném, ha segítemétek, mert egy olyan problémába ütköztem, amit nem tudok egyedül megoldani. A kérdés egyszerű: Hogyan képezhetjük egy kölcsönösen NEM egyértelmű leképzést létesítő függvény inverzét? És ha tudtok légyszi egy példát is!
Előre is köszi. bullat
|
|
| [52] lorantfy | 2006-01-17 20:56:15 |
 Szia Ádámka!
Úgy néz ki, hogy ebben a feladatban nem kell számolni a súrlódással, ugyanis a súrlódásos változat éppen a következő feladat lesz.
Ugye tudod, hogy a 30-60 fokos derékszögű háromszög éppen egy szabályos háromszög fele, így a rövidebbik befogó éppen az átfogó fele.
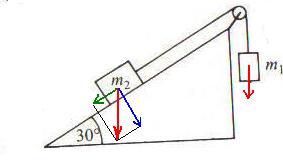
Az m2 testre ható súlyerőt fel kell bontanod egy lejtővel párhuzamos és egy arra merőleges komponensre.
Itt az eredeti háromszöghöz hasonló háromszögek keletkeznek. Így a lejtővel párhuzamos komponens éppen a fele az m2 tömegű test súlyának, (ami 200 N, ha a g értékét közelítőleg 10-nek vesszük), tehát 100 N.
Egyensúly esetén ennyinek kell lenni az m1 tömegű test súlyának, mert a csiga csak az erő irányát változtatja meg. Ebből következik, hogy m1=10 kg.
Ha van súrlódás, akkor megadják a tapadási súrlúdási együttható értékét és ekkor a lejtőre merőleges kompones nagyságát ezzel beszorozva megkapod a súrlódási erő max. értékét. Az előzőleg kapott 100N-hoz hozzáadva és levonva kapod a súlyerő két határértékét melyek között változhat az m1 tömegű test súlya egyensúly esetén.
|
 |
| Előzmény: [51] Ádámka19_91, 2006-01-17 19:22:41 |
|
| [51] Ádámka19_91 | 2006-01-17 19:22:41 |
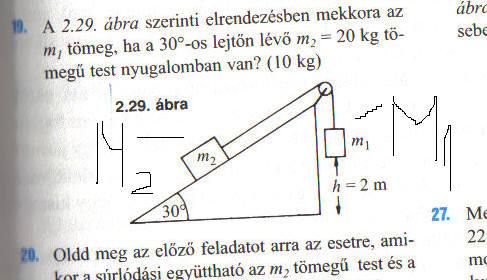
 Sziasztok elnézést hogy itt kérek segítséget de itt volt az utolsó mail. Tehát ha valaki tud segíteni a kkor már 1-2 képlet is nagy segítség hogy legalább megértsem. Tehát a feladatom a következő: (van egy ábra is de azt is leírom hogy milyen infókat árul el) "A 2.29. ábra szerinti elrendezésben mekkora az m1 tömeg, ha a 30 fokos lejtőn lévő m2=20 kg tömegű test nyugalomban van?" Az ábrán egy 30 fokos lejtő van. (tehát egy derékszögű háromszög van rajta és balra a 90 foktól van a 30 fokos és 90 fölött a 60 fokos szög) A derékszöggel szemben lévő oldalon van az m2 test. a 60 fokos szögön egy csiga van és azon egy kötél fut. egyik végen a kötélnek az m2 test van a másik végen a derék szög mellett 2 m magasságban lóg az m1 test. (ja most scanneltem be az ábrát ott lesz sztem valahol) előre is köszönöm tényleg 1-2 képlet is nagy segítség lenne. köszönöm ha már nem bírtam várni akkor adam987@freemail.hu
|
 |
|
| [50] Ádámka19_91 | 2006-01-17 18:56:22 |
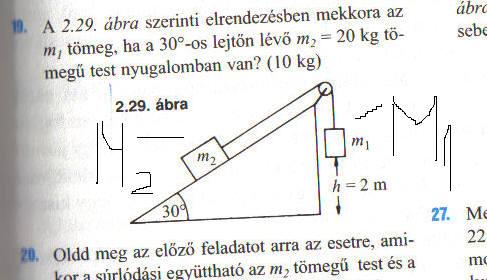
 Sziasztok elnézést hogy itt kérek segítséget de itt volt az utolsó mail. Tehát ha valaki tud segíteni a kkor már 1-2 képlet is nagy segítség hogy legalább megértsem. Tehát a feladatom a következő: (van egy ábra is de azt is leírom hogy milyen infókat árul el) "A 2.29. ábra szerinti elrendezésben mekkora az m1 tömeg, ha a 30 fokos lejtőn lévő m2=20 kg tömegű test nyugalomban van?" Az ábrán egy 30 fokos lejtő van. (tehát egy derékszögű háromszög van rajta és balra a 90 foktól van a 30 fokos és 90 fölött a 60 fokos szög) A derékszöggel szemben lévő oldalon van az m2 test. a 60 fokos szögön egy csiga van és azon egy kötél fut. egyik végen a kötélnek az m2 test van a másik végen a derék szög mellett 2 m magasságban lóg az m1 test. (ja most scanneltem be az ábrát ott lesz sztem valahol) előre is köszönöm tényleg 1-2 képlet is nagy segítség lenne. köszönöm ha már nem bírtam várni akkor adam987@freemail.hu
|
 |
|
|
| [48] Raymond | 2006-01-10 21:22:59 |
 Ebben is tusdz segíteni? INT(1/xx-8x+25) Hasonló képpen kell eljárni itt is vagy esetleg másként?
|
|
|
| [46] Raymond | 2006-01-10 20:42:11 |
 Rájöttem a példa titkára, csináltam egy másikat is. Pl.:int(1/(xx+3))
Szerintem ez a megoldás: gyök3/3*(arctgx/gyök3)+C
Szerinted helyes?
|
|
|
|
|
| [42] Raymond | 2006-01-10 19:09:56 |
 "Most egy olyan helyettesítéses integrált kell csinálni, hogy a 9 átkerüljön olyan helyre, ahol már nem okoz gondot."
Ezt egy kicsit részletesebben fejsd ki nekem légyszíves.
Ez az a rész amit nem értek.
|
| Előzmény: [41] jonas, 2006-01-10 18:41:31 |
|
| [41] jonas | 2006-01-10 18:41:31 |
 Most egy olyan helyettesítéses integrált kell csinálni, hogy a 9 átkerüljön olyan helyre, ahol már nem okoz gondot. Egy egyszerű t=c.x lineáris helyettesítés jó lesz.
|
| Előzmény: [40] Raymond, 2006-01-10 18:22:37 |
|
| [40] Raymond | 2006-01-10 18:22:37 |
 Szia Mihály,
Az alapintegrálok között az arctgx+C-re hasonlít.Én is ezzel próbálkoztam de nem tudok mit kezdeni a 9-el. Azzal mit kell csinálni?Azt is integrálni kell?
Kösz
|
| Előzmény: [39] Fálesz Mihály, 2006-01-10 17:55:03 |
|
| [39] Fálesz Mihály | 2006-01-10 17:55:03 |
 Szia Raymond,
Szerintem úgy tanulsz többet, ha kevesebb segítséget kapsz, és többre jössz rá magad. Az első segítség tehát:
Első lépésként nézd végig az alapintegrálokat, és keresd meg, hogy melyik hasonlít legjobban az  -re. -re.
|
| Előzmény: [38] Raymond, 2006-01-10 15:37:24 |
|
| [38] Raymond | 2006-01-10 15:37:24 |
 Sziasztok,
Most éppen az integrálással foglalkozom és nem igazán akarnak sikerülni a példák. Pl.: int(1/(xx+9))
xx=x a négyzeten
Valahogy nem jövök rá. Szívesen venném ha valaki lépésről-lépésre leírná nekem, hogy mit kell csinálni. Elöre is kösz.
|
|
| [37] !X! | 2006-01-09 18:08:41 |
 Hello Geg!!
Köszönöm a válaszod, sokat segített.
|
|
| [36] Geg | 2006-01-09 14:45:59 |
 A henger egyes retegeiben lokalis termodinamikai egyensuly van, ezert egy-egy ilyen vekony savban ervenyes az allapotegyenlet. Fel kell irni a Newton egyenletet egy ilyen kis retegre: felette es alatta levo gaz nyomasabol szarmazo ero + a sajat sulya. Ebben megjelenik a lokalisan jelen levo suruseg, amit az allapotegyenlettel at lehet jatszani nyomasra, igy kapunk egy differencialegyenletet, de abban szerepel meg a homerseklet is, mint a magassag fuggvenye. Ezt a hovezetes egyenletebol lehet meghatarozni. Mivel az allapot stacionarius, ezert a hovezetes egyenlete miatt a homerseklet magassag szerinti masodik derivaltja nulla (itt feltettuk, hogy a hovezetesi tenyezo nem fugg a helytol), vagyis a fv linearis, es tudnia kell, hogy fent 380K, alul pedig 200K a homerseklet. A nyomasra vonatkozo differencialegyenlet most mar megoldhato, amit az allapotegyenlettel vissza lehet jatszani surusegre. Ha a suruseg ismert a magassag fuggvenyeben, akkor a tomegkozeppont egyszeru integralassal adodik.
|
| Előzmény: [35] !X!, 2006-01-09 10:08:45 |
|
| [35] !X! | 2006-01-09 10:08:45 |
 Sziasztok!!!
Nagyon hálás lennék, ha valaki segítene megoldani ezt a feladatot:
Egy h magasságú, A alapterületű hengeralakú edényben levegő van. Az edény alját 200 K hőmérsékleten, a tetejét pedig 380 K-en tartjuk. Határozzuk meg a tömegközéppont helyzetét!
|
|
| [34] Nandi001 | 2005-12-30 19:00:31 |
 szia lorantfy!
köszi a gyors választ!!!sokat segítettél. igy már nagyon egyszerű, csak nem értettem a jelöléseket.
|
|
| [33] lorantfy | 2005-12-30 18:01:18 |
 Szia Nandi!
f(x,y)=3x2y+2xy2 Ez egy kétváltozós fgv., x és y a két változó. Lehet x szerint és y szerint deriválni és a kapott derivált fgv-eket lehet újra deriválni x és y szerint. Ezek a fgv elsőrendű és másodrendű parciális deriváltjai. Sokféle jelölés van forgalomban.
[fx(x,y)]' az x szerinti első derivált. Ezt úgy kapod, hogy x szerint deriválod a fgv-t miközben a y-t konstansnak tekinted. Az első tagban x2 deriváltja 2x és ezt szorzod 3y-nal. A másodikban 2x-nek pedig 2, szorozva y2-tel így:
[fx(x,y)]'=6xy+2y2
Hasonlóan ha y szerinti deriválsz, akkor az x-et tekinted konstansnak. Igy az y szerinti első derivált: az első tagban 3y-nak 3 és marad az x2 szorzó, a második tagban y2-nek 2y a deriváltja, szorozva 2x-el.
[fy(x,y)]'=3x2+4xy
[fxy(x,y)]'' : ez a másodrendű vegyes parciális derivált. Ezt úgy kapod, hogy az x-szerinti első deriváltat most y szerint deriválod úgy, hogy közben az x-et konstansnak tekinted.
[fxy(x,y)]''=6x+4y
[fyx(x,y)]'' : ez is a másodrendű vegyes parciális derivált, csak a sorrend más. Ezt úgy kapod, hogy az y-szerinti első deriváltat x szerint deriválod úgy, hogy közben az y-t konstansnak tekinted.
[fyx(x,y)]''=6x+4y
Itt ugyanazt kell kapni mint az előbb, szóval nem függ a sorrendtől.
Aztán szokták még kérdezni a az x szerinti második és az y szerinti második deriváltakat.
[fxx(x,y)]'' és [fyy(x,y)]''
Ezeket értelem szerűen úgy kapod, hogy az x szerinti első deriváltat újra x szerint deriválod, illetve az y szerinti elsőt újra y szerint.
[fxx(x,y)]''=6y és [fyy(x,y)]''=4x
|
| Előzmény: [32] Nandi001, 2005-12-30 13:40:23 |
|










