|
| [1063] jenei.attila | 2010-02-13 11:48:03 |
 Az összes lehetséges rendszám 253*103. A páronként különböző betűket tartalmazó betűhármasok száma: 25*24*23, amiből a legalább két egyforma betűt tartalmazó betűhármasok száma : 253-25*24*23. Hasonlóan a legalább két egyforma számjegyet tartalmazó számhármasok száma: 103-10*9*8. A két kifejezés szorzata megadja a betűkben, és a számokban is legalább két egyforma jegyet tartalmazó rendszámok számát. Vagyis a keresett val.-ég:
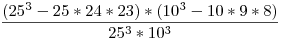
|
| Előzmény: [1054] Fernando, 2010-02-09 10:58:46 |
|
| [1064] Fernando | 2010-02-13 13:16:19 |
 Összes eset ok, ismétléses variációk számának szorzata. Az én gonolatmenetem: kedvezők: tekintsük a betűket: a pár helyét 3-féleképpen tudjuk kiválasztani, a párok száma 25*24 és ehhez hozzáadjuk azokat az eseteket, amikor mindhárom betű azonos -tehát25-öt- hiszen nekünk az is jó. A számoknál ugyanígy járunk el. És kapcsolat van, szorzunk. Kapjuk:
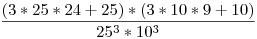
Ez amúgy egyenlő azzal amit te írtál és mzperx-nek is ez jött ki számszerint, a keresett valszín:
0,032704
|
| Előzmény: [1063] jenei.attila, 2010-02-13 11:48:03 |
|
|
|
|
| [1068] torcsi2010 | 2010-02-15 19:53:05 |
 köszi a segítséget és sajnálom hogy a második kép nem jött össze :(
|
|
| [1069] m.atekoos | 2010-02-27 11:24:09 |
 Tudnátok segíteni?
Itt a feladat: egy egységnyi sugarú kör kerületére felvesszük ilyen sorrendben: A C D E B úgy hogy AB átmérő, tehát C,D,E egy félköríven helyezkedik el. Tudjuk hogy AC=DE. Biz be hogy CB+DB+EB>=2.
|
|
|
| [1072] D. Tamás | 2010-03-06 20:29:04 |
 A B.4251-es feladat megoldása közben felmerült bennem egy kérdés: mit értünk egy adott p alapú számrendszer utolsó két számjegyén? Namost, ha p kisebb, mint 11, akkor egyértelmű, de a p nagyobb mint 10 akkor például a 100 a 17-es számrendszerben 515, hiszen 5*17+15*1=100. Éppen emiatt merültek fel nekem gondok, hogy most a 15 az utolsó két számjegy, vagy az 515?
|
|
| [1073] AzO | 2010-03-06 21:13:07 |
 A feladatot ugyan nem ismerem, de pont az indokolja, hogy 515 az utolso ket szamjegy, amit magad is irtal: 5.17+15.1=100, azaz az utolso helyiertekre a 15 kerul, az utolso elottire az 5. Jelolhetnenk betukkel is a 17-es szamrendszer szamjegyeit, es akkor minden egyes helyiertekre egykarakteres szimbolum kerulhetne, mint ahogy az a 10-es szamrendszerben megszokott.
|
| Előzmény: [1072] D. Tamás, 2010-03-06 20:29:04 |
|
| [1074] BohnerGéza | 2010-03-07 17:10:43 |
 Célszerű jelölni a számjegyet, ha nem írható le mind egy karakterrel: pl. (5)(15), vagy (5)(1)(5) mást jelent. Ezt oldják meg a 16-os szr-ben az A=10, B=11, ..., F=15 jelöléssel.
|
| Előzmény: [1072] D. Tamás, 2010-03-06 20:29:04 |
|
| [1075] Janosov Milán | 2010-03-08 15:27:14 |
 Üdv!
A kérdésem valaki olyanhoz szól, aki jártas a Mathematica (7.0.1) kezelésében. Többváltozós függvényt szeretnék integrálni (több változó szerint), de sajnos nem sikerül (a 0-tól 1-ig vett határozott integrálban is lesz változó). Az alábbi szintaxis szerint próbáltam: Integrate[f(x1,x2,x3,...),(x1,0,1),(x2,0,1),...(xn,0,1)] - sima zárójelek helyett persze kapcsossal. Ha valaki tudna adni egy jó példát, hálás lennék!
|
|
| [1076] Alma | 2010-03-08 15:44:53 |
 próbáld a következőt ki:
![f\left[x\_,y\_\right]:=x^2+y^2;](keplet.cgi?k=5495DBE406CD6BD3)
Integrate[f[x,y],{x,0,1},{y,0,1}]
Elvileg ennek így működnie kell, az eredmény 2/3. Próbáld először ezt, majd saját problémádon a szintaxist.
|
| Előzmény: [1075] Janosov Milán, 2010-03-08 15:27:14 |
|
|
| [1078] Alma | 2010-03-08 18:34:29 |
 Igen. Nekem az az általános tapasztalatom, hogy az Integrate parancs sokkal lassabb, ha határozott integrált számoltatsz ki, mintha primitív függvényét kérnéd csak. Így, én vagy határozatlanul integráltatok, vagy az NIntegrate paranccsal numerikusan számoltatok.
|
| Előzmény: [1077] Janosov Milán, 2010-03-08 17:24:05 |
|
| [1079] dfkuu | 2010-03-08 21:07:08 |
 Sziasztok! Sürgős lenne! A De Morgan azonosságot kellen bizonyítanom, de nem Venn-diagram segítségével, sajnos azt nem fogadták el.
Valaki mondja meg!
|
|
|
| [1081] Janosov Milán | 2010-03-09 12:49:09 |
 Köszönöm a javaslatokat, az integrálás mint olyan azt hiszem már nem probléma. A függvényeimet kell egyszerűsíteni (kisebb függvényekre szépen dolgozik), az eredmént - már ha ad egyáltalán - nem szép, és nem is használható :).
|
| Előzmény: [1080] Lóczi Lajos, 2010-03-09 11:55:49 |
|
|
| [1083] Janosov Milán | 2010-03-11 00:33:50 |
 Köszönöm a segítséget, és/de közben sikerült megoldanom a problémát (numerikus integrálással).
És esetleg azt lehet tudni, miért lassult be ma este a munkafüzet olyannyira, hogy esetenként tízszer kellett frissíteni, mire történt valami? Határidőkor ez kicsit tragikus :(
|
| Előzmény: [1082] Alma, 2010-03-09 20:52:53 |
|
| [1084] Marika | 2010-03-12 19:48:09 |
 Sziasztok! Szeretnék segítséget kérni! Megmagyarázná valaki hogy kell ezt a feladatot meg csinálni? Hegyes szögű-e az a háromszög melyben a szokásos jelölésekkel? A=17cm B=11cm C=22cm Előre is köszönöm a segítséget!
|
|
| [1085] Marika | 2010-03-12 20:04:59 |
 Sziasztok! Ebben is segítségre szorulok. Egy háromszög két oldala 6,5cm és 7,3cm a közbezárt szög 72fok. Egy másik háromszög egyik oldala 13,4 a rajta fekvő 2 szög 30fok és 78fok. Egybevágó-e a két háromszög? köszönöm ha segittek megoldani .!
|
|
| [1086] Radián | 2010-03-12 21:26:04 |
 1084-re: Legyenek egy háromszög oldalai a,b,c, ahol a<=b<=c, ekkor a hegyesszögű háromszög oldalaira az alábbi feltétel teljesül: a*a+b*b>c*c ,ha a háromszög derékszögű: a*a+b*b=c*c (Pitagorasz-tétel),ha a háromszög tompaszögű: a*a+b*b<c*c (Ezek gyakorlatilag a koszinusztételből következnek.)
1085-re: Lehet egybevágó is, ha mindkét háromszög oldalainak hossza 6,5;7,3 és 13,4 cm , a szögek pedig a megfelelő módon 72,30,78 fokosak(13,4 cm-es oldalon fekvő 2 szög 30fok és 78fok, a vele szemközti pedig 72)hisz 72+30+78=180. Másképp nem lesz a két háromszög egybevágó.
|
| Előzmény: [1085] Marika, 2010-03-12 20:04:59 |
|
| [1087] HoA | 2010-03-12 21:32:32 |
 A szögek alapján még nem lenne kizárt ( 30 + 78 + 72 = 180 ) , de az egybevágósághoz az kéne, hogy az oldalhosszak is megegyezzenek. Az pedig "ránézésre" is látszik, hogy 72 fokos szöget közbezáró 6,5 és 7,3 cm-es oldalak mellett a harmadik oldal nem lehet 13,4 cm ( alig kisebb, mint a két másik összege, 13,8 ) . Pontos válasz a cosinus tétel alapján: teljesül-e, hogy 13,42=6,52+7,32-2*6,5*7,3*cos72o . Szerintem nem, de számold ki.
|
| Előzmény: [1085] Marika, 2010-03-12 20:04:59 |
|
|
| [1089] Marika | 2010-03-13 16:01:18 |
 Nagyon szépen köszönöm a gyors segítséget!
|
|
| [1090] Fernando | 2010-03-14 23:46:43 |
 A wolfram-ba beírva: zeta(1) ok; zeta(2) ok; zeta(-1)=-1/12. Miért is?
|
|
|
| [1092] farkasroka | 2010-03-15 18:49:37 |
 Sziasztok!
A következő sorozathoz keresnék képletet, ill. még arra lennék kíváncsi, hogy hogyan lehet egy általános lánctörtet átírni egyszerűre?
Segítségeteket előre is köszönöm!
|
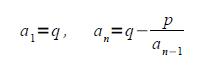 |
|
| [1093] Sirpi | 2010-03-16 11:07:03 |
 Ugye a lánctört határértékben adja ki az értékét, és ha periodikus, akkor az általános trükk az, hogy ezt a határértéket elnevezzük A-nak, és megpróbálunk A-ra felírni egy egyenletet. Mivel 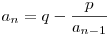 , ezért határértékben: , ezért határértékben:  , vagyis A2-Aq+p=0, és ezt már csak meg kell oldani A-ra, ami egy sima másodfokú egyenlet. , vagyis A2-Aq+p=0, és ezt már csak meg kell oldani A-ra, ami egy sima másodfokú egyenlet.
Persze az még kérdés, hogy a 2 gyök közül melyikhez fog tartani a lánctört...
|
| Előzmény: [1092] farkasroka, 2010-03-15 18:49:37 |
|
|
|
| [1097] bily71 | 2010-03-27 21:34:26 |
 Üdv! Lenne egy kérdésem.
A törtek egészrészével fáradtságos munka a számolás, de azért vannak szabályok, amelyek megkönnyíthetik a dolgunkat, mint pl.: ![[x]-\left[\frac{x}{p}\right]=\left[\frac{(x-1)(p-1)}{p}\right]](keplet.cgi?k=CA0F15F193BE85D0) , vagy pl.: , vagy pl.: ![p\left[\frac{x}{p}\right]=[x-b]](keplet.cgi?k=B87A2531CDD0FC10) , ha a , ha a x<a+1, ahol a x<a+1, ahol a b (mod p), stb., (x b (mod p), stb., (x R, a,b R, a,b N, p N, p P). P).
Nem találtam megfelelő irodalmat, hol lehet bővebben olvasni erről a témáról?
|
|
|
| [1099] Hölder | 2010-03-28 13:18:20 |
 Sziasztok! Arra lennék kiváncsi, hogy van -e olyan függvény, ami bármely valós szám esetén értelmezve van és a racionális pontokban folytonos, az irracionális pontokban pedig nem az?(pont a Riemann -féle függvénynek az "ellentettje")
|
|
|
| [1101] Maga Péter | 2010-03-29 08:52:14 |
 A bizonyítás ,,helyből'' valóban nem könnyű. Van azonban egy valós függvénytani elmélet, aminek ez az egyik első alkalmazása. Lényegében azt lehet bebizonyítani, hogy egy valós-valós függvény folytonossági pontjainak halmaza előáll megszámlálható sok nyílt halmaz metszeteként (ez egyszerű következménye a folytonosság definíciójának); a racionális számok halmaza pedig nem (ez pedig következik Baire kategóriatételéből).
|
| Előzmény: [1100] jonas, 2010-03-28 13:30:57 |
|
| [1102] K Robi | 2010-04-03 19:41:56 |
 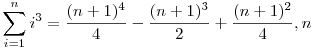 természetes szám. természetes szám.
Meg tudná valaki mutatni a bizonyítását? Természetesen egy link is tökéletesen megfelelő olyan helyre, ahol megtalálom (lehetőleg magyar vagy angol vagy német nyelven).
|
|
|
|
|
|
| [1107] HoA | 2010-04-07 08:53:11 |
 A Geometria [1404] –ben kitűzött feladat szerepel Reiman István „Geometria és határterületei” és „Fejezetek az elemi geometriából” könyveiben. A megoldás ötlete az, hogy a komplex síkon az n-ik egységgyököket feleltessük meg a szabályos n-szög csúcsainak. Ezek az ei egységgyökök a zn=1 egyenlet megoldásai, a P=zn-1=0 polinom nullhelyei, ahol e0=1. Ezért a polinom felírható P=(z–1)(z–e1)...(z–en-1) alakban. Ugyanakkor zn-1=(z–1)(zn-1+zn-2+...+z+1) Mindkét kifejezést z-1 tényezővel osztva az adódó kifejezések z=1 helyen vett abszolútértékére adódik, hogy |(1–e1)|.|(1–e2)|...|(1–en-1)|=1+1+..+1=n és itt a baloldal éppen a z=1 csúcsból a többi csúcsba húzott átlók hosszának szorzata.
A kérdés: „Középiskolában tanultuk”, hogy egy ilyen z-1 -gyel történő egyszerűsítés után a továbbiakban ki kell kötnünk, hogy z 1 . Itt pedig a folytatásban éppen a z=1 helyen nézzük a dolgokat. Nem hiányzik itt valami? 1 . Itt pedig a folytatásban éppen a z=1 helyen nézzük a dolgokat. Nem hiányzik itt valami?
|
|
|
| [1109] Marika | 2010-04-11 15:44:20 |
 Sziasztok ! Valaki segítene megoldani?
Egy háromszög oldalfelező pontjai (-2;-2),(5;1),(3;4) a, Számítsuk ki a háromszög csúcsainak koordinátáit. b,Számítsuk ki az eredeti és a z oldalfelező pontok által meghatározott háromszögek súlypontjainak koordinátáit. Mit tapasztalunk?
És még egy lenne
Az ABC háromszög A csúcsának helyvektora a/vektor/(-2;3),AB/vektor/=7i-2jés CB/vektor/=3i-6j Számítsuk ki a háromszög csúcsainak és súlypontjának koordinátáit.
Lécci segítsetek megoldani de ha lehet magyarázattal, hogy utána egyedül is sikerüljön. Előre is köszönöm a segítséget!!!!!!!!!
|
|
| [1110] Maga Péter | 2010-04-11 16:01:03 |
 Vagy mondhatjuk azt, hogy nem a zn-1=(z-e0).....(z-en-1), hanem a zn-1+...+z+1=(z-e1).....(z-en-1) azonosságba helyettesítünk z=1-et. Ezzel nem használunk folytonosságot.
|
| Előzmény: [1108] nadorp, 2010-04-07 11:08:02 |
|
| [1111] z1z9z9z2 | 2010-04-11 17:52:10 |
 Szia! Az első feladatban oldalfelező pontok vannak megadva, ha ezeket összekötöd, akkor a háromszög középvonalait kapod. A középvonal párhuzamos az oldallal és fele akkora. A háromszög oldalfelező pontjai: Oa;Ob;Oc c/vektor=Oa/vektor+OcOb/vektor, és így tovább Majd a háromszög súlypontja S=(a+b+c)/3 A másodikban meg egy kis pontosítást kérek:) Te csak egy koordinátát jelölsz a másodiknál ugye?Az i, és j az egységvektorok?
|
| Előzmény: [1109] Marika, 2010-04-11 15:44:20 |
|
|
|











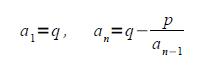

 x2, akkor
x2, akkor 
 x<a+1, ahol a
x<a+1, ahol a b (mod p), stb., (x
b (mod p), stb., (x R, a,b
R, a,b


