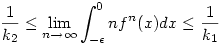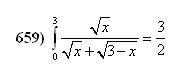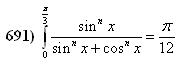| [454] Valvehead | 2008-04-12 23:43:06 |
 Na ja, ennyit sem tudok begépelni.. Három válaszlehetőség is van:
a) 2 b) 5 c)7
Jó, attól hogy egy ismeretlen fokszámú polinomnak megadunk véges számú pontját nem lesz határozott. Igazad van, arra gondoltam, hogy legalább 3-adfkú. Én nem tudom megoldani a feladatot, ezért kérek segítséget.
|
| Előzmény: [453] Róbert Gida, 2008-04-12 15:31:00 |
|
| [455] Káli gúla | 2008-04-12 23:45:04 |
 Hasonló, talán még elvetemültebb a 6,2,5,5,4,5,6,... sorozat, internet nélkül elég reménytelen folytatni. Szintén megtalálható ugyanott: A010371.
|
| Előzmény: [453] Róbert Gida, 2008-04-12 15:31:00 |
|
| [456] Róbert Gida | 2008-04-13 02:37:58 |
 Szerintem nézd meg a belinkelt sorozatot, tizedik eleme éppen 2. Valószínű, hogy erre a sorozatra gondoltak, annyira nem elvetemült (bár szinte lehetetlen kitalálni), a sorszáma is roppant alacsony (2963), ez azt jelenti, hogy ez a Sloane sorozatos könyvében is megjelent.
Katonaságnál az alkalmassági teszt (vagy hogyhívják?) volt ilyen, matematika rész csak ilyen *feladatokból* állt egy oldalon minden sorban a megkezdett sorozatot kellett folytatni. Igazolásom nem lévén 3-szor is volt szerencsém kitölteni ugyanazt a tesztet, azt hiszem a végén már majd 100 százalékra, nyelvtani-fizikai rész már nem ment ilyen jól. Bár gondoltam arra is, hogy szándékosan hülyének tettetem magam és elrontom, simán ment volna. Szerencsére megszüntették a sorkatonaságot mire ténylegesen behívtak volna.....
|
| Előzmény: [454] Valvehead, 2008-04-12 23:43:06 |
|
| [457] Valvehead | 2008-04-13 09:51:33 |
 Lehet, hogy tényleg ez a sor a megoldás. Köszönöm szépen. Ezek szerint nem csak én útáltam a "hülye szabályú" kitalálós sorozatokat? Azért volt érdekes ez a kérdés, mert az összes többi feladat nem ütötte meg a versenyszínvonalat.
|
| Előzmény: [456] Róbert Gida, 2008-04-13 02:37:58 |
|
| [458] hegeduscs | 2008-04-13 11:52:16 |
 Van egy 5-es feladatom: Van egy számsorozatunk: 11,13,15,19,25,35,42 A)Mi a kapcsolat a számok között? B)Folytasd a sort! Üdv, Csabi
|
|
|
|
| [461] Borgi | 2008-04-16 21:31:58 |
 üdv!
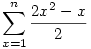
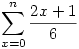
ilyen finomságokkal, mit kezdhet az ember középiskolás szinten?
|
|
| [463] jonas | 2008-04-17 09:04:45 |
 A szummázást lineáris módon szétszedheted.
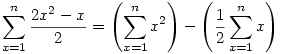
Ezután esetleg megváltoztatod az indexeket, és az egyszerűbb összegeket megtanulod fejből. (Az indexeket a szerint változtatod meg, amilyen változatát az összegeknek megtanultad.)
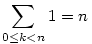
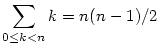
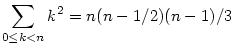
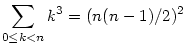
Szerezd meg könyvtárból Graham--Knuth--Patashnik Konkrét Matematikáját. Ennek a könyvnek lehet, hogy vannak nagyon nehéz részei is, amit középiskolás szinten nem értessz meg, de az első része, ami az ilyen összegek kezelésére megtanít, biztosan sokat segít. Nagyon jó könyv.
|
| Előzmény: [461] Borgi, 2008-04-16 21:31:58 |
|
|
|
| [465] epsilon | 2008-04-21 20:09:49 |
 Helló! Megint találtam egy K.O. feladatot: Egy számtani és egy mértani sorozat 4 megfelelő indexü tagjait páronként összeadva, a 18, 18, 26, 58 számokat kapjuk. Mennyi a mértani sorozat állandó hányadosa? Van-e valakinek valami tippje? Előre is köszönöm! Üdv: epsilon
|
|
|
| [467] Doom | 2008-04-21 21:39:29 |
 Ehhez te feltetted, hogy egymást követő elemekről van szó? Vagy a "megfelelő" pont ezt jelentené? Csak mert ez nagyban leegyszerűsítené a feladatot... :)
|
| Előzmény: [466] S.Ákos, 2008-04-21 20:58:08 |
|
| [472] Doom | 2008-04-21 22:22:32 |
 Ugyanis ekkor, ha a két sorozat:
a, a+d, a+2d, a+3d és b, b*q, b*q2, b*q3
akkor felírhatjuk a következő összefüggéseket:
a+d+b*q=a+b+d+b*(q-1)=18-ba behelyettesítve (1)-et:
| d+b(q-1)=0 -> b(q-1)=-d | (2) |
Továbbá a+2d+b*q2=a+b+2d+b(q2-1)=26-ba beírva (1)-et és felbontva a zárójelet:
2d+b(q-1)(q+1)=8
ebbe beírva (2)-t:
| 2d-d(q+1)=d(2-q-1)=d(1-q)=8 | (3) |
Továbbá a+3d+b*q3=a+b+3d+b(q3-1)=58-ba beírva (1)-et és felbontva a zárójelet:
3d+b(q-1)(q2+q+1)=40
ebbe beírva (2)-t:
| 3d-d(q2+q+1)=d(3-q2-q-1)=d(2-q2-q)=40 | (4) |
Most vegyük (3)/(4)-et, ahol d-vel tudunk egyszerűsíteni, ugyanis d nem lehet 0, különben se (3), se (4) nem teljesülne. Ekkor:
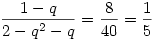
5-5q=2-q2-q
q2-4q+3=0
Megoldva ezt a másodfokú egyenletet q1=3, ekkor d=-4 illetve q1=1, ekkor (3) alapján d*(1-1)=d*0=8 ami ellentmondás.
Tehát (ha az előző hozzászólásomban lévő feltételekkel élünk) az egyedüli megoldás a mértani sorozat hányadosára q=3
|
| Előzmény: [465] epsilon, 2008-04-21 20:09:49 |
|
| [468] Káli gúla | 2008-04-22 00:17:37 |
 Felhasználhatjuk, hogy egy q hányadosú mértani sorozat különbségi sorozata is q hányadosú mértani sorozat. Alkalmazzuk ezt kétszer az összeg sorozatra. Ezt lehet tagonként, ezért a számtani sorozat rész eltűnik, és az összeg második differenciáinak hányadosa az eredeti mértani sorozat hányadosa lesz:
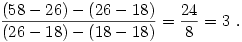
|
| Előzmény: [465] epsilon, 2008-04-21 20:09:49 |
|
|
| [470] epsilon | 2008-04-22 06:44:24 |
 Huh de szép megoldások! Kösz szépen Mindkettőtöknek! Üdv: epsilon
|
|
| [471] epsilon | 2008-04-22 06:46:59 |
 Helló Doom! Az elkezdését Én is így próbáltam, de nem mertem egyértelműen az a+b=18 összefüggést felírni, hiszen negatív rációk esetén, nem biztos, hogy ez az összeg kell adja a legkisebb eredményt, vagy tévedek? Üdv: epsilon
|
| Előzmény: [472] Doom, 2008-04-21 22:22:32 |
|
| [473] Doom | 2008-04-22 07:31:52 |
 Szia! Pont ezért nem szívlelem a "megfelelő" szót, mert mindenki mást érthet alatta. Visszagondolva középiskolás éveimre, mi úgy tanultuk, hogy ez kb az "egymás utáni, sorrendben" kifejezésekkel azonos, bár láthatod hogy először én is bizonytalan voltam ebben. Ha azonban elfogadjuk, akkor az is feltehető hogy a 18, 18, 26, 58 úgy van megadva, hogy az első, második, harmdik, negyedik tagok összege ennyi ("megfelelő" sorrendben :)).
Próbálkoztam a teljesen általános megoldással is (nem egymás utáni tagok pl.), de akkor túl sok az ismeretlen egy egyértelmű megoldáshoz.
Ui: a (4)es egyenletbe sajtóhiba csúszott, az természetesen 40-nel egyenlő és nem pedig 8-cal - Javítottam (Sirpi).
|
| Előzmény: [471] epsilon, 2008-04-22 06:46:59 |
|
| [474] Csimby | 2008-04-22 14:34:09 |
 Ha a "megfelelő" nem egymás utánit jelent, akkor ez a megállapítás semilyen plusz információt nem adna, hiszen pl. bármely 4 természetes szám egy számtani sorozat megfelelő indexű tagja (1,2,3,... - számtani sorozaté).
|
|
| [475] Sirpi | 2008-04-22 14:55:52 |
 Egy probléma (nem tudom a megoldást, sőt azt se, hogy mennyire nehéz, csak eszembe jutott): Ha egy r1, r2 és r3 sugarú kör páronként kívülről érinti egymást (3 kül. pontban), akkor ki lehet a három sugárral fejezni az őket a) kívülről b) belülről érintő kör sugarát? Esetleg szerkeszthetők a középpontok?
|
|
|
|
|
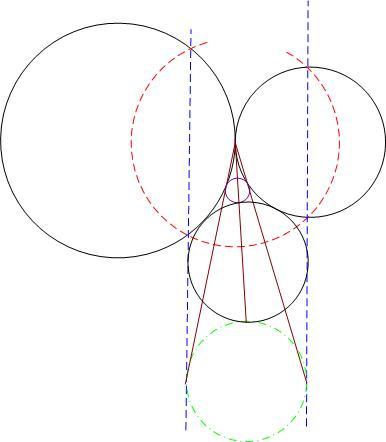
| [479] HoA | 2008-04-22 17:54:24 |
 Én is. De ha már lerajzoltam, felteszem a szerkesztés megoldását. Inverzióval egyszerű. Legyen az inverzió középpontja a két nagyobb - ha van - kör ( k1 és k2 ) érintési pontja, alapköre pedig a harmadik körre ( k3 )merőleges. ( piros kör ). Ekkor k3 inverze önmaga, a másik kettőé két párhuzamos, k3-at érintő egyenes (kék) . A szerkesztendő kör inverze érinti k3-t és a két egyenest (zöld). A szerkesztendő érintési pontokat a zöld kör érintési pontjainak az inverzió középpontjából történő vetítésével kapjuk (barna egyenesek).
|
 |
| Előzmény: [478] jonas, 2008-04-22 16:41:19 |
|
| [480] Sirpi | 2008-04-23 11:20:34 |
 Köszi a válaszokat! Akkor nem is agyalok tovább rajta :-)
|
|
| [481] epsilon | 2008-04-23 14:47:55 |
 Helló Doom és Csimby!A feladat fordításból származik, többször is átnéztem, de SEHOL sem ír arról, hogy EGYMÁSUTÁNI tagok lennének, úgy írja, hogy 4 azonos (egyforma) sorszámú (indexű) tagok páronkénti öszegéről van szó! Sajnos ebben az esetben nem látom be a Káli gúla szép megoldásában, hogy az úgy lenne :-( és olyan kár lenne érte :-(
|
| Előzmény: [473] Doom, 2008-04-22 07:31:52 |
|
|
| [483] epsilon | 2008-04-23 15:54:54 |
 Helló Doom! Úgy fordítottam, és ez alapján úgy értem, hogy mindkét sorozatból összeadjuk pl. az m-edik, n-edik, p-edik, s-edik tagokat, ahol az m, n, p, s nem föltétlen egymás utáni számok.
|
| Előzmény: [482] Doom, 2008-04-23 15:32:13 |
|
| [484] nadorp | 2008-04-24 09:52:46 |
 Ekkor Doom megoldását általánosítva k<m<n pozitív egészekre a
qn-(4k+1)qm+(5m-n)qk+(4k-5m+n)=0
egyenletnek kell keresni az összes q 1 valós megoldását. Kérdés, hogy mindig van-e? 1 valós megoldását. Kérdés, hogy mindig van-e?
Pld. k=1 m=2 n=4 esetén q2+2q-2=0 vagy
k=1 m=3 n=5 esetén q3+2q2-2q-6=0
|
| Előzmény: [483] epsilon, 2008-04-23 15:54:54 |
|
| [485] epsilon | 2008-04-25 14:30:03 |
 Hát akkor ezek szerint, a több mint 1000 feladatot tartalmazó könyvből kb ez a 3. hibás (hiányos megfogalmazásu,) feladat.
|
|
| [486] epsilon | 2008-04-27 10:37:40 |
 Helló!Megint gyűltek keményebb feladatok, a következő integrálok esetén sorra valahol belefulladtam, vagy regény lett a megoldásból :-( ha Valakinek van valami örlete, előre is köszönöm! Üdv: epsilon
|
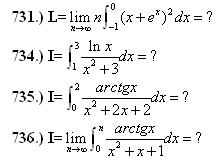 |
|
| [487] epsilon | 2008-04-28 09:50:50 |
 A 734. meglett :-) , szép feladat!
|
|
|
|
| [490] epsilon | 2008-04-28 15:18:50 |
 Elnézést, a 731. feladatban a KÜLSŐ 2 helyett van az n (nem belül, ott e az x hatványon van), amásik esetben úgy van, ahogyan jonas kihangsúlyozta!
|
|
| [491] epsilon | 2008-04-28 16:18:35 |
 A 735. is hosszas ütközetek után kinyírva, az x=(2-t)/(1+2t) változócserével egy kiszámítható, meg az eredeti integrál ellentettje lett. Szóval ez sem volt piskót! Még maradt 2, de közben megint gyűlt vagy 10 :-(
|
|
| [492] epsilon | 2008-04-29 06:44:10 |
 A 731.-hez ha Valaki egy rekurziós öszefüggést tudna megállapítani, az is elég lene...
|
|
| [493] Róbert Gida | 2008-04-29 08:57:50 |
 Az első és az utolsó limesz persze csak úgy értelmes, hogy az integráloknál az integrációs konstans mindig 0, különben a limesz nem létezik, hiszen csak konstans erejéig meghatározott az integrál.
|
| Előzmény: [492] epsilon, 2008-04-29 06:44:10 |
|
| [494] Sirpi | 2008-04-29 10:03:01 |
 Na ezt gondold át még egyszer :-) A függvény primitív függvénye valóban csak konstans erejéig meghatározott (legyen F(x)+c), de mivel rögzített intervallumon integrálunk, ezért az integrál értéke pl. az első esetben F(0)+c-F(-1)-c=F(0)-F(-1) teljesen független a konstans megválasztásától - ami nem is csoda, mert az integrál megegyezik ezen az intervallumon a görbe alatti területtel.
|
| Előzmény: [493] Róbert Gida, 2008-04-29 08:57:50 |
|
| [495] epsilon | 2008-04-29 13:57:56 |
 Ha segítene valamit, a 731.-nek a limesz értéke 1/2, próbáltam még Taylor sorral, az sem jött össze, a Newton Binomiális képlet az nem dobja ki az 1/2-öt, tehát ha azzal próbálom, valami összeg limeszeként kellene előálljon, de még mindig a rekurzióval próbálkozom, akár másodrendű is jó lenne...A 736-ot is a 735 mintájáta analóg változcserével, nem alakult úgy egyenlenek, mint a 735, a nevező megváltozott :-(
|
|
|
|
| [498] epsilon | 2008-04-30 08:24:11 |
 Nagyszerű nadorp! Ez volt az egyetlen transzformáció ami változatlanul hagyta a nevezőt és a számlálóval is volt mit kezdeni. Természetesen a mezei integrál 4/4-el szorozva, azonnal kijön. Köszi szépen, ez sem volt piskóta, még maradt a 731. amire kiváncsi vagyok, megint egyedi-e a megoldása. A felygyült integráltesókat szerencsére ritkítottam, de ezek keményebb diók voltak Üdv: epsilon
|
| Előzmény: [497] nadorp, 2008-04-29 21:06:23 |
|
|
| [500] epsilon | 2008-05-02 08:33:38 |
 Kedves Káli gúla! Köszi, hogy foglalkozol a problémával, és általánosítottabb formában elsőfokú föggvénnyel próbáltad asszimptótikusan megközelíteni az integrandusz alatti függvényt. Megpróbáltam emésztgetni a leírtakat, de amikor az utolsó integrálhoz értem, vagyis amit lennebb beteszek, ahoz, hogy ott a limesz 1/2 legyen szükséges a k1=k2=2...és akkor az azelőtt levő x+e(expx) közrefogása egy egyenlőségé alakúlnak, ami nem igaz. Ha tévedek,vagy rosszul értettem valamit, légyszíves javíts ki, mert a feladat megoldása ami érdekel, nem az, hogy keressem a kákán a csomót...de úgy látom, hogy..ahol jeleztem, elakadtam. Előre is kösz, üdv: epsilon
|
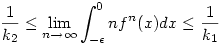 |
| Előzmény: [499] Káli gúla, 2008-05-01 23:13:41 |
|
| [501] epsilon | 2008-05-02 09:07:35 |
 Kedves Káli gúla! Az általánostott ötleted alapján úgy látom, hogy a feladatom esetén elegendő olyan a, b valós számokat találni, amelyekre 2x+a<=f(x)<=2x+b. Ennek érdekében tekintetem egy g(x)=f(x)-2x-k segédfüggvényt a (-1;0) intervallumon. Mivel itt, ennek a deriváltja nem pozitív, ezért itt a g(x) monoton csökkenő, vagyis g(0)<=g(x)<=g(-1) ahonnan a=-k é b=1+1/e -k megfelel (sőt pl. k=1 esetén még egyszerűbbek a korlátok). Ezzl a közrefogássak, az általad leírt lineáris függvény integrálása alapján a limesz láthatóbban 1/2 (persze nem olyan szép általánosan mint Te írtad). És az f'(0) pedig az e(expx) Taylor sorbafejtés (a 0 körül) második tagjára emlékeztet. Most csupán az a "gondom", hogy mivel ez a feladat középisklásoknak feleletválasztós teszt, hogyan lehet ép ésszel meggyőzni egy jobbacska diákot, hogy miért éppen a 2x+k típusú fogófüggvényt kerestem, vagyis miért van ott 2 és miért nem MÁS szám? Én erre csak az e(expx) Taylor sorbafejtésévől látom az f(x)-ben 2 megjelenését...valami más emészthetőbb tipp? Ismételten köszönöm a tartalmas, szinvonalas segítségedet, ami nélkül nem lett volna ez a happy End. Üdv: epsilon
|
|
| [502] epsilon | 2008-05-02 15:11:49 |
 Helló! Szerencsémre már fogytá vannak az integrálok :-) Az alábbi integrállal csupán annyi a bajom, hogy Én az x/(3-x)= t×t változócserét láttam ésszerűnek, azzal kijön az adott eremény. Van valami egyszerűbb megoldás, ahol nem kell ennyit számolni? Előre is kösz, üdv: epsilon
|
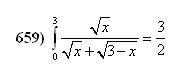 |
|
| [503] epsilon | 2008-05-02 15:29:53 |
 Helló! A feltételezhetően utolsó (?) integrál az alábbi: ezzel az a gond, hogy nagyon hosszas, és az eredmény duplája az-az pi/6 jött ki a pi/12 helyett. A megoldásvázlat: Legyen I ugyanaz az integrál mint a képen, de 0 és pi/2 között. Ezt felbontottam I=I1+I2+I3 integrálokra, pi/6 és pi/3 osztópontoknál. Hozzárendeltem a J=J1+J2+J3 társintegrálokat, amik ugyanolyanok mint az előzőek, de a számlálókban sin helyett cos van. Nem nehéz igazolni, hogy I=J=pi/4. Ezután változócseréket végeztem és I1=J3, és ilyesmik adódtak. Az lett a vége, hogy mind a 6 számozott integrál egyenlő, és közös értékük pi/12. De ezzel, a kitűzött feladat integrálja I1+I2=pi/6 és nem pi/12 :-( A megoldásom hibás, vagy a kitűzött feladatban a felső korlát pi/6 kellene legyen a pi/3 helyett? Vagy ??? Ez a feladat, kösz, üdv: epsilon.
|
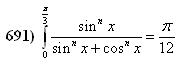 |
|













 1 valós megoldását. Kérdés, hogy mindig van-e?
1 valós megoldását. Kérdés, hogy mindig van-e? 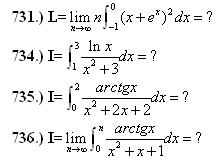

 , ráadásul az integrál se nehéz, hiszen csak az e2x-et, x.ex-et és x2-et kell hozzá integrálni, egyikkel sincs gond.
, ráadásul az integrál se nehéz, hiszen csak az e2x-et, x.ex-et és x2-et kell hozzá integrálni, egyikkel sincs gond.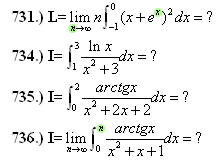
 esetén |f(x)|<h<1, és így a (-1,-
esetén |f(x)|<h<1, és így a (-1,- 0-val lehet felülről becsülni. Lineáris függvényekre könnyen kiszámolhatjuk az integrált -
0-val lehet felülről becsülni. Lineáris függvényekre könnyen kiszámolhatjuk az integrált - f(x)
f(x)