| [759] Kiss Béla | 2009-01-29 20:53:36 |
 Sziasztok! Sagítséget szeretnék kérni a következő feladathoz. Foggalmam sincs, hogy hogyan lehetne megoldani:
Bizonyítsuk be, hogyha a p és q pozitív egész számokra fenn áll a pqp=qpq, akkor p=q.
|
|
| [760] nadorp | 2009-01-30 08:09:03 |
 Ha p=1 akkor q=1 és fordítva, tehát ezekben az esetekben igaz az állítás. Feltehető, hogy p,q 2. Tegyük fel, hogy p<q. Ekkor a feladatban szereplő egyenlőség úgy állhat fenn, ha p kitevője nagyobb, azaz 2. Tegyük fel, hogy p<q. Ekkor a feladatban szereplő egyenlőség úgy állhat fenn, ha p kitevője nagyobb, azaz
qp>pq
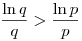
Mivel az 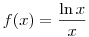 függvény x függvény x e esetén szigorúan monoton csökken, ezért 3 e esetén szigorúan monoton csökken, ezért 3 p<q esetén a fenti egyenlőtlenség nem állhat fenn. Marad a p=2 eset. Ekkor p<q esetén a fenti egyenlőtlenség nem állhat fenn. Marad a p=2 eset. Ekkor
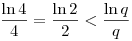 miatt szintén a monoton csökkenésből adódóan q<4,tehát csak q=3 lehet. Viszont a p=2 q=3 értékek esetén nem teljesül az eredeti egyenlőség. Azt kaptuk, p<q nem lehet. Teljesen hasonlóan adódik, hogy p>q sem lehetséges, tehát p=q miatt szintén a monoton csökkenésből adódóan q<4,tehát csak q=3 lehet. Viszont a p=2 q=3 értékek esetén nem teljesül az eredeti egyenlőség. Azt kaptuk, p<q nem lehet. Teljesen hasonlóan adódik, hogy p>q sem lehetséges, tehát p=q
|
| Előzmény: [759] Kiss Béla, 2009-01-29 20:53:36 |
|
| [761] Tibixe | 2009-01-30 16:26:18 |
 Az analízissel szenvedjenek csak a fizikusok, az esetszétbontogatással meg a hentesek... Gyönyörűen kijön számelmélettel.
Vegyük mindkét oldal p alapú logaritmusát.
qp=(logp q) pq
Tehát logpq racionális, t/s alakban felírható, ahol t és s relatív prím egészek.
Innen
sqp=tpq
Ekkor lesz egy u pozitív egész szám, amire
p=ut q=us
Visszahelyettesítve:
t usut=s utus
Az általánosság megszorítása nélkül feltehetjük, hogy
sut ts ts
. Az előző egyenlet mindkét oldalát osztva:
t=s utus-sut
Az előző feltétel miatt utus-sut egész. Mivel t és s pozitív relatív prím egészek, utus-sut csak 1 lehet. Tehát t=s. Az egyetlen önmagával rel. prím pozitív egész pedig az 1. Innen pedig
p=u1=q
|
|
| [762] Tibixe | 2009-01-30 16:36:04 |
 Hoppá,
sut tus tus
helyett
sut tus tus
-et akartam írni.
|
|
| [763] nadorp | 2009-01-30 19:24:28 |
 Köszi az építő megjegyzést, azért nem kell mindjárt leszedni az emberről a keresztvizet egy egyébként jó és nem bonyolult megoldás miatt ( lásd hentes) :-( Egyébként a számelmélet tele van analízist is tartalmazó bizonyítással,ezért nem értek Veled egyet teljesen. Én a pozitív egészeknek azt a tulajdonságát használtam, hogy számtani sorozatot alkotnak, Te meg a számelmélet alaptételét. Mindkettő jó. Ennyi.
|
| Előzmény: [761] Tibixe, 2009-01-30 16:26:18 |
|
| [764] Tibixe | 2009-01-30 20:14:52 |
 Úgy látszik eltér a humorérzékünk.
|
|
|
| [766] Tibixe | 2009-01-30 23:19:16 |
 Amit nekem sikerült, röviden:
Egy d=q-p behelyettesítés, utána a (p+d)p binomiális tételes kibontása, utána az egész szerencsétlenség leosztása pp+d-vel. Amit kapunk, az éppen a
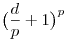
kibontott alakja lesz. Na ennek kéne 1-gyel egyenlőnek lennie. Tehát
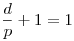
( esetleg -1, de az gyorsan kizárható ), innen pedig
d=0
.
|
|
| [767] Tibixe | 2009-01-31 11:06:04 |
 Közben leesett, hogy amit tegnap írtam, az elég nagy hülyeség... Bocsássatok meg, elég álmos lehettem.
|
|
| [768] Ágoston | 2009-02-02 20:22:25 |
 Adott a síkon egy pont és egy egyenes. Körző használata nélkül szerkesszük meg a pontnak az egyenesre vonatkozó tükörképét. Használhatunk egyenes vonalzót a szokásos módon és egy egységsugarú körlapot, aminek nem ismerjük a középpontját. Ez utóbbit körvonalzóként használhatjuk, vagyis a síkon adott ponton, illetve pontokon átmenő egységsugarú körvonalakat tudunk rajzolni, de a középpontokat nem tudjuk bejelölni.
Valaki tudja a fenti feladatra a megoldást? Köszönöm
|
|
| [769] jenei.attila | 2009-02-02 21:32:36 |
 Ha az adott pont 2 egységnél közelebb van a tengelyhez, akkor könnyű dolgod van. Egyszerűen ráilleszted a körlap szélét a tükrözendő P pontra úgy, hogy a körvonal két pontban metssze a tengelyt. Megjelölöd ezt a két pontot, majd a körlap szélét úgy illeszted ezekre, hogy most az előző helyzethez képest a tengelyre szimmetrikusan helyezkedjen el a körlap, majd körberajzolod a körlapot (a tengelyen kijelölt egymáshoz két egységnél közelebbi pontokra kétféleképpen-tengelyszimmetrikusan-illeszthető a körvonal). Ugyanezt megcsinálod mégegyszer úgy, hogy most az körvonal másik két pontban metssze a tengelyt. A körlap körberajzolásával adódó két körvonal metszéspontja a tengely másik oldalán megadja P tükörképét. Ha 2 egységnél távolabb van P a tengelytől, akkor segéd tengelyeket vehetsz fel úgy, hogy azok az eredeti tengely egy pontján menjenek át. A segédtengelyeket a fent leírt módon tükrözheted az eredeti tengelyre. Így az eredeti tengellyel együtt páratlan sok egy ponton átmenő tengelyed lesz, amelyekre sorban elvégezve a tükrözéseket (először a P-hez legközelebbi tengelyre türözve, majd továbbtükrözve a következő tengelyre, stb.) páratlan sok tükrözés után megkapod P tükörképét.
|
| Előzmény: [768] Ágoston, 2009-02-02 20:22:25 |
|
| [770] Bocsa Dávid | 2009-02-02 21:38:36 |
 Bizonyítsuk be, hogy a Simson-egyenes felezi az MP szakaszt, ahol M a háromszög magasságpontja és P a Simson egyenes P pontja a háromszög körülírt körének körívén. Vki ötlet?
|
|
| [771] HoA | 2009-02-03 12:55:41 |
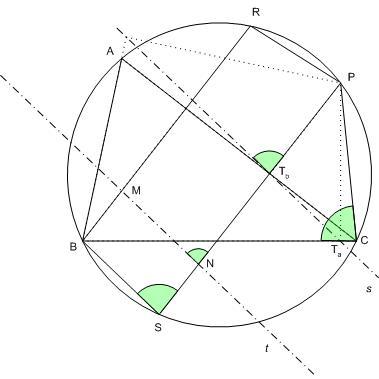
 Legyen az ABC  körülírt körének P pontjából az a oldalra bocsátott merőleges talppontja Ta, a b oldalra bocsátott merőleges talppontja Tb, a körrel alkotott második metszéspontja S. A B-ből induló magasság és a körülírt kör második metszéspontja R. Az s Simson egyenes P-ből vett kéteszeres nagyítása a t egyenes, ennek metszéspontjai BR-rel M, PS-sel N. PCTaTb húrnégyszög, mert Ta és Tb PC Thálesz-körén vannak. PC Ta = PCB szög egyenlő a Tb -nél lévő külső szöggel. PCB és PSB szögek is egyenlők, mint a PB húrhoz tartozó kerületi szögek. Végül s és t egyenesek párhuzamossága miatt PNM szög is az előbbiekkel egyenlő. PRBS szimmetrikus trapéz, mint a körből két párhuzamos húr által kimetszett négyszög. Az N-nél ill. S-nél lévő szögek egyenlősége miatt NPRM is szimmetrikus trapéz. t definíciója miatt PTb=TbN, a PN-re merőleges AC tehát NPRM szimmetriatengelye, így R és M egymás tükörképei AC-re. Mivel a magasságpont oldalegyenesre vett tükörképe a körülírt körön van, M az ABC körülírt körének P pontjából az a oldalra bocsátott merőleges talppontja Ta, a b oldalra bocsátott merőleges talppontja Tb, a körrel alkotott második metszéspontja S. A B-ből induló magasság és a körülírt kör második metszéspontja R. Az s Simson egyenes P-ből vett kéteszeres nagyítása a t egyenes, ennek metszéspontjai BR-rel M, PS-sel N. PCTaTb húrnégyszög, mert Ta és Tb PC Thálesz-körén vannak. PC Ta = PCB szög egyenlő a Tb -nél lévő külső szöggel. PCB és PSB szögek is egyenlők, mint a PB húrhoz tartozó kerületi szögek. Végül s és t egyenesek párhuzamossága miatt PNM szög is az előbbiekkel egyenlő. PRBS szimmetrikus trapéz, mint a körből két párhuzamos húr által kimetszett négyszög. Az N-nél ill. S-nél lévő szögek egyenlősége miatt NPRM is szimmetrikus trapéz. t definíciója miatt PTb=TbN, a PN-re merőleges AC tehát NPRM szimmetriatengelye, így R és M egymás tükörképei AC-re. Mivel a magasságpont oldalegyenesre vett tükörképe a körülírt körön van, M az ABC  magasságpontja. t definíciója miatt t minden Q pontjára igaz, hogy a QP felezőpontja s-en van, így természetesen M-re is. magasságpontja. t definíciója miatt t minden Q pontjára igaz, hogy a QP felezőpontja s-en van, így természetesen M-re is.
|
 |
| Előzmény: [770] Bocsa Dávid, 2009-02-02 21:38:36 |
|
| [772] Bocsa Dávid | 2009-02-03 16:48:07 |
 Nagyon szép megoldás:D Köszönöm szépen. Ha esetleg tud vki másik megoldást, akkor ossza meg velem, mert tudomásom szerint több módon is bizonyítható, de egészen eddig egyre sem jöttem rá. Még egyszer köszönöm.
|
|
|
|
|
| [776] komalboy | 2009-02-12 10:57:31 |
 Sziasztok! a követekző feladatra keresek megoldást...
|
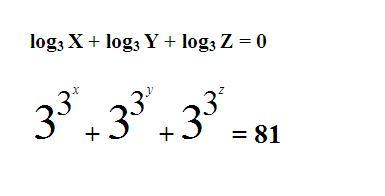 |
|
| [777] sakkmath | 2009-02-12 13:31:34 |
 Vázlatosan:
1) Az első egyenlet értelmezése.
2) Egy adott helyettesítéssel felírhatjuk a konvex függvényekre vonatkozó Jensen-egyenlőtlenséget.
3) A számtani - mértani közép összefüggésének kétszeri alkalmazása.
4) Az első pontban kapott eredménnyel kijön a megoldás.
|
| Előzmény: [776] komalboy, 2009-02-12 10:57:31 |
|
| [778] vihand | 2009-02-12 18:53:17 |
 Helló, valaki meg tudja nekem röviden írni, hogy hogy kell kinéznie egy kísérőjegyzéknek? Sajnos elhagytam az első újságot, és eddig abból néztem ki. Nem sürgős, de örülnék neki. Előre is köszönöm a segítséget.
|
|
|
| [780] MTM | 2009-02-12 19:16:49 |
 Csak úgy...:]
A feladat: C. 593. Péter a bélyeggyűjteményéből az 1,2,3,...,37 forintos bélyegek mindegyikéből kivett egy-egy darabot. Szeretné ezeket úgy csoportosítani, hogy mindegyik csoportban ugyanannyi legyen a bélyegek névértékének összege. Hányféleképpen teheti ezt meg?
Minta a dolgozatok fejlécéhez C. 593. Nagy 163 Róbert 9. évf. Győr, Révai M. Gimn. e-mail: robi@revai.hu
Jelöljük a kapitány életkorát (években kifejezve) K-val, a hajóét H-val. A hajó H-K évvel ezelőtt volt annyi idős, mint a kapitány most; akkor a kapitány K-(H-K)=2K-H éves volt. Amikor a hajó 2K-H éves lesz, akkor a kapitány ...
|
| Előzmény: [779] rizsesz, 2009-02-12 19:02:06 |
|
|
|
|
| [784] matlány | 2009-02-13 10:34:23 |
 Sakkmath!
Tényleg vázlatos, amit Ön leírt. Esetleg le tudná írni bővebben, mert érdekel ennek a megoldása. Előre is köszönöm.
|
|
| [785] Sirpi | 2009-02-13 14:49:29 |
 Ismert, hogy T=s.r=(s-a).ra=(s-b).rb=(s-c).rc
Helyettesítsük be az r-eket a bizonyítandó egyenlőségbe:

Átszorozva 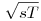 -vel és beírva a Heron-képletet ( -vel és beírva a Heron-képletet ( ), azt kapjuk, hogy ), azt kapjuk, hogy
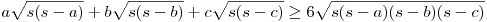
Legyen most x:=s-a, y:=s-b, z:=s-c. Ekkor a=y+z, b=x+z, c=y+z. T-vel leosztva, és ezeket beírva:
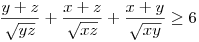
És ez igaz, mert minden tag legalább 2, hiszen minden x-re x+1/x 2, így az első tag is: 2, így az első tag is:
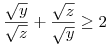
|
| Előzmény: [783] komalboy, 2009-02-13 10:16:19 |
|
| [786] laci777 | 2009-02-13 15:21:23 |
 Üdvözlet Mindenkinek!
Egy 11.-es versenyfeladat így szól: bizonyítsuk be, hogy tetszőleges konvex négyszög oldalai négyzetösszegéből annak átlói négyzetösszegét kivonva az átlók felezőit összekötő szakasz négyzetének négyszeresét kapjuk.
Megköszönnék bármilyen kiinduló pontot, gondolatot. Eddig még csak az oldal szakaszfelelők által meghatározott paralelogrammával próbálkoztam, de nem sok sikerrel (vagy nem elég kitartóan). Csak annyit tudok, hogy ez az állítás paralelogrammák esetén igaz.
Köszönöm előre is.
|
|
|
| [788] Euler | 2009-02-13 18:17:09 |
 Paralelogrammára igaz az összefüggés, igy innen adódik, hogy egy háromszög súlyvonala kiszámolható a következő módon: 4sc2=2a2+2b2-c2(csúnya, de remélem érthető). Jelöljük a négyszög csúcsait rendre A, B, C, D-vel, AC felezőpontja E, BD felezőpontja F, ekkor4EF2=2CF2+2AF2-AC2, hasonlóan CF2 és AF2 kifejezhető a DBC és DAB háromszögekből, ezekat beirva az előbbibe már adódik is az állitás. Remélem érthetően sikerült leirnom.
|
| Előzmény: [786] laci777, 2009-02-13 15:21:23 |
|
| [789] laci777 | 2009-02-13 22:18:34 |
 Kedves Euler, köszönöm szépen, érthető voltál - azt hiszem, a 3szög súlyvonalára az oldalai függvényében adott képletre az életben nem jöttem volna magamtól rá (más kérdés, még most sem nagyon látom az s(c) és az m(c) c-n való távolságának számíthatóságát - de kicsit még emésztem). Még egyszer köszönöm.
|
| Előzmény: [788] Euler, 2009-02-13 18:17:09 |
|
| [790] laci777 | 2009-02-13 22:31:43 |
 Ajjaj, már látom, s(c) és c metszésére tükrözzük C-t, így kapjuk a paralelogrammát. Késő van, egyébként is lassú vagyok:(
Még egyszer köszönöm, kellemes hétvégét.
|
|
|
|
|
| [794] laci777 | 2009-02-14 22:35:15 |
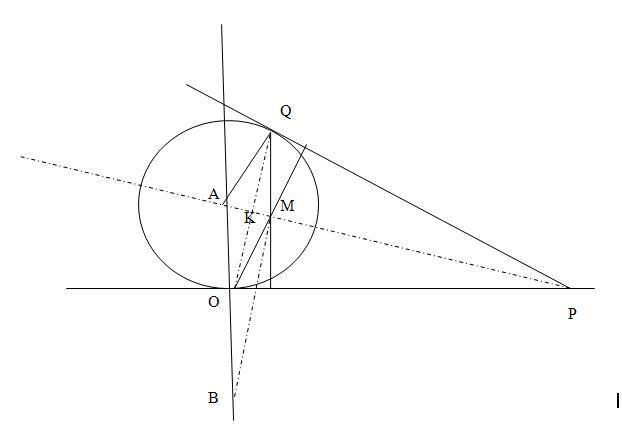
 Megint geometria-példában kérnék szépen segítséget: vegyük az x2+(y-a)2=a2 egyenletű kört (az "a" tetszőleges, de rögzített értékű pozitív valós szám). E körhöz az x tengely egy tetszőleges P pontjából érintőt húzunk (nem az origóba). Ezt az érintési pontot Q-val jelölve,határozzuk meg a PQO(O az origo) háromszög magasságpontját. Ha végighaladunk x tengely valamennyi P pontján, mit adnak ki e háromszögek magasságpontjai? Az látszik, hogy a (0;a) és a (0;-a) pontok által meghatározott szakasz Thalész-köre a megoldás a két előbbi pont nélkül - de bizonyítani már nem tudom. Tudna valaki valamilyen kiinduló pontot, ötletet javasolni? Köszönöm előre is.
|
|
| [795] HoA | 2009-02-15 07:45:55 |
 Legyen a (0;a) pont A, a (0;-a) pont B, a PQO  magasságpontja M. AQ és OM párhuzamosak, mint PQ-ra merőleges egyenesek. AO és QM párhuzamosak, mint PO-ra merőleges egyenesek. Így OMQA paralellogramma és AO = AQ ( a kör sugara ) miatt rombusz. Átlói merőlegesek, középpontját K-val jelölve AKO magasságpontja M. AQ és OM párhuzamosak, mint PQ-ra merőleges egyenesek. AO és QM párhuzamosak, mint PO-ra merőleges egyenesek. Így OMQA paralellogramma és AO = AQ ( a kör sugara ) miatt rombusz. Átlói merőlegesek, középpontját K-val jelölve AKO  derékszögű. Ezt A-ból kétszeresére nagyítva K M-be O pedig B-be kerül. AMB derékszögű. Ezt A-ból kétszeresére nagyítva K M-be O pedig B-be kerül. AMB  derékszögű, tehát M valóban AB Thálesz-körén van. derékszögű, tehát M valóban AB Thálesz-körén van.
Mivel a feladatot koordináta-geometriai megfogalmazásban tűzték ki, oldjuk meg így is. Legyen P (p;0). Q az AP átmérőjű körön van, ennek középpontja (p/2;a/2), sugara 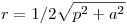 , egyenlete (x-p/2)2+(y-a/2)2=1/4(p2+a2) , (2x-p)2+(2y-a)2=p2+a2 ; 4x2-4xp+p2+4y2-4ya+a2=p2+a2 ; , egyenlete (x-p/2)2+(y-a/2)2=1/4(p2+a2) , (2x-p)2+(2y-a)2=p2+a2 ; 4x2-4xp+p2+4y2-4ya+a2=p2+a2 ;
4x2-4xp+4y2-4ya=0
Q az eredeti körön is rajta van, ennek egyenletét néggyel szorozva 4x2+4(y-a)2=4a2 ; 4x2+4y2-8ay+4a2=4a2 ;
4x2+4y2-8ay=0
A két egyenlet különbségéből a metszéspontokra y/x = p/a ( amit persze az ábráról mint OQ meredekségét könnyen leolvashatunk) , behelyettesítve 4x2+4p2x2/a2-8px=0 Egyik metszéspont az origó, erre nem vagyunk kíváncsiak, x-szel oszthatunk: x(4+4p2/a2)=8p ; x=2p/(1+p2/a2) Ez tehát Q és egyben M abszcisszája (Mx). M ordinátáját (My) abból számíthatjuk, hogy M rajta van az AP egyenesen: x/p+y/a=1 ; y=a-(a/p)x=a-2a/(1+p2/a2)=(a+p2/a-2a)/(1+p2/a2)=(p2/a-a)/(1+p2/a2) . Tekintsük az Mx2+My2 kifejezést:
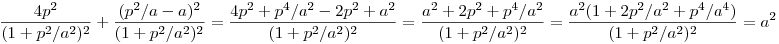 M tehát valóban az origó középpontú a sugarú körön, AB Thálesz körén van. M tehát valóban az origó középpontú a sugarú körön, AB Thálesz körén van.
|
 |
| Előzmény: [794] laci777, 2009-02-14 22:35:15 |
|
| [796] laci777 | 2009-02-15 11:20:46 |
 Kedves HoA!
Az első megoldásod egyszerű, és így nagyszerű:) A második viszont - a magam szinjéhez képest meg végképp -remekmű. Mindkettőt köszönöm!
|
| Előzmény: [795] HoA, 2009-02-15 07:45:55 |
|
| [797] Gyöngyő | 2009-02-15 12:21:18 |
 Sziasztok!
Szeretnék segítséget kérni a következő feladathoz:
Legyenek xi>0,i=1,..,n
x1+x2+...+xn=1. Igazoljuk,hogy :
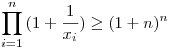
Üdv.: Gyöngyő
|
|
| [798] S.Ákos | 2009-02-15 13:56:02 |
 Legyen a+b=2p és a-b=2q, ahol a,b,p,q pozitív valós számok. Vizsgáljuk az  kifejezést. a=p+q és b=p-q. Ezekkel a helyettesítésekkel: kifejezést. a=p+q és b=p-q. Ezekkel a helyettesítésekkel:
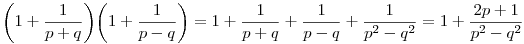
Ha 2p állandó, akkor ez a kifejezés szigorúan monoton nő a [0;p] intervallumon, ha tehát q csökken, akkor a kifejezés értéke is csökken. Ha a számok mind egyenlők, akkor 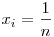 . Ha nem mind egyenlők, akkor van i,j úgy, hogy . Ha nem mind egyenlők, akkor van i,j úgy, hogy 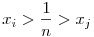 Legyen Legyen 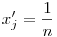 és és 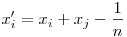 , és a többi xk-t hagyjuk változatlanul. Mivel xi+xj=xi'+xj' és xi>xj'>xj, ezért xi>xi'>xj, így xi-xj>|xj'-xi'|, így a kifejezés értéke csökkent, így a minimum csak x1=x2=...=xn esetén állhat, ami épp a jobb oldal. , és a többi xk-t hagyjuk változatlanul. Mivel xi+xj=xi'+xj' és xi>xj'>xj, ezért xi>xi'>xj, így xi-xj>|xj'-xi'|, így a kifejezés értéke csökkent, így a minimum csak x1=x2=...=xn esetén állhat, ami épp a jobb oldal.
Remélem érthető.
|
| Előzmény: [797] Gyöngyő, 2009-02-15 12:21:18 |
|
| [799] nadorp | 2009-02-15 14:17:47 |
 2. megoldás
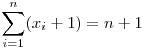 miatt a számtani és harmonikus közép közti egyenlőtlenségből miatt a számtani és harmonikus közép közti egyenlőtlenségből
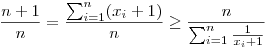 , tehát , tehát

Most felhasználva a mértani és harmonikus közép közti egyenlőtlenséget
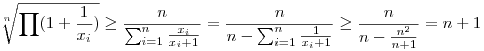
|
| Előzmény: [798] S.Ákos, 2009-02-15 13:56:02 |
|
|
| [801] sakkmath | 2009-02-16 10:19:18 |
 Ugyanez a kiinduló kör szerepel a következő feladatban is:
Adott az A(0; a) középpontú, a sugarú kör. A kör valamely - az origótól különböző - pontja legyen C. Tekintsük azokat a C-felezéspontú, OA-val párhuzamos szakaszokat, melyek hossza 2OC. Kérdések:
1. Mi a szakaszvégpontok mértani helye, ha C befutja a kört? 2. Mekkora területet zár be a mértani helyet leíró függvény görbéje? 3. Honnan lehet ismerős a kapott görbe? :)
|
| Előzmény: [795] HoA, 2009-02-15 07:45:55 |
|
|
| [803] HoA | 2009-02-17 12:53:30 |
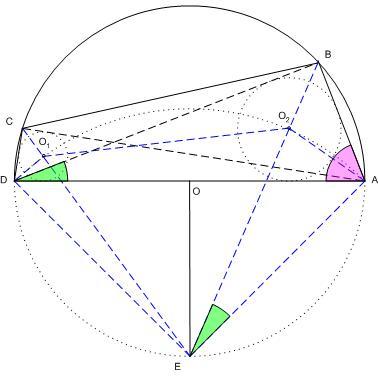
 [757] ábrája arra utal, hogy használjuk fel: a háromszög beírt körének középpontja rajta van például a b oldal  /2+ /2+ /2 látószögű körívén és az ehhez a körívhez tartozó körközéppont éppen a körülírt kör b-hez tartozó, B-t nem tartalmazó ivének felezőpontja, ahol /2 látószögű körívén és az ehhez a körívhez tartozó körközéppont éppen a körülírt kör b-hez tartozó, B-t nem tartalmazó ivének felezőpontja, ahol  szögfelezője is metszi a körülírt kört. Az itt mellékelt ábra jelöléseivel EA=EO2 egyenlőséget közvetlenül is beláthatjuk. Legyenek az ABD háromszög szögei szögfelezője is metszi a körülírt kört. Az itt mellékelt ábra jelöléseivel EA=EO2 egyenlőséget közvetlenül is beláthatjuk. Legyenek az ABD háromszög szögei  , , , , . Ekkor AEB . Ekkor AEB  = = ( BA húrhoz tartozó kerületi szög ), DAE ( BA húrhoz tartozó kerületi szög ), DAE  = DBE = DBE  = =  /2,O2 AD /2,O2 AD  = =  /2,O2 AE /2,O2 AE  = = /2+ /2+ /2 és így EAO2 háromszög O2 -nél lévő EO2A szöge is /2 és így EAO2 háromszög O2 -nél lévő EO2A szöge is  /2+ /2+ /2 , EAO2 egyenlőszárú, EA=EO2 . Ugyanez igaz EO1-re is, így O1EO2 egyenlőszárú. /2 , EAO2 egyenlőszárú, EA=EO2 . Ugyanez igaz EO1-re is, így O1EO2 egyenlőszárú.
Csak most használjuk fel, hogy egységsugarú körülírt körről és derékszögű ABD háromszögről van szó:  Az Az 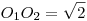 feltétel tehát azt jelenti, hogy O1EO2 feltétel tehát azt jelenti, hogy O1EO2 szabályos, O2EO1 szabályos, O2EO1 =60o , BC az egységsugarú körben 60o-os kerületi szöghöz tartozó húr, hossza így =60o , BC az egységsugarú körben 60o-os kerületi szöghöz tartozó húr, hossza így 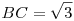
A gondolatmenet megfordítható, ha 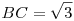 , akkor BEC , akkor BEC =O2EO1 =O2EO1 =60o , O1EO2 egyenlőszárú =60o , O1EO2 egyenlőszárú  szabályos, szabályos, 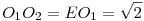
|
 |
| Előzmény: [757] BohnerGéza, 2009-01-24 16:31:35 |
|
| [804] sakkmath | 2009-02-17 13:20:30 |
 Örülök, hogy a rajzoddal talpra állítottál, az újbóli fejreállást egy tengelyes tükrözéssel megoldom :))
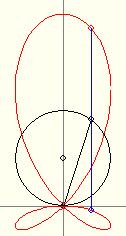
Az adott tulajdonságú pontok halmaza egy negyedrendrendű algebrai görbe (a rajzodon még két további metszéspont is bejelölhető...), melynek egyenlete - Descartes-koordinátarendszerben - implicit és explicit módon is megadható... (Utóbbi esetben a görbét több, csatlakozó ívre kell bontani.)
Egykor hosszas nyomozást folytattam annak megállapítására, hogy hol, mikor fedezték fel ezt a görbét. Az eredmény: a trifolium (lóhere) nevű görbecsalád egy speciális esetéről van szó (legalábbis ezt írta a Encyclopedia Britannica ). Az általánosabb főgörbé(ke)t egyébként nem az általam talált szerkesztéssel definiálták.
Bebizonyítható, hogy a görbe által határolt terület kétszerese a kiindulási kör területének. Nekem ez "csak" integrálszámítással sikerült. Kérdés: van-e erre egy elegánsabb módszer?
A görbével kapcsolatban több egyéb kérdés is feltehető és megválaszolható. Pl.: súlypontok, megforgatással kapott test térfogata, stb. A K kerület viszont ellenállt, ez szerintem csak közelítő módszerekkel határozható meg. Nálam K/a  14,1666. 14,1666.
|
| Előzmény: [802] BohnerGéza, 2009-02-16 19:48:30 |
|
| [805] laci777 | 2009-02-19 16:29:02 |
 Sziasztok! Most egy már megoldott(?) versenypéldával kapcsolatban kérném szépen véleményeteket.
Vegyük a köv. egyenletet: a2+b2-ab=c2 (ahol a,b,c páronként különböző pozitív valósak). A feladat: fel kell írni növekvő sorrendben a számokat. Arra jutottam, hogy egy olyan háromszög oldalairól van szó, ahol - a koszinusztétel miatt - a c oldallal szembeni szög 60 fok, és a<c<b vagy b<c<a. Ugyanakkor végtelen sok számhármas kielégíti a feltételeket (pl. 1, 2, gyökhárom ill. ezek tetszőleges k-szorosa hasonló derékszögű háromszögek esetén, és akkor még ott van végtelen sok egyéb lehetőség, ahol alfa és béta együtt 120 fok). De - ha minden igaz - ez nem jó (nem teljes?) megoldás. De miért? Tényleg szeretném tudni.
|
|
|
| [807] laci777 | 2009-02-19 19:30:30 |
 Nem tudom, jól értettem-e, amit írtál, kedves Nadorp, de pl. az (1;2;gyökhárom) számhármas esetén létezik a háromszög (bármely két oldal nagyobb a 3.-nál), és az egyenletet is kielégíti.
Vagy inkább arra utaltál, hogy a jelzett végtelen sok megoldás is csak részmegoldás, azaz létezhet olyan számhármas is, amivel az egyenlőség ugyan igaz, de háromszöget nem lehet ezekből kialakítani? Mindenesetre megpróbálok ezen is gondolkodni, mert volt kis hiányérzetem e tekintetben - de mivel a feladat azt kérte, hogy "írjuk fel növekvő sorrendben a számokat", úgy gondoltam, hogy már létező háromszögek esetén is végtelen sok megoldás adható. Ha viszont az "a", a "b" és a "c" egymáshoz képesti sorrendjét kérdezi, akkor csak a "c" köztes helyzete állapítható meg.
Vagy végképp tévúton járok?
|
| Előzmény: [806] nadorp, 2009-02-19 17:06:38 |
|
| [810] kiskiváncsi | 2009-02-19 20:24:56 |
 Kedves HOA! Ez a feladat az egyik fórumon így jelent meg: O1O2 gyök2 hosszú szakasz a Thales körbe írható derékszögű háromszögek beírt körök középpontjai körén foroghat. Mekkora a BC szakasz? Azaz ez a megadott és csak ez létezik, vagy kinetogeometriailag ki lehet szerkeszteni, BC valóban mindig gyök 3 vagy nem? Azaz ha O1,O2 szakasz forog, akkor BC állandó és egyenlő gyök3? Vagy csak ez a 6o fokhoz tartozó két szakasz együtt foroghat (merev test szerűen)?
|
|



 2. Tegyük fel, hogy p<q. Ekkor a feladatban szereplő egyenlőség úgy állhat fenn, ha p kitevője nagyobb, azaz
2. Tegyük fel, hogy p<q. Ekkor a feladatban szereplő egyenlőség úgy állhat fenn, ha p kitevője nagyobb, azaz  p<q esetén a fenti egyenlőtlenség nem állhat fenn. Marad a p=2 eset. Ekkor
p<q esetén a fenti egyenlőtlenség nem állhat fenn. Marad a p=2 eset. Ekkor 


 körülírt körének P pontjából az a oldalra bocsátott merőleges talppontja Ta, a b oldalra bocsátott merőleges talppontja Tb, a körrel alkotott második metszéspontja S. A B-ből induló magasság és a körülírt kör második metszéspontja R. Az s Simson egyenes P-ből vett kéteszeres nagyítása a t egyenes, ennek metszéspontjai BR-rel M, PS-sel N. PCTaTb húrnégyszög, mert Ta és Tb PC Thálesz-körén vannak. PC Ta = PCB szög egyenlő a Tb -nél lévő külső szöggel. PCB és PSB szögek is egyenlők, mint a PB húrhoz tartozó kerületi szögek. Végül s és t egyenesek párhuzamossága miatt PNM szög is az előbbiekkel egyenlő. PRBS szimmetrikus trapéz, mint a körből két párhuzamos húr által kimetszett négyszög. Az N-nél ill. S-nél lévő szögek egyenlősége miatt NPRM is szimmetrikus trapéz. t definíciója miatt PTb=TbN, a PN-re merőleges AC tehát NPRM szimmetriatengelye, így R és M egymás tükörképei AC-re. Mivel a magasságpont oldalegyenesre vett tükörképe a körülírt körön van, M az ABC
körülírt körének P pontjából az a oldalra bocsátott merőleges talppontja Ta, a b oldalra bocsátott merőleges talppontja Tb, a körrel alkotott második metszéspontja S. A B-ből induló magasság és a körülírt kör második metszéspontja R. Az s Simson egyenes P-ből vett kéteszeres nagyítása a t egyenes, ennek metszéspontjai BR-rel M, PS-sel N. PCTaTb húrnégyszög, mert Ta és Tb PC Thálesz-körén vannak. PC Ta = PCB szög egyenlő a Tb -nél lévő külső szöggel. PCB és PSB szögek is egyenlők, mint a PB húrhoz tartozó kerületi szögek. Végül s és t egyenesek párhuzamossága miatt PNM szög is az előbbiekkel egyenlő. PRBS szimmetrikus trapéz, mint a körből két párhuzamos húr által kimetszett négyszög. Az N-nél ill. S-nél lévő szögek egyenlősége miatt NPRM is szimmetrikus trapéz. t definíciója miatt PTb=TbN, a PN-re merőleges AC tehát NPRM szimmetriatengelye, így R és M egymás tükörképei AC-re. Mivel a magasságpont oldalegyenesre vett tükörképe a körülírt körön van, M az ABC 

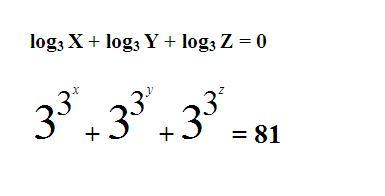

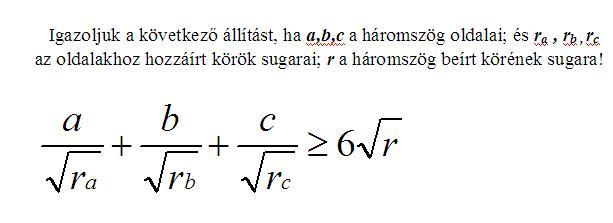







 /2+
/2+ /2 látószögű körívén és az ehhez a körívhez tartozó körközéppont éppen a körülírt kör b-hez tartozó, B-t nem tartalmazó ivének felezőpontja, ahol
/2 látószögű körívén és az ehhez a körívhez tartozó körközéppont éppen a körülírt kör b-hez tartozó, B-t nem tartalmazó ivének felezőpontja, ahol  ,
, . Ekkor AEB
. Ekkor AEB  =
=
 14,1666.
14,1666.