| [811] nadorp | 2009-02-19 23:10:40 |
 Én a bizonyításod megfogalmazására gondoltam.
Ha azt mondod:
"Tekintsünk egy a,b,c oldalú háromszöget, melyre fennáll az egyenlőség. Ekkor a cosinus tétel szerint ebben a háromszögben a c-vel szemben 60o van, tehát c a "középső" hosszúságú oldal."
akkor a fenti bizonyítás hiányos, mert nem tudjuk, hogy létezik-e az a,b,c oldalú háromszög.
Ha viszont azt mondod:
"Tekinsünk két pozitív a b számot és nézzük azt a háromszöget, melynek két oldala a és b, közbezárt szögük 60o. Ez egyértelműen meghatározza a c oldal hosszát és az egyenlőség összes megoldását megkaphatjuk ezzel a módszerrel. Mivel ezek a háromszögek nem szabályosak és c a "középső" hosszúságú oldal, ezért a<c<b vagy b<c<a teljesülhet." b számot és nézzük azt a háromszöget, melynek két oldala a és b, közbezárt szögük 60o. Ez egyértelműen meghatározza a c oldal hosszát és az egyenlőség összes megoldását megkaphatjuk ezzel a módszerrel. Mivel ezek a háromszögek nem szabályosak és c a "középső" hosszúságú oldal, ezért a<c<b vagy b<c<a teljesülhet."
akkor jó a megoldásod.
|
| Előzmény: [807] laci777, 2009-02-19 19:30:30 |
|
| [812] jenei.attila | 2009-02-19 23:22:26 |
 Van-e a valós számok additív csoportjának nem triviális automorfizmusa?
Van-e a valós számok testének véges, vagy megszámlálható indexű részteste? Egyáltalán continuum számosságú valódi részteste? Mi a "legbővebb" valódi résztest?
Nem tudom a válaszokat, valaki segíthetne.
|
|
|
| [814] HoA | 2009-02-20 10:29:29 |
 Ha az a bizonyos Thálesz-kör egységsugarú és a "Thales körbe írható derékszögű háromszögek beírt körök középpontjai köre" [803] ábrájának AO2O1D körívét jelenti, O1ésO2 pedig az ACD ill. ABD háromszögek beírt köreinek középpontját, akkor az első válasz igen, BC mindig gyök 3. Ugyanis a körív sugara 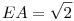 , ezért ebben az esetben EO1O2 háromszög szabályos, E-nél lévő szöge 60o. Mivel az EO1ésEO2 egyensek egyúttal a C-nél ill. B-nél lévő derékszögek felezői, így az általuk bezárt szög 60o, tehát BC az egységsugarú körnek 60o-os kerületi szöghöz tartozó húrja, ez pedig , ezért ebben az esetben EO1O2 háromszög szabályos, E-nél lévő szöge 60o. Mivel az EO1ésEO2 egyensek egyúttal a C-nél ill. B-nél lévő derékszögek felezői, így az általuk bezárt szög 60o, tehát BC az egységsugarú körnek 60o-os kerületi szöghöz tartozó húrja, ez pedig  hosszú. hosszú.
Ha O1O2 forog, BC is mozog, de nem együtt, "merev test szerűen" forognak. [755] és [803] ábrájának összehasonlításából látható, hogy szimmetrikus esetben O1O2 és BC párhuzamosak, egyébként nem. Szemléletesen úgy képzelhető, hogy a rögzítetten 60o-os O2EO1 szög két szára forog legyezőszerűen, és bármely helyzetében a 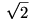 sugarú AO2O1D körívből 60o-os középponti szöghöz tartózó sugarú AO2O1D körívből 60o-os középponti szöghöz tartózó 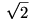 hosszúságú O1O2 húrt, az egységsugarú Thálesz-körből pedig 60o-os kerületi szöghöz tartózó hosszúságú O1O2 húrt, az egységsugarú Thálesz-körből pedig 60o-os kerületi szöghöz tartózó  hosszúságú BC húrt metsz ki. hosszúságú BC húrt metsz ki.
|
| Előzmény: [810] kiskiváncsi, 2009-02-19 20:24:56 |
|
| [815] laci777 | 2009-02-22 00:21:36 |
 Ha nem baj, megint egy példával jönnék, kifogni látszik rajtam. Egy egyenletes v1 sebességgel haladó, 1 km hosszú menetoszlop végéről t0 időpontban egy futár szintén egyenletes v2 sebességgel az oszlop legelejére megy. Ott 15 mp-ig az oszloppal halad, majd az eredeti v2 sebességével az oszlop végére visszamegy. Mire visszaér, a folyamatosan haladó menetoszlop t0 időponttól pont 1 km-t tesz meg. A kérdés, mekkora utat tett meg a futár összesen?
Azt látom, hogy a 15 mp-ben megtett, 0<s<1 km út függvényében egyre nagyobb a szükséges v2-v1 sebességkülönbség, ill. hogy a futár összteljesítménye 2 és 3 km (pontosabban 1+gyökkető és 3) km között kell legyen, de a megoldáshoz vezető másodfokú egyenlet (legalábbis nagyon remélem, hogy az) túl kemény dió:(
Még az itt felvetett többi probléma nehézségét látva is remélem, most is lesz, aki segít a megoldásban:)
Előre is köszönöm.
|
|
| [816] M. Feri | 2009-02-22 12:54:29 |
 Sziasztok! A következő feladatban valami hiba van, vagy én vagyok figyelmetlen? (Szerintem hiányzik még egy feltétel): Ha f és g [a,b] intervallumot leképezi a valós számok halmazára, mindkét függvény konvex, deriválható és deriváltjai folytonosak, emellett még f(x) g(x) akkor g(x) akkor 
Megoldható így, ebben az alakban? Ha igen, hogy? Előre is köszönöm!!
|
|
|
|
| [819] plac | 2009-02-22 14:22:15 |
 Hello! A kérdésem a következő lenne. Valaki megtudja nekem mondani, hogy fn(x)=x.arctan(nx), H=(0, ) függvénysorozat egyenletesen konvergens-e a konvergencia halmazán és hogy ezt hogyan bizonyítom... Bocsánat ha valaki nagyon bugyutának véli a kérdést, de nagyon nem látom, hogy kellene megcsinálni. ) függvénysorozat egyenletesen konvergens-e a konvergencia halmazán és hogy ezt hogyan bizonyítom... Bocsánat ha valaki nagyon bugyutának véli a kérdést, de nagyon nem látom, hogy kellene megcsinálni.
|
|
| [820] Lóczi Lajos | 2009-02-22 17:23:04 |
 Viszont igazzá válik az állítás, ha megköveteljük, hogy a két végpontban ugyanazok legyenek a függvényértékek, vagyis f(a)=g(a) és f(b)=g(b) legyen.
Ekkor ugyanis a két konvex alakzat tartalmazni fogja egymást (az egyik alakzat a két végpont, az őket összekötő szakasz és f "lelógó" grafikonja által határolt síkidom; a másik ugyanígy, csak g-vel), és ismert (itt a Fórumon már kétszer is előkerült a bizonyítása, csak meg kell keresd :), hogy ha egy konvex alakzat tartalmaz egy másikat, akkor a külső alakzat kerülete nem lehet kisebb.
|
| Előzmény: [818] M. Feri, 2009-02-22 13:45:13 |
|
| [821] Lóczi Lajos | 2009-02-22 18:20:58 |
 Rögzített x H-ra n H-ra n  esetén fn(x) esetén fn(x) f(x):= f(x):= x/2. A függvénysorozat egyenletes konvergenciája azt jelenti, hogy x/2. A függvénysorozat egyenletes konvergenciája azt jelenti, hogy  . Ezt kell igazolni most. Ehhez egy kis függvényvizsgálatra van szükség. . Ezt kell igazolni most. Ehhez egy kis függvényvizsgálatra van szükség.
1. Látszik, hogy ha x rögzített, akkor a konvergencia n-ben monoton: fn(x)<fn+1(x)<f(x), vagyis |fn(x)-f(x)|=f(x)-fn(x)=:gn(x).
2. Pl. L'Hospital-lal belátod, hogy  illetve két deriválással, hogy gn(x) konkáv. De gn(0)=0 is igaz. Vagyis rögzített n-re gn olyan nemnegatív konkáv függvény, amely 0-ban 0, a végtelenben pedig a határértéke pozitív. Egy ilyen függvény viszont minden x illetve két deriválással, hogy gn(x) konkáv. De gn(0)=0 is igaz. Vagyis rögzített n-re gn olyan nemnegatív konkáv függvény, amely 0-ban 0, a végtelenben pedig a határértéke pozitív. Egy ilyen függvény viszont minden x H esetén kisebb, mint a limesze, tehát H esetén kisebb, mint a limesze, tehát 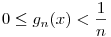 , minden x-re és n-re. , minden x-re és n-re.
3. Emiatt 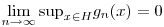 . .
|
| Előzmény: [819] plac, 2009-02-22 14:22:15 |
|
| [822] HoA | 2009-02-23 10:08:45 |
 Szerintem a feladatban nem az okozza a gondot, hogy „a megoldáshoz vezető másodfokú egyenlet túl kemény dió” , hanem az, hogy a feladat egy kicsit tisztességtelenül van kitűzve. Az egyik szokásos középiskolai feladattípus szövegében megadnak bizonyos paramétereket és az eredményt ezek függvényében várják. Ha zárójelben megadják a paraméterek numerikus értékét is, akkor ezeket az eredmény képletébe behelyettesítve számszerű eredményt is tudunk adni . Másik fekadattípus az, ahol egy fizikai jelenség kapcsán bizonyos mennyiségek közötti összefüggések keresése, értékhatárok megállapítása a cél. Itt a kettő keveredik, a baj csak az, hogy ez a szövegből nem derül ki egyértelműen. Tisztességesnek valahogy így érezném a feladat kitűzését:
Egy egyenletes v1 sebességgel haladó menetoszlop végéről t0 időpontban egy futár szintén egyenletes v2 sebességgel az oszlop legelejére megy. Ott 15 mp-ig az oszloppal halad, majd az eredeti v2 sebességével az oszlop végére visszamegy. Mire visszaér, a folyamatosan haladó menetoszlop t0 időponttól pont 1 km-t tesz meg. A kérdés, mekkora utat tett meg a futár összesen? Milyen összefüggés áll fenn v1 és v2 között, ha tudjuk, hogy a menetoszlop 1 km hosszú?
Megoldás: A futár teljes menetideje 1000/v1 mp, ebből 15 mp-ig v1, egyébként v2 sebességgel haladt, a megtett út tehát s =  méter. A v1ésv2 közötti összefüggést abból állapítjuk meg, hogy a futár 1000/v1-15 mp alatt az 1000 méteres oszlop végéről az elejére majd vissza ment, menetideje tehát: méter. A v1ésv2 közötti összefüggést abból állapítjuk meg, hogy a futár 1000/v1-15 mp alatt az 1000 méteres oszlop végéről az elejére majd vissza ment, menetideje tehát: 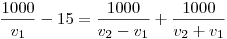 Ezek után a v2-re adódó másodfokú egyenletet elemezhetjük, milyen v1 értékekre kapunk pozitív v2-t, v2 milyen határok között változhat, stb. Végül v2-t v1 függvényeként felírva behelyettesíthetjük a megtett út képletébe, így az egy csak v1 -től függő kifejezés lesz, de továbbra sem egy konkrét számérték. Ezek után a v2-re adódó másodfokú egyenletet elemezhetjük, milyen v1 értékekre kapunk pozitív v2-t, v2 milyen határok között változhat, stb. Végül v2-t v1 függvényeként felírva behelyettesíthetjük a megtett út képletébe, így az egy csak v1 -től függő kifejezés lesz, de továbbra sem egy konkrét számérték.
|
| Előzmény: [815] laci777, 2009-02-22 00:21:36 |
|
| [823] laci777 | 2009-02-23 16:53:01 |
 Kedves HoA!
Köszönet (ismét) a segítségért. Úgy gondoltam eredetileg, hogy az egyes időintervallumokban megtett utakkal operálok, de boncolás (+eltévedés:() lett sajna belőle...
Még egyszer köszönöm szépen.
|
| Előzmény: [822] HoA, 2009-02-23 10:08:45 |
|
| [824] Káli gúla | 2009-02-23 19:14:32 |
 Működik az is. Legyen v2=kv1, a menetoszlop hossza M. Amíg fel- és lefut, addig 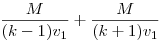 idő telik el, ez alatt a menet idő telik el, ez alatt a menet 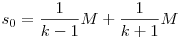 , a futár pedig , a futár pedig 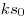 utat tesz meg. A középső időszakban együtt mennek, ez a feltétel miatt utat tesz meg. A középső időszakban együtt mennek, ez a feltétel miatt 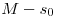 , tehát a futár összesen , tehát a futár összesen 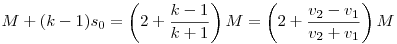 utat tett meg a feladat adataival (akkor is, ha 15 mp-ig megy elöl, és akkor is, ha 100 órát vagy ha 0 mp-et ment volna). utat tett meg a feladat adataival (akkor is, ha 15 mp-ig megy elöl, és akkor is, ha 100 órát vagy ha 0 mp-et ment volna).
|
| Előzmény: [823] laci777, 2009-02-23 16:53:01 |
|
| [825] laci777 | 2009-02-23 23:22:06 |
 Kedves Káli Gúla!
Köszönöm szépen ezt a megoldást is, bár őszintén szólva olyat igyekeztem volna kiizzadni (a jelzett eredménnyel:(), ahol a menetoszlop (a példa adatai szerint 0<v1<240 km/h közt értelmezhető) sebessége az egyedüli független változó, ahogyan valóban is annak a függvénye minden egyéb tényező (a v2 és az egyes szakaszok s és t értékei egyaránt). Még egyszer köszönöm.
|
| Előzmény: [824] Káli gúla, 2009-02-23 19:14:32 |
|
| [826] tudniakarok | 2009-02-24 13:46:11 |
 Sziasztok! Kérlek segítsetek!
Az a problémám, hogyha adott tetszőleges db nemnegatív szám, akkor hogyan tudnám elrendezni őket egy mátrixba úgy hogy a lehető legegyenletesebb elrendezést kapjam.(Arra gondolván, hogy a két legnagyobb szám a "legtávolabb" legyen egymástól, és így tovább...) Van-e erre vmilyen már kidolgozott algoritmus, mert nem nagyon találom a szakirodalmakban!? Van ötletem, de elég egyszerűnek találom ráadásul nagy számításigényű,hátha vki tud jobbat!
Előre is köszi a segítséget!
|
|
| [827] HoA | 2009-02-24 14:08:59 |
 Köszönöm Káli gúla szép megoldását. Azt hiszem, segít még jobban rávilágítani arra, mi a bajom ezzel a feladattal. Fussunk tehát neki harmadszor is, ezúttal az ő jelöléseit is használva:
Egy egyenletes v1 sebességgel haladó, M méter hosszú menetoszlop végéről t0 időpontban egy futár szintén egyenletes v2 sebességgel az oszlop legelejére megy. Ott t mp-ig az oszloppal halad, majd az eredeti v2 sebességével az oszlop végére visszamegy. Mire visszaér, a folyamatosan haladó menetoszlop t0 időponttól pont M métert tesz meg. A kérdés, mekkora utat tett meg a futár összesen? ( Számadatok: t = 15 s , M = 1000 m )
A futár megtett útja [822] megoldóképlete szerint így alakul:
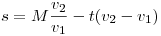 | (1) |
Mint az várható volt, a megtett út a feladatban szereplő M,t,v1ésv2 mennyiségektől függ. M és t konkrét értéke adott, de v1ésv2 szerepét jótékony homály fedi. Gondolhatnánk, hogy azok is az M és t ismeretében értelmes határok között szabadon megadhatók, csak most éppen nem rendelünk hozzájuk számértéket. De ez nem így van. A feladat túlhatározott, adott M és t mellett már v1ésv2 nem választható meg egymástól függetlenül. Az adatok közötti megkötést éppen [822] feltételi egyenlete adja:
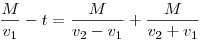 | (2) |
Ha M,v1ésv2 értéke lenne adott, megtehetnénk, hogy (2) –ből kifejezzük t-t és ezt behelyettesítjük (1) –be. Rövid átalakítások után [824] szép képletét kapjuk:
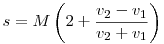 | (3) |
De az ekkor sem lenne igaz, hogy „akkor is, ha 15 mp-ig megy elöl, és akkor is, ha 100 órát”, hiszen egy adott M,v1ésv2 hármashoz egy konkrét, éppen a (2) egyenletből adódó t érték tartozik.
Nekünk azonban Mést adott. Mit tehetünk, hogy bemenő adatainktől egyértelműen függő eredményt kapjunk? Az egyik megoldás laci777 „izzadási iránya”: (2) –ből v2-re másodfokú egyenletet kapunk. Ennek fizikailag értelmes gyökét választva v2 -nek ezt a kifejezését behelyettesítjük (1) –be és kapunk egy csúnya , de csak M-et,t-tésv1-et tartalmazó kifejezést. A másik megoldás az, hogy elfogadjuk (3) szép képletét megoldásnak, de hozzátesszük, hogy „ahol v1 szabadon választott sebesség a 0<v1<M/t tartományban, v2 pedig a (2) feltételből számított M,t,ésv1 által meghatározott sebesség”. És ekkor persze a (3) képletben szereplő mennyiségekhez éppen a megadott t érték trtozik.
|
| Előzmény: [824] Káli gúla, 2009-02-23 19:14:32 |
|
|
| [829] laci777 | 2009-02-24 16:15:51 |
 Én köszönöm, mégpedig Neked, valamint Káli Gúlának a hasznos útmutatást. Túl azon, hogy egy magamban már eléggé reménytelennek elkönyvelt problémában segítettetek, élvezet volt számomra a gondolatmeneteteket is követni.
A gordiusi csomó átvágását - tekintettel a valóban csúnya paraméteres megoldásra - külön is köszönöm:)
Szép napot: Laci
|
| Előzmény: [827] HoA, 2009-02-24 14:08:59 |
|
| [830] fityfiritty | 2009-02-25 12:48:20 |
 Sziasztok, remek ez a Fórum, le a kalappal! A sok érdekes, okos hozzászólás felbátorított, hogy tőletek kérjek segítséget ehhez a feladathoz: Az (an) sorozat elemeit így definiáljuk:
a0 = 1; a1 = 0; 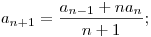 ha n = 1, 2, .... . Konvergens-e az (an) sorozat? Ha igen, akkor mi a határértéke? ha n = 1, 2, .... . Konvergens-e az (an) sorozat? Ha igen, akkor mi a határértéke?
Köszi szépen, előre is!
|
|
| [831] jonas | 2009-02-25 13:45:05 |
 Az ilyen fajta feladatra van egy általános módszer, ami gyakran működik. Számold ki a rekurziós szabályból a sorozat első néhány elemét pontosan. Keress rá a számlálójukra az OEIS-ben, megtalálod az A053557 sorozatot egyetlen találatként. Ennek a leírása azt mondja, hogy a sorozat n-ik eleme a 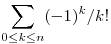 szám számlálója, ebből megsejted, hogy a te an sorozatod általános tagja éppen ez az összeg lesz, de vigyázz, az index eggyel el van csúsztatva! Ellenőrzöd, hogy ez a sejtés igaz-e az első néhány tagra, aztán ha igen, akkor megpróbálod belátni teljes indukcióval, hogy ez az explicit képlet valóban mindig igaz. Ezután már csak be kell látnod, hogy ez hova konvergál. szám számlálója, ebből megsejted, hogy a te an sorozatod általános tagja éppen ez az összeg lesz, de vigyázz, az index eggyel el van csúsztatva! Ellenőrzöd, hogy ez a sejtés igaz-e az első néhány tagra, aztán ha igen, akkor megpróbálod belátni teljes indukcióval, hogy ez az explicit képlet valóban mindig igaz. Ezután már csak be kell látnod, hogy ez hova konvergál.
|
| Előzmény: [830] fityfiritty, 2009-02-25 12:48:20 |
|
|
| [833] HoA | 2009-02-25 16:40:55 |
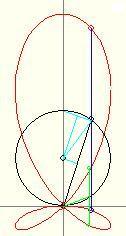
 Ha a választott abszcisszához tartozó két másik metszéspontot is bejelöljük ( zöld szakasz végpontjai ) és a görbe által határolt területet integrálszámítással, a görbe alatti területek különbségeként számítjuk, az x tengely alatti értékeket szokás szerint negatívnak véve, akkor eredményül a nagy levél területének és a két kis levél területének különbségét kapjuk. Ha OC az y tengellyel  szöget zár be, a kis kék háromszögekből az infinitezimális területdarab szöget zár be, a kis kék háromszögekből az infinitezimális területdarab  Td=4a(cos Td=4a(cos -sin -sin )2acos2 )2acos2   , amiből a teljes terület , amiből a teljes terület
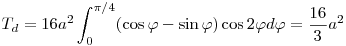
Érdekes, hogy ez a terület a2-nek racionális számszorosa. Elfogadva, hogy a területek abszolút értékének összege
Ts=2 a2 a2
, a felső levél területét T1-gyel, a két kis levél területének összegét T2 -vel jelölve
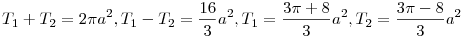
A számértékeket behelyettesítve azt kapjuk, hogy T1 nagyjából 92,5 , T1 pedig 7,5 százaléka a teljes területnek. ( ha jól számoltam ... :-) )
|
 |
| Előzmény: [804] sakkmath, 2009-02-17 13:20:30 |
|
|
|
|
|
|
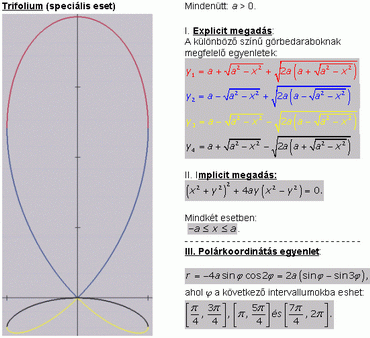
| [839] sakkmath | 2009-02-26 12:20:11 |
 Az egyes levelek területeire én is ezeket az eredményeket kaptam. Levezetésedben a teljes területre, mint adott értékre támaszkodsz. Hogy ez a szál se legyen elvarratlan, felteszem az alábbi ábrát, amely további adatokat szolgáltat a görbéről. Így bárki összevetheti saját eredményeit az általam közöltekkel... .
|
 |
| Előzmény: [833] HoA, 2009-02-25 16:40:55 |
|
| [840] fityfiritty | 2009-02-26 17:01:02 |
 Nagyon jó!! Köszönöm Neked is és Jonasnak is a profi, klassz válaszokat, tanácsokat. Most már meg merem kockáztatni, hogy az ex hatványsorának az x = -1- hez tartozó részletösszegéhez jutottunk, ha nem tévedek. Ezért a limeszre a tippem: 1/e. Üdvözöl mindenkit: fityfiritty.
|
| Előzmény: [832] nadorp, 2009-02-25 15:50:24 |
|
| [841] pvong17 | 2009-03-01 15:21:48 |
 Ha egy nem szimmetrikus mátrixnak, létezik negatív sajátértéke akkor már nem is lehet pozitív definit, ugye ?
(bocsánat ha triviális)
|
|
|
|
|
| [845] pvong17 | 2009-03-02 00:00:39 |
 Én kérek bocsánatot. Nem irtam le pontosan a feladatot és megzavart egy másik feladat. (Konkrétan Obádivics Gy. Lináris algebra -zöld könyv- 258.o 3.példája, ami ezek szerint hibás , mert egy nem szimm mátrixról(valós) állitja hogy poz defeinit, majd utána be is bizonyitja ezt :) )
Most már nincs probléma, mert sikerült letisztáznom a dolgokat. Köszönöm a gyors reakciót.
|
| Előzmény: [844] Lóczi Lajos, 2009-03-01 20:46:41 |
|
| [846] nadorp | 2009-03-02 10:51:34 |
 A pozitív definitséghez szerintem nem kell szimmetrikus mátrix. Egy valós nXn A mátrix pozitív definit, ha minden x=(x1,...,xn) vektorra xTAx>0. Az már egy másik dolog, hogy kvadratikus alakok definitségének vizsgálatához már szimmetrikus mátrixokkal dolgozunk, mert az egyszerűbb.
Van egy egy tétel is, mely szerint egy A mátrix pozitív definit akkor és csak akkor ha a  mátrix pozitív definit (http://mathworld.wolfram.com/PositiveDefiniteMatrix.html). Úgy hogy az az Obádovics példa nem biztos hogy hibás. mátrix pozitív definit (http://mathworld.wolfram.com/PositiveDefiniteMatrix.html). Úgy hogy az az Obádovics példa nem biztos hogy hibás.
|
| Előzmény: [845] pvong17, 2009-03-02 00:00:39 |
|
|
|
|
| [850] akinom91 | 2009-03-06 22:33:50 |
 Kérem, valaki segítsen megoldani a c.) pontot, esetleg az a.) pontot Cayley-Hamilton összefüggéssel (nekem csak egyszerű számítással sikerült). Előre is köszönöm!
|
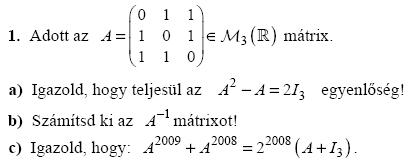 |
|
| [851] jonas | 2009-03-06 22:50:12 |
 A (c) pontot többféleképp is meg lehet közelíteni. Az egyik lehetőség, hogy az A mátrixot Jordan blokk alakra hozod, és ezt hatványozod.
A másik, hogy felhasználod az (a) pontot, amely szerint A2=A+2I ami alapján A3=A(A2)= A(A+2I)=A2+2A=3A+2I. Ebből megsejted, hogy az általános hatvány felírható An=pnA+qnI alakban. Valóban: An+1=A.An= A(pnA+qnI)=pnA2+qnA= (pn+qn)A+2pnI. Ebből pn+1=pn+qn, és qn=2pn, amiből pn+1=pn+2pn-1. A kezdeti feltétel is nyilván teljesül: p0=0,q0=1, p1=1,q1=0. (Persze ellenőrizned kell, hogy nem számoltam el.) Ennek a rekurziónak megkeresheted az explicit képletét. (Ez elvileg nem, csak gyakorlatban egyszerűbb annál, mintha az An mátrix mind a kilenc elemére írnál föl együttes lineáris rekurziót.)
|
| Előzmény: [850] akinom91, 2009-03-06 22:33:50 |
|
| [852] akinom91 | 2009-03-06 23:19:33 |
 Hát sajnos az első megoldásodnál fogalmam sincs, miről beszélsz, a másodikat meg nagyjából értem, amennyit leírtál (én is valami képletet próbáltam keresni). Meglátjuk, sikerül-e explicit képletet találni, ugyanis még ilyet nem oldottam, és nem tudom mennyire lehet gimnáziumi szinten... . És akkor a képletet amit feltételezzük, hogy megkapok, kell még bizonyítani mat. ind. módszerével, vagy ez már megvolt? :D Köszi a tippet az elinduláshoz, remélem érettségiig már kívülről fújom a típusfeladatok megoldásainak módszerét. :)
|
| Előzmény: [851] jonas, 2009-03-06 22:50:12 |
|
| [853] Káli gúla | 2009-03-07 00:54:41 |
 Ha E-vel jelölöd a csupa egyesekből álló mátrixot, akkor A=E-I, tehát A2+A=(E2-2E+I)+(E-I)=E2-E, ami a csupa kettesekből álló mátrix, ezért A2+A=2E=2(A+I). Ez ugyanaz, mint az a), és ebből A-val szorzással, indukcióval adódik a c) is.
|
| Előzmény: [852] akinom91, 2009-03-06 23:19:33 |
|
| [854] akinom91 | 2009-03-07 13:03:18 |
 Köszönöm szépen mind a két megoldási módot, sikerült az explicit képletet is megkapni (igaz, segítséggel, még életemben ilyet nem csináltam). A lényeg, hogy mind a 2 hasznos volt, tanultam valami újat, csak máskor is fel tudjam magamtól is használni. Ha már itt tartunk valaki fel tudná nekem írni, hogy a Fibonacci-féle sorozatot, hogy kell megadni explicit módon? Ezt kaptam:
Fibonacci sorozat: apn+1=bpn+cpn-1
Karakterisztikus egyenlet: aR2=bR+c; R1, R2 a karakterisztikus egyenlet megoldásai.
Ha R1=R2 => pn=R1n(A+nB); Ha R1 R2 => pn=R1nA+R2nB; (Ha valamit elírtam, javítsatok!) R2 => pn=R1nA+R2nB; (Ha valamit elírtam, javítsatok!)
Ott akadtam meg, ha a karakt. egyenlet esetében  <0. Ilyen esetben, hogy lehet felírni az explicit képletet? <0. Ilyen esetben, hogy lehet felírni az explicit képletet?
Előre is köszi!
|
| Előzmény: [853] Káli gúla, 2009-03-07 00:54:41 |
|
|
| [856] Lóczi Lajos | 2009-03-08 20:00:58 |
 Ha a diszkrimináns kisebb nullánál, a képlet formálisan ugyanaz, csak konjugált komplex számokat tartalmaz (amelyek együttesen valós értéket adnak). De az Euler-összefüggésekkel ezt az esetet mindig átírhatod exponenciális függvényt és szinuszt/koszinuszt tartalmazó alakra, amiben már csak valós számok vannak.
|
| Előzmény: [854] akinom91, 2009-03-07 13:03:18 |
|
| [857] Lóczi Lajos | 2009-03-08 20:49:07 |
 Itt minden bizonnyal két dolgot érdemes összekombinálni: van egy képlet az integrálfüggvény Fourier-együtthatóinak kiszámítására (az eredeti függvény Fourier-együtthatóiból), így elég csak a logaritmus és a kotangens függvény kompozíciójának meghatározni a sorfejtését. (A függvény paritása miatt az egyik paritású együtthatók nullák lesznek.) A kotangenset szétbontva, lényegében ln (cos ).sin , ln (cos ).cos , ln (sin ).cos , ln (sin ).sin integrandusú határozott integrálok maradnak (az argumentumokban persze a megfelelő helyeken ott a szumma futóindexe). Ezeket az integrálokat ki lehet számolni (persze az integrandus nem korlátos volta miatt az integrálok konvergenciáját ellenőrizni kell), egyszer kiszámítottam őket, de csak elég trükkösen jöttek ki. (Utólag aztán látható volt, hogy az a feladat a 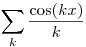 és és  függvénysorok összegével van kapcsolatban, amelyeket egyszerűbben egy függvénysorok összegével van kapcsolatban, amelyeket egyszerűbben egy 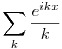 komplex exponenciális sor összegeként volt érdemes kiszámolni.) Szóval esetleg próbálj meg ezeket a nyomokon elindulni; mindenesetre a direkt számolások nem lesznek egyszerűek. komplex exponenciális sor összegeként volt érdemes kiszámolni.) Szóval esetleg próbálj meg ezeket a nyomokon elindulni; mindenesetre a direkt számolások nem lesznek egyszerűek.
|
| Előzmény: [855] plac, 2009-03-07 16:12:53 |
|
|
|
| [860] gubanc | 2009-03-13 12:41:36 |
 Nagyrabecsült FÓRUMOSOK! Sehogy sem bírok ezzel a feladattalÿ:( segítenétek?
Legyenek n és k adott pozitív egészek és tekintsük azon f: {1; 2; 3; ...; n}  {-k; -k+1; ...; k-1; k} függvényeket, amelyekre |f(i) - f(j)| {-k; -k+1; ...; k-1; k} függvényeket, amelyekre |f(i) - f(j)| k bármely i, j k bármely i, j {1; 2; 3; ...; n} esetén. Hány ilyen f függvény van? {1; 2; 3; ...; n} esetén. Hány ilyen f függvény van?
Üdv: gubanc
|
|



 b számot és nézzük azt a háromszöget, melynek két oldala a és b, közbezárt szögük 60o. Ez egyértelműen meghatározza a c oldal hosszát és az egyenlőség összes megoldását megkaphatjuk ezzel a módszerrel. Mivel ezek a háromszögek nem szabályosak és c a "középső" hosszúságú oldal, ezért a<c<b vagy b<c<a teljesülhet."
b számot és nézzük azt a háromszöget, melynek két oldala a és b, közbezárt szögük 60o. Ez egyértelműen meghatározza a c oldal hosszát és az egyenlőség összes megoldását megkaphatjuk ezzel a módszerrel. Mivel ezek a háromszögek nem szabályosak és c a "középső" hosszúságú oldal, ezért a<c<b vagy b<c<a teljesülhet." 
 g(x) akkor
g(x) akkor 
 ) függvénysorozat egyenletesen konvergens-e a konvergencia halmazán és hogy ezt hogyan bizonyítom... Bocsánat ha valaki nagyon bugyutának véli a kérdést, de nagyon nem látom, hogy kellene megcsinálni.
) függvénysorozat egyenletesen konvergens-e a konvergencia halmazán és hogy ezt hogyan bizonyítom... Bocsánat ha valaki nagyon bugyutának véli a kérdést, de nagyon nem látom, hogy kellene megcsinálni. H-ra n
H-ra n
 x/2. A függvénysorozat egyenletes konvergenciája azt jelenti, hogy
x/2. A függvénysorozat egyenletes konvergenciája azt jelenti, hogy 

 szöget zár be, a kis kék háromszögekből az infinitezimális területdarab
szöget zár be, a kis kék háromszögekből az infinitezimális területdarab  Td=4a(cos
Td=4a(cos
 ) tetszőleges mértéktér,s legyen f
) tetszőleges mértéktér,s legyen f




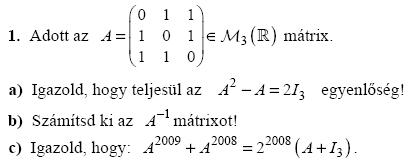
 ,
,