|
| [1670] jenei.attila | 2012-02-19 17:49:47 |
 A 2. kérdésedre válaszolva: Egyik sem igaz. Ha pl. egy nem egyenlő szárú háromszöget a legkisebb szögű csúcsa körül 120, illetve 240 fokkal elforgatunk, akkor egy olyan alakzatot kapunk ami se középpontosan, se tengelyesen nem szimmetrikus. Középpontosan akkor lenne szimmetrikus egy alfa szögű elforgatásra nézve szimmetrikus alakzat (feltéve hogy az alakzat nem egyetlen pont), ha léteznének n és m természetes számok, hogy n/m*alfa=180 fok, ahol m páratlan (tehát nem kell, hogy alfa osztója legyen 180-nak, mint ahogy Lórántfy áll1totta).
|
| Előzmény: [1652] Matroz, 2012-02-12 11:31:06 |
|
|
| [1672] jenei.attila | 2012-02-19 23:08:24 |
 Azt hiszem félre értetted, vagy én nem fogalmaztam elég világosan. Én azt írtam, hogy az alfa szögű forgásszimmetriából csak akkor következik a középpontos szimmetria, ha igaz az a feltétel amit írtam. Tehát ha csak annyit tudunk, hogy az alakzatnak van egy alfa szögű forgásszimmetriája, abból csak a mondott feltétel mellet következik a középpontos szimmetria. Te fordítva értelmezted: abból, hogy az alakzat középpontosan szimmetrikus, nyilván nem következik hogy csak a feltételnek megfelelő egyéb alfa szögű forgásszimetriája van csak (vagy ami ugyanez: ha létezik a feltételnek nem megfelelő forgásszimmetria akkor nem igaz az, hogy nem lehet középpontosan szimmetrikus), és ezt nem is állítottam. A körlap nyilván középpontosan szimmetrikus, de nem is csak a feltételnek megfelelő egyéb forgásszimmetriája van. Továbbra is fenntartom, hogy pl. a 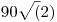 fok forgásszimmetriából nem következik a középpontos szimmetria, de létezik olyan alakzat, aminek mindkét szimmetriája megvan (pl. a körlap). Remélem így már érthető. fok forgásszimmetriából nem következik a középpontos szimmetria, de létezik olyan alakzat, aminek mindkét szimmetriája megvan (pl. a körlap). Remélem így már érthető.
|
| Előzmény: [1671] Róbert Gida, 2012-02-19 22:17:31 |
|
| [1673] jenei.attila | 2012-02-20 09:03:20 |
 Lehet, hogy igazad van, és nem kell bevetni a fixpontokat. Három nem egy ponton átmenő egyenesre történő egymás utáni tükrözés egy csúsztatva tükrözés. Ha kiválasztjuk az alakzat egy pontját és erre alkalmazzuk többször a csúsztatva tükrözést (az eredmény szintén az alakzat pontja kell hogy legyen), akkor az eredetitől egyre távolodó pontokat kapunk, ami ellentmond annak, hogy az alakzat korlátos. Elképzelhető, hogy létezik olyan korlátos alakzat (pl. nyílt körlemez?)amelyre nem alkalmazható a Brouwer tétel (persze ettől még lehetséges, hogy bármely egybevágóságának van fixpontja), viszont igaz rá az eredeti állítás.
|
| Előzmény: [1674] Fálesz Mihály, 2012-02-19 14:04:27 |
|
| [1675] Fálesz Mihály | 2012-02-20 09:45:52 |
 Szia Attila,
Egy egybevágóság fixpontjainak keresésére a Brouwer-tételt kicsit nagy ágyúnak éreztem, ezért kotyogtam bele. (Közben elolvastam alaposabban, amit írtál. :-) )
Ha a Brouwer-tétellel akarjuk az állítást lebombázni, akkor ki kell találnunk egy konvex (esetleg csak a körlemezzel homeomorf), kompakt, és nem üres halmazt, amit az illető egybevágóság önmagába képez. Ez a halmaz lehet például az L konvex burkának lezártja, mert ez az operáció felcserélhető az egybevágóságokkal.
A csúsztatva tükrözést én kétszer hajtanám végre, hogy egy sima eltolás legyen belőle. (Bármelyik megoldásról is legyen szó, meg kell dolgozni azért, hogy véletlenül ne a nullvektorral toljunk el.)
Üdv.
F.M.
|
| Előzmény: [1673] jenei.attila, 2012-02-20 09:03:20 |
|
| [1676] jenei.attila | 2012-02-20 11:13:05 |
 Igazad lehet. Hirtelen ez jutott eszembe, de valóban egyszerűbb és talán általánosabb a csúsztatva tükrözésekkel operálni. A lényeg az, hogy a három nem egy ponton átmenő tengelyre való egymás utáni tükrözések által meghatározott csúsztatva tükrözést páros sokszor alkalmazva egy kiválasztott pontra, a kép pontok mindig egy adott (jó esetben nem nullvektorú) eltolással kerülnek arrébb. Ezek a pontok szintén az alakzat pontjai, ami ellentmond annak, hogy az alakzat korlátos. Szerintem ez lesz a jó megoldás. Most már viszont érdekes kérdés, hogy vajon van-e olyan (korlátos) alakzat, amelyre nem alkalmazható a Brouwer tétel, és létezik fixpont mentes egybevágósága. Vagy az egybevágóságnak mindig van fixpontja, ha az alakzat korlátos? A Brouwer tételhez talán nem kell a konvexitás, elég lehet a zárt körlemezzel való homeomorfia, vagy rosszul gondolom?
|
| Előzmény: [1675] Fálesz Mihály, 2012-02-20 09:45:52 |
|
| [1677] jenei.attila | 2012-02-20 11:38:14 |
 Az "érdekes kérdést" tekintsétek semmisnek, mert butaság. Egybevágóságnak az alakzatot önmagába vivő egybevágósági transzformációt nevezünk, amik definíció szerint tükrözés forgatás, eltolás és csúsztatva tükrözés lehetnek. Korlátos alakzatra csak a tükrözés és a forgatás jön szóba, amiknek van fixpontjuk. Egy korlátos alakzatnak csak egy forgásszimmetria középpontja lehet (viszont több különböző szögű forgásszimmetriája lehet ugyanazon pont körül), és az összes szimmetria tengely ezen a ponton halad át (vagy csak egy tengelyes szimmetriája van). Ez igaz?
|
| Előzmény: [1676] jenei.attila, 2012-02-20 11:13:05 |
|
| [1685] Moderátor | 2012-03-06 15:43:09 |
 Jhony több hozzászólását és az ezekre érkezett válaszokat töröltem.
|
|
|
|
| [1688] Zine | 2012-03-13 21:38:16 |
 Nem szeretnék megoldást kapni, csak ötletet szeretnék kérni, hogyan lehetne belátni a következőt:
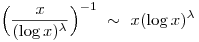
ahol a baloldal a -1-edik hatvány az inverzfüggvényt jelöli. Egy tétel felhasználásával ki tudom hozni, azonban magát a tételt nem teljesen értem, így ettől különböző megoldást szeretnék találni. Előre is köszönöm!
|
|
| [1689] Lóczi Lajos | 2012-03-14 09:31:59 |
 Először is pontosítanod kell a feladatot.
Pl. x a változó? Valós?
 egy paraméter? Valós? Pozitív? 1-nél nagyobb? egy paraméter? Valós? Pozitív? 1-nél nagyobb?
Az aszimptotikus egyenlőséget hol érted? Ha x  ? (Különben a függvény nem is invertálható mindenhol.) ? (Különben a függvény nem is invertálható mindenhol.)
Milyen tételre hivatkoznak?
Próbáld az aszimptotikus egyenlőség két oldalán szereplő kifejezések hányadosának limeszét vizsgálni úgy, hogy "új változót" vezetsz be és így az inverzfüggvény kiküszöbölhető.
|
| Előzmény: [1688] Zine, 2012-03-13 21:38:16 |
|
| [1690] TLevi | 2012-03-14 13:28:54 |
 Sziasztok!
Segitseget szeretnek egy egyenlet megoldasahoz! Az egyenletet mellekelem "*.jpg" formatumban. Nem tudom, hogyan kell kifejeznem a "lambdat" a tobbi ertek fuggvenyeben. (csak a lambda ismeretlen) Elore is koszonom a segitseget!
Udv, TLevi
|
 |
|
| [1691] TLevi | 2012-03-14 13:30:41 |
 Sziasztok!...variacio egy temara:
Segitseget szeretnek egy egyenlet megoldasahoz! Az egyenletet mellekelem "*.jpg" formatumban. Nem tudom, hogyan kell kifejeznem a "lambdat" a tobbi ertek fuggvenyeben. (csak a lambda ismeretlen) Elore is koszonom a segitseget!
|
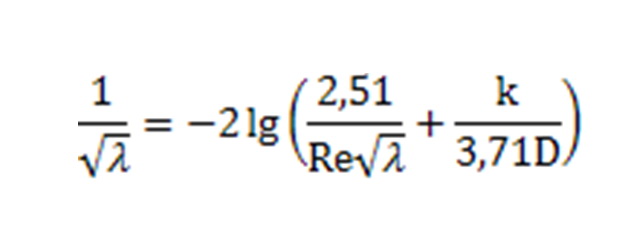 |
|
|
| [1693] TLevi | 2012-03-14 14:53:29 |
 ...A Re - t keplettel kellett kiszamitani...hat Reynolds szam, de valtoztathato mas parameterek fuggvenyeben. A "lambda" is valtoztathato egyutthato. (linearis terheles-vesztessegi egutthato)...(remelem jo a forditas)
|
| Előzmény: [1692] Lóczi Lajos, 2012-03-14 14:43:54 |
|
| [1694] Lóczi Lajos | 2012-03-14 18:43:43 |
 Általában az ilyen transzcendens egyenletekből véges sok elemi függvénnyel nem lehet kifejezni a változókat. A te példád is ilyen. Tulajdonképpen csak a numerikus megoldás jön szóba.
Ha mégis kell valamilyen "formula", akkor  kifejezhető pl. a Lambert-féle W-függvénnyel, lásd az Examples részt. Praktikusan persze ez nem jelent sok segítséget. kifejezhető pl. a Lambert-féle W-függvénnyel, lásd az Examples részt. Praktikusan persze ez nem jelent sok segítséget.
|
| Előzmény: [1693] TLevi, 2012-03-14 14:53:29 |
|
| [1695] TLevi | 2012-03-15 08:06:04 |
 Kosz a segitseget!
De... sajnos a matek nem az eros oldalam Lehetseges, hogy ha adok ertekeket, akkor kaphatnek egy erteket a labdara?
ha igen, akkor:
D=0,051545455 [m] k=0,07 [cm] Re=5885548.364 (valtoztatdato kellene legyen de ebben az esetben ennyi)
Tehat, ha ezekkel sikerulne egy lambda erteket kapni, az jo lenne (erre az esetre...de az meg jobb lenne, ha a lamdat a D es a Re fuggvenyeben lehetne valtoztatni)
Elore is kosz' a segitseget!
Tisztelettel TLevi
|
| Előzmény: [1694] Lóczi Lajos, 2012-03-14 18:43:43 |
|
| [1696] Kemény Legény | 2012-03-15 08:52:18 |
 Nem használhatsz valamilyen matematikai segédprogramot, ami numerikusan megoldja az egyenletet? Például Maple, Mathematica, Matlab,... mind rendelkezik beépített numerikus egyenletmegoldóval.
Azt mellesleg tudod, hogy az 1690-es és 1691-es képleteid nem ekvivalensek? (egy negatív előjel nem stimmel).
Az 1691-es megoldása numerikusan:   1.3123. Ezt online is megkaphatod a WolframAlpha segítségével. 1.3123. Ezt online is megkaphatod a WolframAlpha segítségével.
|
| Előzmény: [1695] TLevi, 2012-03-15 08:06:04 |
|
|
|
| [1699] TLevi | 2012-03-16 10:58:19 |
 szia!
Hogy miert van ket mertekegyseg az egyenletben? ezek az ertekek igy vannak megadva mertekegysegekkel, de ahogy ertem, a lambdanak nincs mertekegysege.
|
| Előzmény: [1697] jonas, 2012-03-15 09:12:48 |
|
| [1700] TLevi | 2012-03-16 11:07:46 |
 Igen, az lg tízes alapú logaritmust jelent. Igen, a 2,51 és 3,71 konstansokat csak három jegy pontosan ismerem. Tovabb folytatnam ... a lambdat meg mindig nem sikerul kifejeznem (kello mennyisegi es milyensegu matematikai ismereteim hianya miatt). Tehat, ha kapnek egy egyszeru megoldast erre az egyenletre (pl. igy: lambda egyenlo..... - tehat nem "1/gyok lambda egyenlo.....), az megint nagyon jo lenne ha ezt parametrikusan tudnam valtoztatni a tobbi valtozo (D es Re) fuggvenyeben (pl. Excelbe beirt keplettel). Megegyszer: sajnos a matek nem az erossegem!
Tisztelettel TLevi
|
| Előzmény: [1698] jonas, 2012-03-15 09:17:19 |
|
| [1701] Lóczi Lajos | 2012-03-16 13:23:44 |
 A válasz már kétszer elhangzott korábban a kérdésedre: nincs "egyszerű megoldás erre az egyenletre", csak olyan, amelyik speciális függvényt tartalmaz. (És ez nem azon múlik, hogy valakinek milyen "mennyiségű és milyenségű" matematikai ismerete van -- az egyenlet fajtája ilyen.)
Az a program (pl. Excel), amelyet a konkrét számolásra szeretnél használni, tud a (korábban már említett) Lambert-féle W-függvénnyel dolgozni? Ha igen, felírok egy formulát, amelyet a D és Re paraméterekkel tudsz manipulálni és az egyenlet megoldását adja  -ra. -ra.
|
| Előzmény: [1700] TLevi, 2012-03-16 11:07:46 |
|
| [1702] jonas | 2012-03-16 20:47:33 |
 Azért még egy kérdésem van. A [1691] vagy a [1690] egyenletet kell nézni? Esetleg külön-külön mindkettő érdekel? Kemény Legény az előbb észrevette, hogy ezek különböznek.
|
| Előzmény: [1700] TLevi, 2012-03-16 11:07:46 |
|
|
| [1704] SmallPotato | 2012-03-16 21:21:14 |
 Gyanús volt a képlet, utánakerestem (ha már a közzétevő titkot csinál belőle).
A Colebrook–White-képletről van szó; a D az egyenértékű csőátmérő (teljes keresztmetszetben kitöltött cső esetében a valódi belső átmérő); Re a Reynolds-szám, amely a viszkozitás, a csőátmérő és az áramlási sebesség függvényében több nagyságrendet fog át.
A legszebb, hogy a szócikkben szerepel is, hogy az egyenlőséget a  csősúrlódási tényező iteratív kiszámítására használják. csősúrlódási tényező iteratív kiszámítására használják.
|
| Előzmény: [1703] jonas, 2012-03-16 20:50:24 |
|
|
| [1706] Sirpi | 2012-03-17 23:21:36 |
 Találtam egy új problémát, nem tudom, mennyire van kivesézve.
Legyen a1,a2,... egy végtelenbe tartó egész számsorozat, és számjegyátlagának liminf-je legyen A, limsup-ja B.
Ekkor nyilván 0 A A B B 9, de nevezetes sorozatoknál tudunk ennél többet is mondani? 9, de nevezetes sorozatoknál tudunk ennél többet is mondani?
Például ha an=n2, akkor A = 0, és B 4,5, de B-re van jobb? Az 1, 2, stb. jegyű számokra a maximális számjegyátlag így alakul (optimum, számjegyátlaga): 4,5, de B-re van jobb? Az 1, 2, stb. jegyű számokra a maximális számjegyátlag így alakul (optimum, számjegyátlaga):
9 9.000000
49 6.500000
289 6.333333
6889 7.750000
97969 8.000000
698896 7.666667
9696996 7.714286
79869969 7.875000
876988996 7.777778
És ha an=2n, arra tud valaki bármi építő jellegűt?
|
|
| [1707] Kemény Legény | 2012-03-18 20:27:15 |
 Nem biztos, hogy közelebb visz a megoldáshoz - már ha egyáltalán megválasztható a kérdés - de négyzetszámok esetén B 6, ugyanis 6, ugyanis
533...32=2844...4088...89,
ahol n db 3-as követi az 5-öst, illetve n-1 db 4-es és 8-as van egymás mellett az eredményben. Talán szerencsésebb próbálkozással ennél jobb is található, idő hiányában nem vizsgáltam tovább, amint 4.5-nél jobbat találtam, megálltam.
|
| Előzmény: [1706] Sirpi, 2012-03-17 23:21:36 |
|
| [1708] Kemény Legény | 2012-03-18 20:35:35 |
 733...32=5377...7288...89
még jobb választás, erre B 7.5 jön ki. Ez már közel lehet a megoldáshoz, ugyanis az OEIS adatbázisban A069665 néven további elemei is meg vannak adva a sorozatnak, amik kb. ilyen átlagot produkálnak (de nincs semmi dokumentum a további referenciák között). 7.5 jön ki. Ez már közel lehet a megoldáshoz, ugyanis az OEIS adatbázisban A069665 néven további elemei is meg vannak adva a sorozatnak, amik kb. ilyen átlagot produkálnak (de nincs semmi dokumentum a további referenciák között).
|
| Előzmény: [1707] Kemény Legény, 2012-03-18 20:27:15 |
|
|
|
|
|
|
|
| [1715] Hölder | 2012-03-20 10:31:26 |
 Sziasztok!
Van egy feladat, amire próbáltam elemi (differenciálás nélküli) megoldást is keresni, de nem találtam. Ha nektek van megoldásotok, amiben pl. közepek, Jensen-egyenlőtlenség szerepel, stb., tehát elemibb eszközök, akkor azt ossza meg velem is.
A feladat: keressük meg a 2 a sin x-ediken +2 a cos x-ediken függvény maximumát!
megjegyzés: a minimumra van elemi megoldás (közepek), a maximumot pedig "nyilván" 45 foknál veszi fel.Elnézést, hogy nem szépen írtam be a feladatot.
|
|
|
|
| [1718] Lóczi Lajos | 2012-03-21 21:33:58 |
 Érdekes, hogy deriválással könnyen meghatározható az 5 /4-nél lévő minimum (csak egy Bolzano-tétel -- ez az a szélsőérték, ami neked is kijött már elemi módszerekkel), de a /4-nél lévő minimum (csak egy Bolzano-tétel -- ez az a szélsőérték, ami neked is kijött már elemi módszerekkel), de a  /4-nél lévő maximummal meg kellett egy kicsit küzdenem. /4-nél lévő maximummal meg kellett egy kicsit küzdenem.
Vagyis a kérdésem az, hogy hogyan lehetne minél egyszerűbben belátni, hogy a
tg(x)=2sin (x)-cos (x)
egyenletnek a [0,2 ] intervallumban pontosan 2 gyöke van? (Az x ] intervallumban pontosan 2 gyöke van? (Az x ( ( /2,2 /2,2 ] intervallum tehát könnyű, ami szerintem nem látszik egyszerűen, az az x ] intervallum tehát könnyű, ami szerintem nem látszik egyszerűen, az az x [0, [0, /2) tartomány.) /2) tartomány.)
|
| Előzmény: [1717] Hölder, 2012-03-20 20:46:47 |
|
| [1719] Hölder | 2012-03-22 12:21:33 |
 Én egy kicsit máshogy közelítettem meg a dolgot, bár el kell ismerjem, először én is úgy próbáltam, mint te. Szóval 2 a sinx-ediken /(sinx) = 2 a cos x-ediken /cosx (nyilván sinx= 0 és cosx=0 nem jöhet szóba, ezért nyugodtan oszthatunk vele).És itt érdemes bevezetni a g(x) =2 az x-ediken /x függvényt, ezt vizsgálni a [-1,1]-ban, hiszen az argumentumok sinx és cos x. Ha megnézed, ennek 1/ln 2-ben lesz szélsőértéke, ami 1-nél nagyobb, tehát előtte monoton a függvény, amiből adódik, hogy sinx=cosx, azaz tgx=1, innen jönnek a szélsőértékek, de ez sajnos nem elemi megoldás, és valahogy úgy érzem valami nagyon trükkös elemi megoldás is van, csak én nem találtam meg. Amúgy hogy lehet itt matematikai dolgokat beírni?
|
| Előzmény: [1718] Lóczi Lajos, 2012-03-21 21:33:58 |
|
|
| [1721] Lóczi Lajos | 2012-03-22 22:56:02 |
 Valamilyen a>1 esetén tekintsük az asin (x)+acos (x) függvényt a [0,2 ) intervallumon. Ha pl. a=2, akkor f-nek pontosan 2 szélsőértékhelye van. ) intervallumon. Ha pl. a=2, akkor f-nek pontosan 2 szélsőértékhelye van.
Van olyan a>2 érték, amikor ez nem igaz? Mi az "első" ilyen kritikus érték?
|
|
| [1722] spongya | 2012-03-22 23:24:12 |
 "Ha sikerülne elemi eszközökkel belátni, hogy 2sin(x) alulról konkáv, ..."
Nekem + az jött ki, hogy ![[0;\frac13]](keplet.cgi?k=81A3E1FD6E32E2F2) -ban 2sin(x) alulról konvex. Sőt, a konvexitási tartomány jobbra még kicsit szélesíthető is. Vagy rosszul látom? -ban 2sin(x) alulról konvex. Sőt, a konvexitási tartomány jobbra még kicsit szélesíthető is. Vagy rosszul látom?
|
| Előzmény: [1720] HoA, 2012-03-22 20:05:27 |
|
|
|
| [1725] Fálesz Mihály | 2012-03-23 16:32:36 |
 Én inkább a 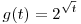 függvényt vizsgálnám. A második derivált mutatja, hogy g a függvényt vizsgálnám. A második derivált mutatja, hogy g a ![[0,1]\subset\Big[0,\frac1{(\ln2)^2}\Big]](keplet.cgi?k=6C89DEA734520B16) intervallumban konkáv: intervallumban konkáv:
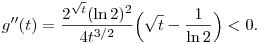
Ezért hát a Jensen-egyenlőtlenséget a g függvényre és az sin2x, cos2x pontokra felírva,
2sin x+2cos x 2|sin x|+2|cos x|=g(sin2x)+g(cos2x) 2|sin x|+2|cos x|=g(sin2x)+g(cos2x)
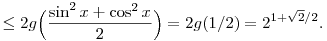
|
| Előzmény: [1722] spongya, 2012-03-22 23:24:12 |
|
|









 egy paraméter? Valós? Pozitív? 1-nél nagyobb?
egy paraméter? Valós? Pozitív? 1-nél nagyobb? 
 ? (Különben a függvény nem is invertálható mindenhol.)
? (Különben a függvény nem is invertálható mindenhol.) 
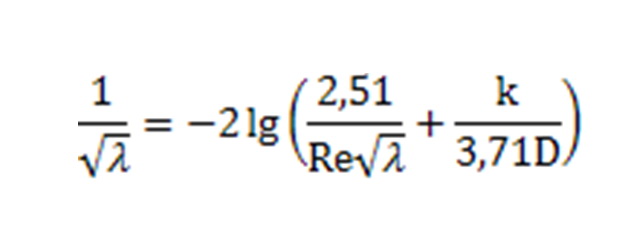
 1.3123. Ezt
1.3123. Ezt 


 A
A 4,5, de B-re van jobb? Az 1, 2, stb. jegyű számokra a maximális számjegyátlag így alakul (optimum, számjegyátlaga):
4,5, de B-re van jobb? Az 1, 2, stb. jegyű számokra a maximális számjegyátlag így alakul (optimum, számjegyátlaga):  /4-nél lévő minimum (csak egy Bolzano-tétel -- ez az a szélsőérték, ami neked is kijött már elemi módszerekkel), de a
/4-nél lévő minimum (csak egy Bolzano-tétel -- ez az a szélsőérték, ami neked is kijött már elemi módszerekkel), de a  (
(