|
| [303] epsilon | 2008-03-01 21:28:00 |
 Köszi Lajos! 1) A 297 feladat esetén azért gondoltam a deriváltra, mert egyik értelmezése az alulról konvexnek az, hogy a [0,1] intervallumon a függvény bármely pontjában húzott érintő a függvény ábra alatt van. és a derivált mértani jelentése alapján arra is gondoltam.Az a=0 és a=1 valóban az, de a helyes válasz az, hogy PONTOSAN 2 megoldás, tehát maradna, miért nincs más "a" érték? 2)A 298 esetén nem értem a kérdve kifejtett "válaszod", szóval ott a megoldókulcs alapján az (E) a helyes, de ...mint írtam, Én ki tudok hozni eredményeket a nem helyesek kötül, és...nem látom a tévedést, tehát érdekelne: MIÉRT az (E) válasz a helyes? Vagyis mi a helyzet azzal a limesszel, mennyi, vagy nem létezik? 3) A 299 esetén Én néztem el a válasznak megjelölt betűt! Üdv: epsilon
|
| Előzmény: [302] Lóczi Lajos, 2008-03-01 19:30:01 |
|
| [304] Lóczi Lajos | 2008-03-01 23:49:03 |
 Az A-E-s tesztben ugye csak 1 helyes megoldást karikázhatunk be? (Számolás nélkül) azt gondoltam, hogy az a2, a3 kezdőértékek alkalmas megválasztásával többféle limesz is kihozható, tehát a végeredmény nem egyértelmű, ezért E. Te milyen lehetséges értékekek kapsz?
|
| Előzmény: [303] epsilon, 2008-03-01 21:28:00 |
|
| [305] Lóczi Lajos | 2008-03-02 00:45:31 |
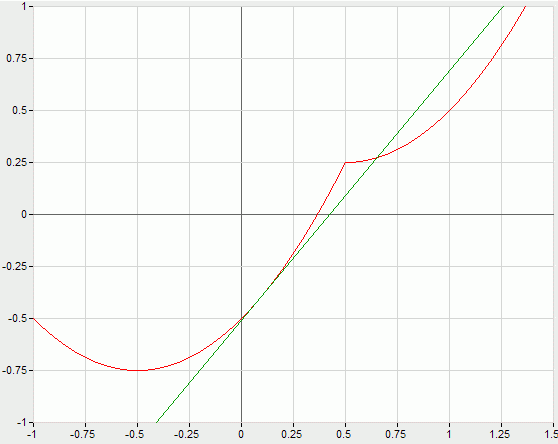
 Ha a (0,1) a nyílt intervallumban van, akkor f nem deriválható x=a-ban, mert a két félérintő különböző szöget zár be: a balérintő meredeksége 2a+1, míg a jobbérintőé 2a-1. A balérintő mindig pozitív meredekségű és meredekebb, mint a jobbérintő. A függvény tehát nem lehet konvex. (0,1) a nyílt intervallumban van, akkor f nem deriválható x=a-ban, mert a két félérintő különböző szöget zár be: a balérintő meredeksége 2a+1, míg a jobbérintőé 2a-1. A balérintő mindig pozitív meredekségű és meredekebb, mint a jobbérintő. A függvény tehát nem lehet konvex.
|
| Előzmény: [303] epsilon, 2008-03-01 21:28:00 |
|
|
| [307] epsilon | 2008-03-02 06:48:08 |
 Kedves Lajos! Teljesen egyetértek a 305-ös észrevételeddel, éppen a 2a-1=2a+1 absurdum jött ki (amikor a deriválhatóságot említettem), és ezek szerint akkor mégis miért állhat a jelzett válasz, hogy pont 2 a érték van amelyre konvex? Természetesen MINDEN feladat esetén PONTOSAN 1 válasz helyes, és az biztosan helyes. A 304-es észrevételedre és eredményeimre visszatérek, megírom a saját számolásaimat, mert túl szép, és érdekesnek tűnik az egész feladat. Kösz, hogy foglalkoztál vele! Üdv: epsilon
|
| Előzmény: [305] Lóczi Lajos, 2008-03-02 00:45:31 |
|
| [308] epsilon | 2008-03-02 07:38:15 |
 Helló! Mivel csak MathType-ban dolgozok, és a képlopóval a képek mérete meghaladja a megengedettet, ezért részletekben írok. A legtöbb valószínűséggel a határértéknek az e értéket tulasdonítanám, noha a következő bizonyításban a "részleges határértékre térés" vitatott lehet, ami miatt az eredmény is.
|
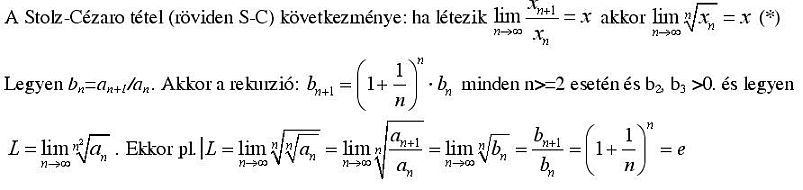 |
|
| [309] epsilon | 2008-03-02 07:48:39 |
 Ugyancsak ez jön ki a következő képpen, ha S-C és a (*) együttes alkalmazását végzem, de itt a "részleges határértékre térés" szerintem már nem mondható (?)
|
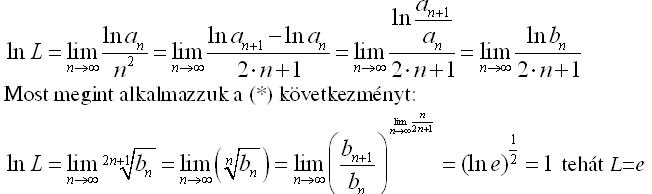 |
|
| [310] epsilon | 2008-03-02 07:53:16 |
 Megint más, noha látható, hogy a b(n) sorozat növekvő, és limesze nem lehet 0:
|
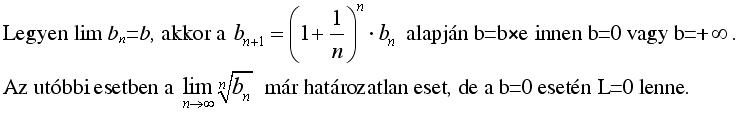 |
|
| [311] epsilon | 2008-03-02 07:59:00 |
 A 304-es hsz kapcsán: ha egy limeszt többféle képpen helyesen számolunk ki, akkor nem lehet különböző eredménye, de nagyon negéz eldönteni, hogy most a többféle eredmény alapján azért a "más válasz" a helyes, mert többféle eremény jött ki helyesen? vagy ??? Azzal egyetértek, hogy a kezdetértékek befolyásolják a limeszt, éppen ezért az eredeti rekurziót logaritmáltam, így egy 2-ik rendű nemhomogén rekurzió jött létre, a homogén egyenletnek dupla gyöke van, valóban a kezdetértékek bennemaradnak a szokásos 2 paraméter meghatározásában, de egyenlőre még az ebből adódó limesz kiszámolásával, nem jutottam dűlőre. Más ötletem az volt, hogy a b(n)-ben levő rekurzióban, lévén, hogy egymásutáni tagokról van szó (a két oldalon), összeszorozva, az a(n) sorozat általános tagját megkaptam, de az L kiszámolásával elakadtam :-( Szóval eléggé ingoványos talajokra is jutottam. üdv: epsilon
|
|
| [312] epsilon | 2008-03-02 08:52:36 |
 Keves Lajos! Más irányból közelítettem meg a feladatot, és az kiderült, hogy a két kezdetérték nem befolyásolja a limeszt:
|
 |
|
| [313] epsilon | 2008-03-02 08:53:27 |
 A p>=2 helyett k>=2 kell ( a képben már nem javítottam ki)
|
|
| [314] epsilon | 2008-03-02 09:15:39 |
 Vajon ez már jó megoldás lenne:
|
 |
|
| [315] nadorp | 2008-03-03 11:21:29 |
 Ne haragudj, de szerintem már a kiindulási új rekurzió is rossz. Nem értem, hogy jött ki a bk+1=ek.bk
Különben, ha 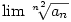 létezik, akkor az csak 1 lehet, ui. a rekurzióból létezik, akkor az csak 1 lehet, ui. a rekurzióból

Tehát 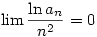
|
| Előzmény: [312] epsilon, 2008-03-02 08:52:36 |
|
| [316] epsilon | 2008-03-03 16:23:32 |
 Helló nadorp! Ne haragudj, de többvalami elkerülte a figyelmedet: 1) Lennebb beidézem a kiinduló feladatot, és ott meglátod miről van szó! 2) A rekurzióban teljesen mindegy, hogy n-et vagy k-t írunk, nem de? 3) Az aránypárok tulajdonságát használtam, és az a(n+2) alá hoztam az egyik a(n+1)-et, és a jobboldalon a nevezőbe vittem az ottmaradt a(n+1) alá az a(n)-et. 4) Ha tehát a(n+1)/a(n) a jobboldalon b(n)-el lett jelölve, akkor a baloldalon a(n+2)/a(n+1) egyértelműen b(n+1). Aztán a teljes rekurziót átírtam n helyett k-ra, és az (1+1/k)-nek az k-adik hatványát e(k)-val jelöltem, és a kapot, általad beidézett rekurzió szerintem teljesen igaz. 5) Az általad kihozott 0 erdménysajnos 101 százalékban HIBÁS, a feladatnál jeleztem, hogy melyik a helyes válasz, a könyvet majdnem mind ilyen feladatokkal állították össze, sok minden látszatra úgy tűnik, hogy jó, de a helyes válasz nem az. Ismételem, a helyes válasz az (E) erre mérget lehet venni, íme mégegyszer a feladat, és kösz, hogy foglalkozol vele. Még van egy pár tucat ilyen, feladat, ami látszatra másnak tűnik, mint ami a helyes válasz! Üdv: epsilon.
|
 |
|
| [317] Lóczi Lajos | 2008-03-03 16:41:31 |
 "és ezek szerint akkor mégis miért állhat a jelzett válasz, hogy pont 2 a érték van amelyre konvex?"
Ha a=0 vagy a=1, akkor a töréspont a [0,1] intervallum végpontja, és a törésponttól balra és jobbra, külön-külön, a függvény eleve konvex: a konvexitással probléma csak akkor van, amikor a töréspont a [0,1] intervallum belsejébe kerül.
|
| Előzmény: [307] epsilon, 2008-03-02 06:48:08 |
|
| [318] epsilon | 2008-03-03 16:47:46 |
 Tehát mégegyszer: a lehetséges válaszokból (valami hibás gondolatmenet folytán?) kihozható a limesz értékének a 0, az 1 az e akármylike, de egyik sem jó (az e és 0-át mutattam, hogy kijöhetne de nem jó válasz, az 1-et Te hoztad ki, még nem látom miért, az sem a jó válasz). Az eredmény végtelen sem lehet, tehát a "más válasz" alapján a felsoroltakon kívül van a helyes eredmény.
|
|
| [319] Lóczi Lajos | 2008-03-03 17:02:01 |
 "aránypárok tulajdonságát használtam, és az a(n+2) alá hoztam az egyik a(n+1)-et, és a jobboldalon a nevezőbe vittem az ottmaradt a(n+1) alá az a(n)-et."
Összesen csak 1 db an+1 van, ha azt átviszed a bal oldalra, a jobb oldalon nem marad már meg!
|
| Előzmény: [316] epsilon, 2008-03-03 16:23:32 |
|
|
| [321] epsilon | 2008-03-03 17:56:23 |
 Huh a rézangyalát! Elnézést kérek Mindenkitől! Annyira bele vagyok merülve ebbe meg az ilyen típusú csapdás feladatokba, hogy egy 2-es hatványkitevőt elhagytam, amire egyébként a megoldásaimat is leírtam, tehát elnézéseteket kérve a rekurzió HELYESEN:
|
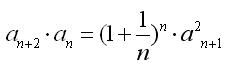 |
|
|
| [323] epsilon | 2008-03-03 18:26:27 |
 Kedves Lajos! Örvendek, hogy megint jelentkeztél, mert továbbra is érdekelne a 297-es feladat tisztázása (ezúttal nem írtam el), vagyis, hogy miért edták arra azt a választ, hogy PONTOSAN 2 olyan "a" érték van amelyre az konvex lenne. Mint láttuk, az x=a-ban nem deriválható, viszont Te meg írod a 302-ben, hogy az a=0 és a=1 esetben konvex, bocs de Én nem látom miért, mert ebben a 2 esetben is fennáll a már említett 2a-1=2a+1 absurdum, ami az a pontban való deriválhatóság származtat.(vagyis nem húzható az érintő, és ebben a pontban nem érvényes a konvexitás jelzett értelmezése!?) Üdv: epsilon
|
|
| [324] epsilon | 2008-03-03 18:51:57 |
 Kedves Lajos! Az a=0 és a=1 értékek esetén a 2 tagra alkalmazott Jensen-féle egyenlőtlenség valóban megadja az f konvexitását, kösz a hozzászólásod ahol írtad! Most már csak az a furcsa, mint írtam, hogy ezekben az esetekben is fennáll az, hogy az x=0 ill. x=1 esetekben nem teljesül a 2a-1=2a+1, vagyis a deriváltal=érintőmeghúzhatósággal való gond továbbra is homályosít? Mi a valódi helyzet, miért van ez a látszólagos ellentmondás? Mert azzak, hogy e 2 pontban konvex, még nem zárja ki, hogy más ban ne lenne az!? Üdv: epsilon
|
|
| [325] nadorp | 2008-03-03 21:56:02 |
 Az 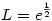 szerintem is jó. Én így számoltam: szerintem is jó. Én így számoltam:
Könnyen látszik, hogy 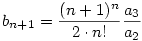 , ahonnan - felhasználva a Stirling formulát - , ahonnan - felhasználva a Stirling formulát -
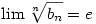 , azaz , azaz
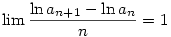 . .
Tetszőleges  >0-hoz létezik N, hogy >0-hoz létezik N, hogy
(1- )N+ln aN<ln aN+1<(1+ )N+ln aN<ln aN+1<(1+ )N+ln aN )N+ln aN
(1- )(N+N+1)+ln aN<ln aN+2<(1+ )(N+N+1)+ln aN<ln aN+2<(1+ )(N+N+1)+ln aN )(N+N+1)+ln aN
...
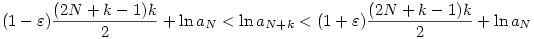 teljesül minden k-ra, azaz teljesül minden k-ra, azaz
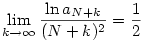
|
| Előzmény: [314] epsilon, 2008-03-02 09:15:39 |
|
|
| [327] Lóczi Lajos | 2008-03-03 23:38:57 |
 A törés természetesen fennáll, de vedd figyelembe, hogy az f függvényed értelmezési tartománya csak a [0,1] intervallum volt, tehát érdektelen számunkra, mi és hogy törik azon kívül.
|
| Előzmény: [324] epsilon, 2008-03-03 18:51:57 |
|
|
| [329] epsilon | 2008-03-04 06:24:17 |
 Köszi nadorp a megerősítést! Én csak azon csodálkozom, hogy lehet ilyen feladatokat tesztfeladatoknak adni feleletválasztósnak, hiszen a többi eredmény csak kelepce volt, végül is meg kell oldani, és nincs semmi ami a feleletválasztóshoz kapcsolná.(sem logikai kizárások, stb.)
|
|
| [330] epsilon | 2008-03-04 06:30:32 |
 Kedves Lajos és Cauchy! Kösz a magyarázatokat, de még mindig nem világos számomra az pl, hogy mondjuk az a=1/2 értékre miért nem konvex (mert ez ugye nincs a [0,1]-en kívük, és mégsem konvex?! (A derivált esetén a törést megértettem, hiszen mondjuk lehet akár szögpont, visszatérőpont, stb. ahol a két szélső derivált nem egyenlő, a pontban húzott "félérintők" így is a grafikus ábra alatt maradnak.)
|
|
|
|
|
|
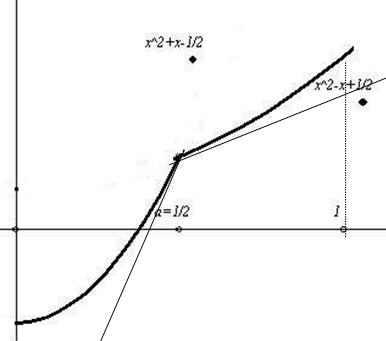
| [335] epsilon | 2008-03-04 14:21:49 |
 Helló nadorp! gondolom, hogy ezzel nem lehetne belátni, hogy a (0,1) intervallumon nem lenne konvex (csak egy értéket mondtam), és az ábrádon megpróbáltam csak a függvényt meghagyni, és az 1/2-ben van bal illetve jobboldali "alsó érintő" és miért ne lenne konvex az a függvény, amt így látunk?
|
 |
| Előzmény: [331] nadorp, 2008-03-04 09:43:27 |
|
|
|
| [338] sakkmath | 2008-03-04 15:48:23 |
 Egyetértőleg csatlakozom az előttem szólóhoz. A 297. feladat szövege nem szól az f függvény [0;1]-beli differenciálhatóságáról, ezért a kovexitás érintős definícióját ne használjuk. A konvexitás kérdésében - tankönyv híján - vegyük a WIKIPÉDIA másik definícióját:
Az f: I  R intervallumon értelmezett valós változójú függvény konvex, ha a függvénygörbe (bármely, az adott intervallumba eső ÿ(kiegészítés tőlem)) két pontját összekötő húr a függvénygörbe fölött halad ... R intervallumon értelmezett valós változójú függvény konvex, ha a függvénygörbe (bármely, az adott intervallumba eső ÿ(kiegészítés tőlem)) két pontját összekötő húr a függvénygörbe fölött halad ...
|
|
| [339] epsilon | 2008-03-04 17:49:25 |
 OK, köszi mindkettőtöknek! Így már tiszta!
|
|
|
| [341] Lóczi Lajos | 2008-03-04 22:29:48 |
 Még egyszer hadd térjek vissza a problémára egy utólagos elemzés erejéig, más kiindulással és kevésbé explicit érveléssel, a Stirling-re való hivatkozás nélkül.
A hányados- és gyökkritérium témaköréből ismert a következő egyenlőtlenséglánc:
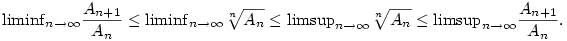
(Ez a lánc egyébként azt mondja, hogy a gyökkritérium erősebb a hányadoskritériumnál.)
A megadott rekurziót az en=(1+1/n)n és 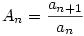 jelölésekkel így írhatjuk át: jelölésekkel így írhatjuk át:
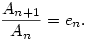
Mivel itt a jobb oldal liminf-je és limsup-ja egyaránt e, a fentiekből rögtön adódik, hogy létezik
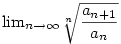
és e-vel egyenlő. Innen a továbbhaladás már hasonló (de logaritmálás nélkül is megy a dolog persze), a limesz definíciójából kiindulva megmutatjuk, hogy létezik
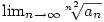
és 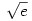 -vel egyenlő. -vel egyenlő.
|
| Előzmény: [325] nadorp, 2008-03-03 21:56:02 |
|
| [342] epsilon | 2008-03-05 06:37:26 |
 Kedves Lajos! Örvendek, hogy megerősíted ezt a megoldási lehetőséget, a 308-as hozzászólásnál Én is ezt próbáltam bemutatni, Én ugyan a Stolz-Cezaro tétel 3. következménbyeként ismerem, ugyanis azzal levezethető, de Cauchy-D'Alambert tételnek forgalmazzák a Sorok elméletében, a lényeg az lenne, hogy: 1) Írtad, hogy "megmutatjuk", hogy a limesz a végén gyök e, 2) Ha jól akartam, a 308-nál ugyanezt végeztem, de a parciális határértékretérés gyanúja állt fenn, ott meg a limesz e-nek jött ki. Van valami kiegészítésed, hogyan is jön ki pontosan a gyök e, (vagyis a "megmutatjuk" hogyanja) meg miért van ellentmondásba az eredmény a 308-cal, mert nagyon tetszik ez a megoldásod, hiszen a teszt középiskolásoknak szól, így nagyágyúval rálőni nem fair, amit mutattam szerintem az is elég hosszadalmas, szerintem ilyesfélén ahogyan írtad egészen plauzíbilis! Üdv: epsilon
|
|
| [343] epsilon | 2008-03-05 06:40:40 |
 Igen érdekes elgondolkodni a konvexitás fogalmának a defieálásán, hiszen mint az érintős meghatározás, mint az, hogy f"(x) ne legyen negatív nem igazán fogadható el ezek szerint a konvexitás értelmezésének, mert a derivált belekeverése nem "fair" tehát legtisztább a húrral defineálni és úgy tanítani, noha sok szakkönyvben nem éppen így teszik.
|
| Előzmény: [340] Lóczi Lajos, 2008-03-04 22:07:31 |
|
| [344] nadorp | 2008-03-05 08:45:21 |
 Én még úgy tanultam, hogy egy függvénygörbe konvex egy [a,b] intervallumon, ha tetszőleges két pontját összekötő szakasz felezőpontja görbe felett (vagy rajta) van.Ha az intervallumon a függvény kétszer deriválható, akkor a második deriváltak nemnegativitása szükséges és elegendő feltétel, de ez már tétel. Esetünkben az eredeti definíció érvényességét tudjuk csak vizsgálni, hiszen a függvény az x=a pontban nem deriválható.
|
| Előzmény: [343] epsilon, 2008-03-05 06:40:40 |
|
| [345] epsilon | 2008-03-05 10:23:25 |
 Valóban, a másodrendű deriváltat Én is csak tételként használom, noha láttam könyvet ahol definició, de mi régen az érintős definiciót tanultuk, és még mindig sok helyen így tanítják, de mint látható, most sem állta a helyét, de a felezőpontos definiciót nem igazán tanítottak, úgyhogy megérte itt erről is hallani ;-)
|
|
|
| [347] Lóczi Lajos | 2008-03-05 12:38:27 |
 Egy "konvexitásdefiníció" annál általánosabb, minél kevesebbet követel meg az f függvényről. Az említett 3 értelmezés közül a legáltalánosabb az, amelyben nincs simasági (azaz deriválhatósági) megkötés: ebben csak a húr szerepel. Ezzel a definícióval igaz, hogy ha f egyszer deriválható, akkor a konvexitás egyenértékű a derivált monoton növekedésével. Továbbá, ha a függvény kétszer deriválható, akkor a konvexitás egyenértékű a második derivált nemnegativitásával.
Ha valaki a konvexitást az első deriválttal akarja definiálni, kevesebb függvényt tudna konvexnek mondani. Hasonlóan, ha a második derivált lenne a definícióban, még tovább szűkülne a "konvex függvény" fogalma.
Mindazonáltal igaz az a tétel, hogy egy -- intervallumon értelmezett és a húros definíció értelmében -- konvex függvény (Lebesgue-) majdnem mindenütt deriválható, sőt, egy megszámlálható halmaz kivételével mindenütt deriválható.
|
| Előzmény: [346] cauchy, 2008-03-05 12:02:50 |
|
| [348] Lóczi Lajos | 2008-03-05 13:38:37 |
 "Ha jól akartam, a 308-nál ugyanezt végeztem, de a parciális határértékretérés gyanúja állt fenn, ott meg a limesz e-nek jött ki."
Általában nem szabad egy részkifejezést a határértékével helyettesíteni, vagy két kifejezést egymással helyetteíteni, mégha a limeszük ugyanaz is, mert akkor fals eredmények jöhetnek ki: ezt tetted a [308]-as végén is, s ezért jött ki rossz eredménynek e a végére.
A fenti manipulációk veszélyességéről rögtön meggyőződsz, ha a hibás

sorra pillantasz, "hiszen 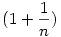 és 1 limesze ugyanaz a végtelenben". és 1 limesze ugyanaz a végtelenben".
|
| Előzmény: [342] epsilon, 2008-03-05 06:37:26 |
|
| [349] Lóczi Lajos | 2008-03-05 13:57:32 |
 "1) Írtad, hogy "megmutatjuk", hogy a limesz a végén gyök e, ... Van valami kiegészítésed, hogyan is jön ki pontosan a gyök e, (vagyis a "megmutatjuk" hogyanja)..."
Ez a gondolat ugyanaz, mint a nadorp által [325]-ben felvázolt (csak logaritmusvétel nélkül): az 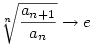 limesz definíciója szerint minden limesz definíciója szerint minden  >0-hoz van olyan N( >0-hoz van olyan N( ), hogy az N-nél nagyobb n-ekre (e- ), hogy az N-nél nagyobb n-ekre (e- )nan<an+1<(e+ )nan<an+1<(e+ )nan. Ebből rekurzívan felírsz egy közrefogást aN+k-ra (k tetszőleges természetes szám), majd e )nan. Ebből rekurzívan felírsz egy közrefogást aN+k-ra (k tetszőleges természetes szám), majd e  kitevőiben elvégzed az összegzést, így egy kitevőiben elvégzed az összegzést, így egy
(e- )valami.aN<aN+k<(e+ )valami.aN<aN+k<(e+ )valamihasonlo.aN )valamihasonlo.aN
alakú egyenlőtlenséghez jutsz. Most k2-edik gyököt vonunk, a lánc bal és középső tagjában liminf-et veszünk, míg a középső és jobb tagjában limsup-ot, majd kihasználjuk, hogy pl. 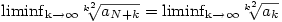 (hiszen N most fix; vagyis a fix indexeltolás nem befolyásolja a liminf/limsup értékét), ebből azt kapjuk, hogy (hiszen N most fix; vagyis a fix indexeltolás nem befolyásolja a liminf/limsup értékét), ebből azt kapjuk, hogy
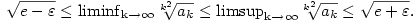
A fenti érvelés viszont minden  >0-ra igaz, emiatt létezik tehát >0-ra igaz, emiatt létezik tehát 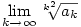 és értéke és értéke 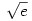 . .
|
| Előzmény: [342] epsilon, 2008-03-05 06:37:26 |
|
| [350] epsilon | 2008-03-05 16:10:49 |
 Nem, éppen azt igazoltam a rajzon is amit láthatsz, hogy az érintők helyett az a=1/2-ben csak bal és jobboldali érintők vannak (egy szögponttal van dolgunk, ahol a kél szélső derivált különböző de véges), ellenben mint olvashatod, a függvény azon a értékekre amelyekre (0,1) intervallumban vannak NEM KONVEX (Én is igazoltam, hogy kijön a konvexitás). Tehát az érintők alúl vannak és mégsem konvex? Tehát...???? Szerintem ezért nem helytálló ez a definició!
|
| Előzmény: [345] epsilon, 2008-03-05 10:23:25 |
|
|




 (0,1) a nyílt intervallumban van, akkor f nem deriválható x=a-ban, mert a két félérintő különböző szöget zár be: a balérintő meredeksége 2a+1, míg a jobbérintőé 2a-1. A balérintő mindig pozitív meredekségű és meredekebb, mint a jobbérintő. A függvény tehát nem lehet konvex.
(0,1) a nyílt intervallumban van, akkor f nem deriválható x=a-ban, mert a két félérintő különböző szöget zár be: a balérintő meredeksége 2a+1, míg a jobbérintőé 2a-1. A balérintő mindig pozitív meredekségű és meredekebb, mint a jobbérintő. A függvény tehát nem lehet konvex.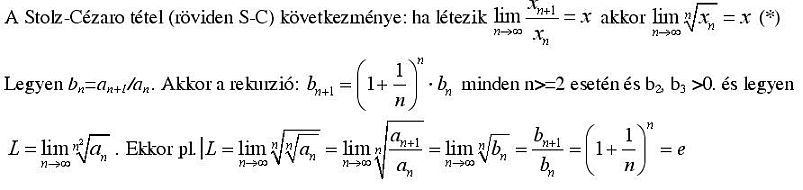
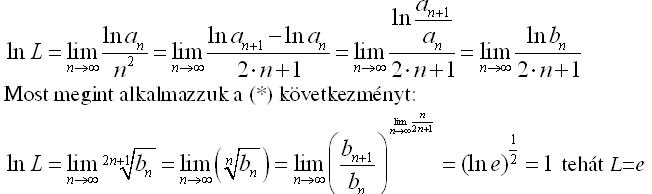
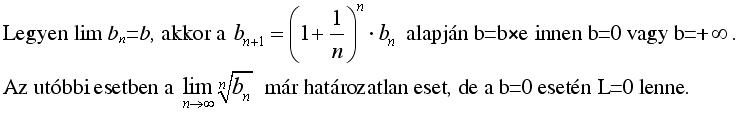



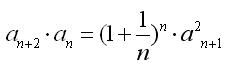
 >0-hoz létezik N, hogy
>0-hoz létezik N, hogy 
 is következhetne, nem?
is következhetne, nem?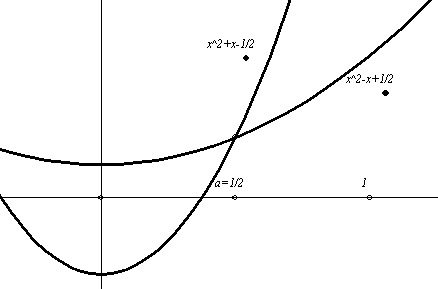


 R intervallumon értelmezett valós változójú függvény konvex, ha a függvénygörbe (bármely, az adott intervallumba eső ÿ(kiegészítés tőlem)) két pontját összekötő húr a függvénygörbe fölött halad ...
R intervallumon értelmezett valós változójú függvény konvex, ha a függvénygörbe (bármely, az adott intervallumba eső ÿ(kiegészítés tőlem)) két pontját összekötő húr a függvénygörbe fölött halad ...