|
| [1779] koma | 2012-10-29 20:33:02 |
 és azt leírnád esetleg,hogyan jött ki?
|
|
|
|
| [1782] koma | 2012-11-07 20:13:18 |
 Sziasztok!
Köszönöm szépen a válaszokat!(elnézést a kései üzenetért, de sajnos nagyon ritkán jutok internet kapcsolathoz)
Több fórumon azt olvastam, hogy a következő tanévtől állambácsi megszünteti a spec matekos tagozatokat(állítólag ez elhangzott a szegedi radnóti szülői értekezletén, más a fazekassal kapcsolatosan erősítette meg ezt a pletykát)
Ti tudtok erről valamit?
Nagyon félek tőle, hogy igaz a hír...
|
|
| [1783] sulc | 2012-11-07 21:03:08 |
 A hír téves. Ilyen tudtommal nem hangzott el a hétfői szülői értekezleteken. Szépen kérek mindenkit, hogy ne terjesszen ellenőrizetlen információkat! A következő tanévre is meg lesz hirdetve a 6 osztályos spec. mat. tagozatos osztály a szegedi Radnótiban. Schultz János, Radnóti Miklós Gimnázium, Szeged.
|
|
| [1784] HoA | 2012-11-08 17:46:06 |
 Vagyis - nem akarva csökkenteni egyikük matematikusi érdemeit sem - hasonlóan járt, mint Skljarszkij a Szovjetúnióban, mikor a háburú utáni évek kelet-európai hangulatában összekeverték a háború áldozatainak járó részvétet és tiszteletet a szakmai érdemekkel. Lásd Billiárdgolyók téma [63] .
|
| Előzmény: [1773] logarlécész, 2012-10-27 23:43:55 |
|
| [1785] Róbert Gida | 2012-11-11 17:55:57 |
 Én speciel már semmin nem csodálkoznék.
http://www.vg.hu/gazdasag/gazdasagpolitika/demjan-akar-assunk-godrot-hazaarulas-nem-lehivni-az-eu-penzeket-390676
"Demján meglátása szerint nem szabadna olyan tudósokat képezni, akik például a bogarak életét kutatják." Tippem szerint jövőre már nem indítanak biológia tagozatos osztályokat. Specmatosok is bármikor sorra kerülhetnek.
|
| Előzmény: [1783] sulc, 2012-11-07 21:03:08 |
|
| [1786] polarka | 2012-11-25 01:01:03 |
 Mely legkisebb n-re teljesül az egyenlőtlenség?
Több n-re behelyettesítve kaptam, hogy n>=8.
Viszont arra lennék kíváncsi, hogy próbálgatás nélkül hogyan lehetne a választ megkapni.
|
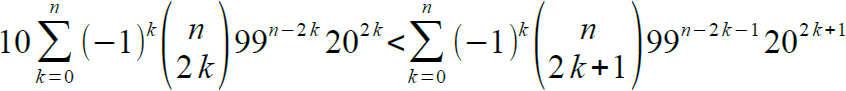 |
|
| [1787] Lóczi Lajos | 2012-11-25 12:51:31 |
 Nem mondtad meg, hogy n milyen számhalmaz eleme. Vegyük most természetes számnak az egyszerűség kedvéért.
Legyen például z a 99+20i komplex szám. Ekkor, valós és képzetes részeket használva, az egyenlőtlenség átírható a 10.re(zn)<im(zn) alakba. Polárkoordinátákkal folytatva, a
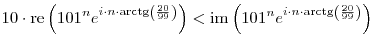
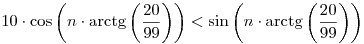
és
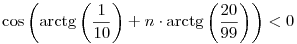
ekvivalens alakokat kapjuk. Mivel a koszinusz (n-ben) szigorúan monoton növő argumentuma n=0 esetén a (0, /2) intervallum eleme, a bal oldal akkor lesz először negatív, amikor az argumentum először belép a ( /2) intervallum eleme, a bal oldal akkor lesz először negatív, amikor az argumentum először belép a ( /2,3 /2,3 /2) intervallumba. Ez pedig n=8 esetén történik meg leghamarabb. /2) intervallumba. Ez pedig n=8 esetén történik meg leghamarabb.
|
| Előzmény: [1786] polarka, 2012-11-25 01:01:03 |
|
| [1788] Róbert Gida | 2012-11-25 12:57:23 |
 Egyrészt ordít róla a binomiális tétel, ki is lehet hozni egy explicit formulát mindkét oldalra. Komplex számokkal könnyebb az út, de ez valósban is megy. A Mathematica viszont egy érdekes alakot is ad a két oldal különbségére:
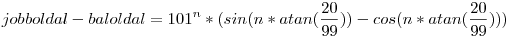
|
| Előzmény: [1786] polarka, 2012-11-25 01:01:03 |
|
|
| [1790] polarka | 2012-11-25 16:47:29 |
 Köszönöm a gyors választ!
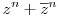 -t bontottam fel, hogy lássam mi is történik és ott próbáltam találgatni, hogy hogyan vonhatnám össze valamilyen (a+b)n alakban. Nem jutott eszembe az Re és Im szerinti felírás. -t bontottam fel, hogy lássam mi is történik és ott próbáltam találgatni, hogy hogyan vonhatnám össze valamilyen (a+b)n alakban. Nem jutott eszembe az Re és Im szerinti felírás.
Szerintem fölösleges a 3. egyenleted szerinti alakba való átalakítás. A második egyenletet folytatva:
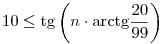
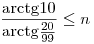
|
| Előzmény: [1787] Lóczi Lajos, 2012-11-25 12:51:31 |
|
| [1791] polarka | 2012-11-25 17:15:38 |
 Ezt hogyan csikartad ki a Mathematicából? Simplify vagy FullSimplify az alábbira nekem nem hozta ki:
Sum[(-1)^k Binomial[n, 2 k + 1] 99^(n - 2 k - 1) 20^(2 k + 1), k, 0, n] - 10*Sum[(-1)^k Binomial[n, 2 k] 99^(n - 2 k) 20^(2 k), k, 0, n]
|
| Előzmény: [1788] Róbert Gida, 2012-11-25 12:57:23 |
|
|
|
|
|
|
| [1797] Fálesz Mihály | 2012-11-26 06:52:29 |
 Nem olyan hosszú a bizonyítás.
(A Csebisev-polinomok helyett) azt a tn(x) polinomot érdemes vizsgálni, amire tn(2cos t)=2cos (nt) avagy  . Ez egy egész együtthatós polinom, a főegyütthatója 1, tehát a tn(x)=k alakú egyenletek (k egész) minden racionális gyöke egész. . Ez egy egész együtthatós polinom, a főegyütthatója 1, tehát a tn(x)=k alakú egyenletek (k egész) minden racionális gyöke egész.
Ebből azonnal következik, hogy ha x/ és cos x is racionális, akkor 2cos x értéke 0, és cos x is racionális, akkor 2cos x értéke 0,  1 vagy 1 vagy  2. 2.
A tangensre például a  azonossággal térhetünk át. azonossággal térhetünk át.
|
| Előzmény: [1796] Lóczi Lajos, 2012-11-26 00:11:36 |
|
|
|
|
|
|
|
|
|
| [1806] polarka | 2012-11-28 00:32:00 |
 Akkor a reláció iránya változna és n értékére maximumot kapnánk. Ami viszont az alap (fizikai) példát tekintve nem volna értelmes.
n jelöli azon ütközésszámot, amitől kezdve több ütközés nem lehetséges, értéke min 1.
Viszont belátom, hogy megéri az 1787. hozzászólásod 3. egyenlőtlensége szerinti cos-ra átalakítás.
|
| Előzmény: [1800] Lóczi Lajos, 2012-11-26 14:35:17 |
|
|
|
|
| [1810] polarka | 2012-11-28 10:28:25 |
 "Egy fal, két golyó. 1. golyó 1 egység tömeg a 2. golyó 100 egység. A fal van bal oldalt, tőle jobbra a könnyebb(kisebb) golyó, jobb oldalt a nagy, nehéz. A kis golyót 1 m/s sebességgel elindítjuk a nagy felé.
Elméleti feladat! Tökéletes rugalmas az ütközés! Nincs súrlódás! (gyakorlatban ilyen nincs) Kérdés, HÁNYSZOR ÜTKÖZIK A KIS GOLYÓ A NAGYNAK??"
|
| Előzmény: [1809] Lóczi Lajos, 2012-11-28 01:05:12 |
|
| [1811] Lapis Máté Sámuel | 2012-12-03 20:20:04 |
 Légyszíves segítsen valaki megoldani ezt a feladatot(megoldási menettel)!
2n+1 db egymást követő szám közül az első n+1 db szám négyzetének összege megyegyik a maradék számok négyzetének összegével. Melyek ezek a számok
|
|
| [1812] w | 2012-12-03 21:34:21 |
 Egy gyakran beváló jelölésmóddal "letaroljuk": Legyenek a számok a-n, a-(n-1), ..., a-1, a, a+1, ..., a+n. Felírva az egyenletet:
(a-n)2+(a-(n-1))2+...+a2=(a+1)2+(a+2)2+...+(a+n)2
(n+1)a2-2a(1+2+...+n)+(12+22+...n2)=na2+2a(1+2+...+n)+(12+22+...+n2)
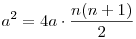
Ha a=0, ez azonosság. Ha a nem nulla, leosztunk vele:
a=2n(n+1).
Nem mondtad, hogy n tetszőleges-e vagy adott. Előbbi esetben csak a=0 felel meg, utóbbiban 2n(n+1) is. Ezek a gondolt számok.
|
| Előzmény: [1811] Lapis Máté Sámuel, 2012-12-03 20:20:04 |
|
|
| [1814] Hölder | 2012-12-06 00:56:23 |
 Van egy feladat,amivel nem boldogultam. Ha tudna valaki segíteni, az megköszönném. Igaz -e, hogy minden poliéder gráfjában van Hamilton-kör?
|
|
|
| [1816] Horváth Anett | 2013-01-16 18:30:21 |
 Sziasztok!
Van egy feladat amit nem tudok megoldani és ehhez szeretnék segítséget kérni: tangens 36 fok pontos értékének a kiszámítása, levezetése.
Előre is köszönöm a segítséget!
|
|
|
|
| [1819] Gizike | 2013-02-08 22:00:49 |
 Üdvözlet Mindenkinek!
Tudna valaki segíteni abban, hogy tudok "dobókocka" függvényt készíteni excelben? Nagyon várom a segítséget.
Szép napot!
|
|
| [1820] Lagrange | 2013-02-09 09:06:11 |
 Sziasztok! Valaki meg tudja mondani, hogy az SE(2) melyik Lie csoportot akarja jelenteni? SO(2), SU(2) meg SL(2)-ről hallottam, de ezt még nem sikerült kiderítenem.
|
|
| [1821] koma | 2013-02-09 10:28:06 |
 Sziasztok!
A napokban matekozgattam és felmerült egy kérdés bennem Ugyebár mindenki ismeri (a+b)2 kifejezést, amikor kifejtjük. Hogy fog ez kinézni pl 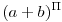 ? ?
Tehát irracionális kifejezést esetén mi történik? Egy lelkes amatőr vagyok, tehát ha buta kérdés, elnézést kérek...
|
|
| [1822] Maga Péter | 2013-02-09 10:52:24 |
 Nézd meg ezt! Az irányítástartó egybevágóságokról van szó, ami 2 dimenzióban az eltolások és forgatások összessége. A Lie-struktúrát, gondolom, úgy érdemes megadni, hogy az ember beágyazza GL(3)-ba zárt részcsoportként, és örökölteti a 3x3-as mátrixok sokaságstruktúráját.
|
| Előzmény: [1820] Lagrange, 2013-02-09 09:06:11 |
|
|
|
| [1825] Lapis Máté Sámuel | 2013-02-13 18:50:40 |
 Segítsen valaki megoldani ezt a feladatot a harmadfokú egyenlet megoldóképlete nélkül pls.
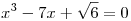
|
|
|
|





 1+1).(
1+1).(
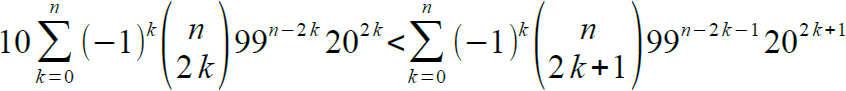

 /2) intervallum eleme, a bal oldal akkor lesz először negatív, amikor az argumentum először belép a (
/2) intervallum eleme, a bal oldal akkor lesz először negatív, amikor az argumentum először belép a (
 1 vagy
1 vagy 

