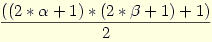| [352] epsilon | 2008-03-05 20:21:18 |
 OK cauchy, Én éppen félreértettelek, azt hittem, hogy amellett tartasz ki a 346-ban, hogy a feladatban OK az alulról húzott érintő (tehát alatta van), és konvex a (0,1)-en amit beláttunk, hogy nem igaz, holott figyelmetlenségem miatt elsiklottam afölött, hogy azt hangsúlyoztad ki, hogy az érintős definició sem mondott csődöt, szóval ennek örvendek, mert kezdett meginogni bennem, hogy amit sok éve tanítottak, most miért állna a fejére? De most már a szép esztétikus rajzod alapján is megnyugodtam ;-)
|
|
| [353] epsilon | 2008-03-06 06:43:23 |
 Helló Lajos! A megoldásodat még alaposan át kell sasoljam, mert addig értem, amíg a fogóba behelyezed, aztán látható, hogy az n a második hatványon kitevőt n×n-re lehet bontani, de azt nem értem, hogy a végén ahol megint n-edik gyök lenne, miért lett helyette éppen négyzetgyök? Hiszen eleinte olysami volt a bal oldalon pl. hogy (e-epsilon) az n-edik hatványon, de ha ebből n×n-edik gyököt vonok, hogyan lenne négyzetgyök??? A részleges határértékre térést értem, éppen ezen gondolkodtam el amikor megláttam, hogy Te is előbb csak n-edik gyököt vonsz, arra gondoltam, hogy még a hátramaradt n-edik gyökvonás ugyanazt jelenti, de mintha mégis másképpen kerülted ki. Üdv: epsilon
|
| Előzmény: [349] Lóczi Lajos, 2008-03-05 13:57:32 |
|
| [354] Lóczi Lajos | 2008-03-06 12:16:53 |
 Azért, mert e- kitevőjében lényegében az első k szám összege szerepel, ami nagyságrendileg k2/2, az alacsonyabb rendű tagok a limeszben eltűnnek. Ha ebből k2-edik gyököt vonsz, 1/2 marad. kitevőjében lényegében az első k szám összege szerepel, ami nagyságrendileg k2/2, az alacsonyabb rendű tagok a limeszben eltűnnek. Ha ebből k2-edik gyököt vonsz, 1/2 marad.
|
| Előzmény: [353] epsilon, 2008-03-06 06:43:23 |
|
| [355] epsilon | 2008-03-06 13:56:02 |
 Köszi Lajos! Így már semmi kétség nem fér hozzá! Üdv: epsilon
|
|
| [356] epsilon | 2008-03-07 13:26:44 |
 Helló! Újra jelentkezem, mert vagy elromlott a humorom, vagy mészlerakódásom van...vagy hibás a "helyes válasz"? Íme a feladatok:
|
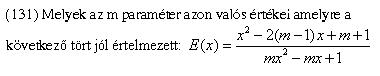 |
|
|
|
| [359] epsilon | 2008-03-07 13:29:17 |
 A hozzáfűznivalóim:
(131) Én arra gondoltam, hogy a nevezőnek ne legyenek valós gyökei, így a d<o ahonnan m a (0,4) intervallumhoz tartozik. A megadott helyes (?) válasz: más válasz (még választhatók voltak: R, 4, -1, (0,4).
(117) Sima számolásokkal kijött, hogy e=0, és ez (-1,1) között van. A megadott helyes (?) válsz: nem létezik semleges elem.
(277) Az x+y összeget S-el, az xy szorzatot P-vel jelöltem, és pl. ha az alsó 2 egyenletet megoldom, és a megoldás kell teljesítse az első egyenletet, akkor sem kapok intervallumot, és a helyes megoldás: [-3,-3]
Nektek mi a véleményetek? Előre is kösz, üdv: epsilon
|
|
| [360] epsilon | 2008-03-07 13:31:48 |
 Bocs a [-3,-3] elgépelés helyette [-3,-2]
|
|
|
| [362] epsilon | 2008-03-07 18:45:52 |
 Köszi cauchy! Hát igen, ez szép kis leégés, mert...rutinból csak x*e=x megoldása berögzült...:-( Szóval ez kilőve! Hátha a másik 2 nem éppen ilyen...
|
|
|
|
|
| [366] epsilon | 2008-03-08 09:25:34 |
 Helló cauchy! Nem kell általánosan minden x,y-ra szimmetrikus legyen, de speciálisan az e-re igen, mint írtad e*x=x*e és ez azt eredményezi, hogy e-x=x-e kellene legyen minden x-re a (-1,1) intervallumbóltehát, az alapötleted elegendő erre a speciális egyedi kommutativításra!
|
| Előzmény: [363] cauchy, 2008-03-07 18:48:00 |
|
| [367] epsilon | 2008-03-08 09:31:52 |
 (131)esetén nem kizárt, hogy [0,4) lenne a helyes megoldás, de csupán azon tűnődöm, hogy a "jól értelmezett" fogalomba belefér-e ez is, hogy a nevezőben levő másodfokú föggvény elsőfokúvá vagy álllandóvá fajuljon, de mivel erre nincs kikötés meglehet, hogy ez a megoldásod a jó. Számomra még az fura, hogy miért nem jön ki ez a 0 érték a tört létezési feltételből, hiszen akkor a létfeltétel d<0 helyett d<=0 és a nevezőnek ne legyen valós gyöke, nem de? Vagyis túl szinguárisan osont be ez a 0.
|
| Előzmény: [364] cauchy, 2008-03-07 19:07:15 |
|
| [368] epsilon | 2008-03-08 09:46:19 |
 (277)-nél, ha az általuk elfogadott -3 értéket behelyetesítem mindhárom egyenletbe, ez az ellentmondás jön ki: egyrészt xy=5 másrészt xy=-13/5. Amit Te mondasz, valóban az egyedüli, és jó is, mert ha az utolsó 2 egyenletet összeadtam (m+2)(x+y)=m+2 jön ki, és ha m+2 nem 0 akkor x+y=1 és a három egyenlet alapján egyrészt mxy=3 másrészt xy=2-m jön ki, marad m=-2 és erre az S=x+y=11 és P=xy=-17/2 és az ezzel felírt másodfokú egyenletnek van valós megoldása. Szerintem nagyon az a gyanúm, hogy ezúttal a könyvben tévedtek.
|
| Előzmény: [365] cauchy, 2008-03-07 22:15:03 |
|
| [369] Onkie | 2008-03-08 22:12:28 |
 Sziasztok!
Valaki el tudná küldeni e-mailben annak a tételnek a bizonyítását, hogy bármely tetszőleges négyszög oldalainak felezőpontjait összekötve paralelogrammát kapok? Az egész napomat a bizonyítással töltöttem, eredménytelenül... A segítséget előre is köszönöm! E-mail címem: xuli27@hotmail.com
U.i.: ha nem oldható meg az e-mailben való elküldés, e-mailben írd meg, hogy válaszoltál. Ez esetben is előre köszönöm a fáradozásokat!
|
|
| [370] Róbert Gida | 2008-03-08 22:27:36 |
 Halálismert példa. Legyen ABCD a négyszög. P az AB oldal felezőpontja, Q az BC oldalé, R a CD oldalé, S a DA oldalé. Ekkor a felezőpontok által meghatározott négyszög csúcsai sorrendben: PQRS. Az, hogy paralellogramma azzal ekvivalens, hogy a szemközti oldalai párhuzamosak, azaz PQ||RS és QR||SP kell. De PQ az ABC háromszög középvonala, így párhuzamos az alappal, ami az AC, továbbá RS a CDA háromszög középvonala, így párhuzamos az alappal, ami az AC. Ergó mindkettő párhuzmaos az AC-vel, így PQ és RS egymással is párhuzamosak. Hasonlóan QR és SP is párhuzamos. Ami kellett.
Standard megoldása egyébként vektorokkal van. Az is elemi.
|
| Előzmény: [369] Onkie, 2008-03-08 22:12:28 |
|
|
| [372] epsilon | 2008-03-09 19:24:31 |
 Talán a legrövidebb megoldás erre a feladatra az affixumokkal ( a csúcsokhoz rendelt komplex számokkal) van: Legyenek rendre a,b,c,d az ABCD négyszög csúcsainak affixumai, legyenek M,N,P,Q az AB, BC, CD, DA oldalak felezőpontok affixumai, ezért: m=1/2(a+b), n=1/2(b+c), p=1/2(c+d), q=1/2(d+a). Az MNPG paralelogramma <=> m+p=n+q ami azonnal adódik.
|
|
| [373] epsilon | 2008-03-17 14:28:05 |
 Helló! Ismét jelentkezem, egy jámbornak tűnő limesszel, hiába fejtettem ki a kombinációkat, egszerűsítés után sem találtam valami olyan alakra ami a megadot limeszértéket adja. (Ezt egyenlőre még nem mondanám meg, mert megint azt vadászom, vajon az eredmény jó-e?) Íme a limesz, és előre is kösz bármilyen jó tippet! Üdv: epsilon
|
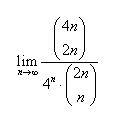 |
|
| [374] epsilon | 2008-03-17 14:41:38 |
 Közben még előkerültek a múlt héten függőben maradtak, íme még egy:245-ös. Tekintsük a lennebb látható egyenletet, minden n>=2 pozitív egészre. Melyek azok az n értékek, amelyekre az egyenletnek van legalább 1 pozitív egész megoldása? A válasz: 4s+3 ahol s nemnegatív egész, ellenben Én már n=3 esetén nem láttam az egész megoldást, hiszen ez a245=5×5×11 pozitív osztói közül való kell legyen. Nagyon gyanus ez az eredmény. Az lenne a kérdésem, hogy az n=4s+3 bár egy szükséges feltétel? Mert szerintem nem elégséges, vagy tévedek? Itt az egyenlet:
|
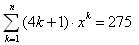 |
|
| [375] epsilon | 2008-03-17 14:45:58 |
 116-os: Minden n pozitív egész szám esetén jelölje Inv(n) azon (x,y) egész számpárok számát amelyek szimmetrizálhatók és amelyekre x×x+y×y=n×n. Mennyi a következő összeg értéke: Inv(1)+Inv(2)+Inv(3)+...+Inv(2005)
|
|
| [376] epsilon | 2008-03-17 14:59:13 |
 Helló cauchy! "(277) Nekem az jön ki, hogy m = -2." Ez hogyan jött ki, mert Nekem az m×m-2m+3=0 egyenlet jött ki, így nincs megoldás :-( valóban így lenne? "(131) Nem azért, mert [0, 4) a helyes?" Ez valóban teéjesen Ok, mert nem föltétlen muszáj, hogy a nevező 2-od fokú legyen, lehet "degenerált" is, és akkor nem szükséges a d<0 mert az már értelmetlen. Kösz az észrevételt! Üdv: epsilon
|
| Előzmény: [365] cauchy, 2008-03-07 22:15:03 |
|
|
|
|
| [380] epsilon | 2008-03-17 18:18:18 |
 Hát igen :-) kösz, "szász a lován ül és keresi" :-) szóval nem akartam belenyugodni, hogy nem talál az eredmény azzal amit a megoldásnál láttam, így másképpen próbálkozva, még az m=-2 is elveszett, de megtaláltam. Kösz!
|
| Előzmény: [379] cauchy, 2008-03-17 16:33:18 |
|
|
|
| [383] epsilon | 2008-03-18 06:41:43 |
 Ja: értem, mindjárt nem tudom a szorzótáblát sem :-( hiszen 245=5×5×11 helyesen 275=5×5×11, tehát sugalni akartam a 275 felbontását.
|
|
| [384] nadorp | 2008-03-18 09:52:09 |
 Valami nem stimmel. Nem írtad el a példát? Ui. a baloldal n>11 esetén minden pozitív egészre nagyobb 275-nél. Tehát n nem lehet 4s+3 végtelen sok s-re. Akkor lenne értelme, ha a baloldal mondjuk 275y lenne.
|
| Előzmény: [374] epsilon, 2008-03-17 14:41:38 |
|
| [385] epsilon | 2008-03-18 11:28:18 |
 Helló nadorp!Noha gyakran elpötyögök dolgokat :-( szerencsére, a lényeget nem írtam el, és fordításól van a feladat, átnéztem, és most is egyértelműen azt írja, hogy milyen n-re van pozutív egész gyöke, a válasz 4p+3, de ez szerintem nem jelenti azt, hogy MINDEN ILYEN n értékre, azért kérdeztem Tőúletek, hogy nem-e azt szeretnék tudni, hogy n milyen alakú kell legyen (szükséges feltétel) mert esetleg nem mondhatnak többet??? (pl. oszthatósági szempontból) az n-ről. Szóval valahogy meg szeretném tudni, hogy egyáltalán van-e ilyen n, ha van hány, azok meg valóan szükségszerűen 4p+3 alakúak kell legyenek? Talán így megmenthető a feladat, mert másképpen ....nem látom mit is lehetne izonyítani? Üdv: epsilon
|
| Előzmény: [383] epsilon, 2008-03-18 06:41:43 |
|
| [386] epsilon | 2008-03-24 09:56:10 |
 Helló! Megint van egy feladatom, valakinek van-e valami jó ötlete? Kösz, üdv: epsilon
|
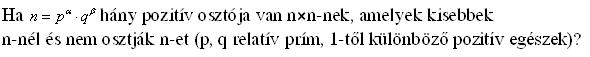 |
|
|
|
|
|
| [391] epsilon | 2008-03-24 11:42:42 |
 Köszi Róbert Gida! Profi munka, és mégis elemi. A társosztóról röviden a lényeget hol olvashatom el pl. a neten, vagy elmondod-e egy pár szóban, mert a következő képlet nem jön be :-( Üdv: epsilon
|
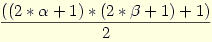 |
| Előzmény: [390] Róbert Gida, 2008-03-24 11:30:35 |
|
| [392] Róbert Gida | 2008-03-24 11:55:23 |
 [Számlálóban a legkülső zárójel persze felesleges]
n egész, d osztója, akkor d társosztója n/d, azaz d és e osztó-társosztó, ha d*e=n teljesül, ekkor persze e társosztója d, így az osztók párokba rendezhetőek (előfordulhat, hogy önmaga lesz a társosztó, ha n négyzetszám. Például n=36 osztó-társosztó listája:
(1,36),(2,18),(3,12),(4,9),(6,6)
Ha ezt egy négyzetszámra végzed el: k2=d*e, akkor minden párban pontosan az egyik lesz legfeljebb k, kivéve, ha k=d=e, ez triviális, így a k-nál nem nagyobb osztók száma=k2 osztópárjainak a száma= , ha , ha 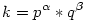 , akkor ebben az esetben ez , akkor ebben az esetben ez 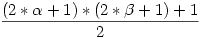
|
| Előzmény: [391] epsilon, 2008-03-24 11:42:42 |
|
|
| [394] Korrob | 2008-03-25 17:26:39 |
 Szervusztok! Nem vagyok valami jó matekból Elsőfokú diofantoszi egyenletekre kéne általános megoldás. ilyenekre pl.: xy=x+y 3x+7y=19 102x+45y=53 stb.
Előre is köszi.
|
|
| [395] Sirpi | 2008-03-25 17:46:59 |
 A 2. és a harmadik ugyanolyan típusú, a 2-esen mutatom meg, hogy megy a dolog. Kell találnod egy megoldást, ilyen pl. az x=4, y=1. Ezt pl. meg lehet úgy tenni, hogy a 19-ből 7-esével lépkedsz lefelé (felfelé), és figyeled, mikor jutsz 3-mal osztható számhoz.
Ha megvan egy megoldás, fel kell használni, hogy ha x és y megoldás, akkor x+7 és y-3 is az, vagyis a megoldások: 4+7k, 1-3k. Behelyettesítve: 3(4+7k)+7(1-3k)=12+21k+7-21k=19, tehát tényleg megoldások.
Az első pedig elég közismert:
xy=x+y
xy-x-y+1=1
(x-1)(y-1)=1
Innen rögtön kijön, hogy tetszőleges x esetén 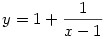 , valósokra ezzel meg is oldottuk a feladatot. Ha azt is feltesszük, hogy mindkettő egész, akkor is könnyű dolgunk van, ugyanis az 1 csak 1.1 és (-1).(-1) alakban bomlik két egész szám szorzatára, innen a megoldások: x=y=0 és x=y=2. , valósokra ezzel meg is oldottuk a feladatot. Ha azt is feltesszük, hogy mindkettő egész, akkor is könnyű dolgunk van, ugyanis az 1 csak 1.1 és (-1).(-1) alakban bomlik két egész szám szorzatára, innen a megoldások: x=y=0 és x=y=2.
|
| Előzmény: [394] Korrob, 2008-03-25 17:26:39 |
|
|
|
| [398] Sirpi | 2008-03-26 16:31:32 |
 A 3.-at annyival egészíteném én ki, hogy mivel a 45 és a 102 lnko-ja 3, ezért azzal rögtön le lehet osztani:
34x+15y=53/3
Vagyis nincs egész megoldás, mert a bal oldal biztos egész, a jobb meg nem.
|
| Előzmény: [396] BohnerGéza, 2008-03-26 10:32:40 |
|
|
| [400] csewe | 2008-04-02 17:02:09 |
 sziasztok
meg kellene oldanom ezt az egyenletet
n = x*(x + 1)
n pozitív egész pl:30 , 42 , 50 stb
szeretném megkapni x - et
persze nem ezeknél a kis számoknál okoz gondot a dolog
ha valaki tudja legyenszives vezesse le nekem a megoldást
köszi
|
|
|




 kitevőjében lényegében az első k szám összege szerepel, ami nagyságrendileg k2/2, az alacsonyabb rendű tagok a limeszben eltűnnek. Ha ebből k2-edik gyököt vonsz, 1/2 marad.
kitevőjében lényegében az első k szám összege szerepel, ami nagyságrendileg k2/2, az alacsonyabb rendű tagok a limeszben eltűnnek. Ha ebből k2-edik gyököt vonsz, 1/2 marad.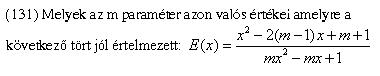
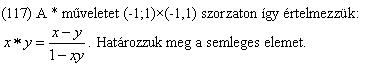
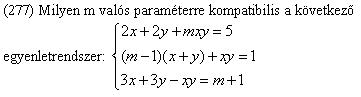

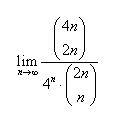
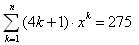
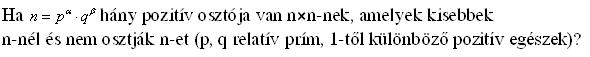

 +1)*(2*
+1)*(2* +1) pozitiv osztója van. Osztó társosztó fogalmát használva ezek közül
+1) pozitiv osztója van. Osztó társosztó fogalmát használva ezek közül