Szerk
A KöMaL egy példányának ára 2025. szeptembertől 1600 Ft, előfizetése 1 évre 12500 Ft – BJMT tagoknak 12000 Ft.
Megrendelem
A Középiskolai Matematikai és Fizikai Lapok évről évre bővülő számú évfolyama – jelenleg 1893–1901-ig és 1965 és 2019 között – többféle szempont szerint kereshető, és a kiválogatott feladatok, cikkek kinyomtathatóak. Az összetett kereséssel igazi kincsestárban kutathatnak ingyenesen az olvasók: lehet keresni cikkekben és feladatokban többek között cím, szöveg, kategória (pl. versenyek), témakör és név alapján.
Jelen kötetünk 24 olyan feladatsorból áll, amelyek 2007 és 2017 között jelentek meg a KöMaL-ban. A feladatsorok összeállítói gyakorló tanárok, szakértők, vezető tanárok, tankönyvszerzők:
A KöMaL-t Arany Dániel alapította 1893-ban, hogy tartalomban gazdag példatárat adjon tanárok és tanulók kezébe. Azóta matematikusok és tudósok több generációja csiszolta problémamegoldó képességét a KöMaL révén.
Azok is figyelmesen olvassák el a Versenykiírást, akik tavaly már részt vettek versenyünkben.
Idén is matematikából, fizikából és informatikából indítunk versenyeket. Egyénileg, illetve csapatban is lehet versenyezni, a versenyek 9 hónapon keresztül, 2025. szeptemberétől 2026. június elejéig tartanak. Minden hónapban új feladatokat tűzünk ki, és a megoldásokat a következő hónap elejéig küldheted be. A verseny végeredményét a 2026. szeptemberi számunkban hirdetjük ki. A díjakat jövő ősszel, a KöMaL Ifjúsági Ankéton adjuk át.
Feldolgozottság: 65.0% (234 feladatból 152)
Az Európai Unió Általános Adatvédelmi Rendelete értelmében 16 évesnél versenyzőink adatait csak a szülő vagy törvényes képviselő hozzájárulásával kezelhetjük. Ezért fiatal versenyőinktől egy szülői hozzájárulást kérünk az adatkezeléshez; amíg nem érkezik meg a szülői nyilatkozat, addig a regisztrációjuk nem érvényes.
A 16 évesnél fiatalabbak regisztrációjakor lehetőséget adunk az egyik szülő nevének és e-mail címének megadására. A szülőnek e-mailt küldünk, és biztosítjuk, hogy a szükséges nyilatkozatot néhány perc alatt megtehesse.
A KöMaL kiadásának, a versenyek teljes lebonyolításának, díjazásának és a díjkiosztóval egybekötött Ifjúsági Ankétok szervezésének költségeit 2007 óta a MATFUND Középiskolai Matematikai és Fizikai Alapítvány fizeti.
Kérjük, személyi jövedelemadója 1%-ának felajánlásával álljon a több, mint 125 éve alapított Középiskolai Matematikai és Fizikai Lapok mellé!
Matfund
A MATFUND Alapítvány pénzügyi feladata és célja, hogy hosszú távon megoldja a Középiskolai Matematikai és Fizikai Lapok Informatika rovattal című folyóirat stabil finanszírozását. Az elmúlt 25 évben évről évre folyamatosan változó feltételű pályázatokból és támogatásokból tudtuk fenntartani a lapot, bizonytalan anyagi körülmények között.
Szilassi Lajos
Nem kell túl sokáig keresgélnünk az interneten a fejtörő feladatok között ahhoz, hogy sík vagy tér kitöltésére vonatkozó feladványra bukkanjunk. Ezek egyik fajtája az, amikor néhány síkidom vagy test valamilyen keretben van elhelyezve úgy, hogy látszólag teljesen kitöltik azt, de van még külön egy további eleme a játéknak.
Hujter Bálint
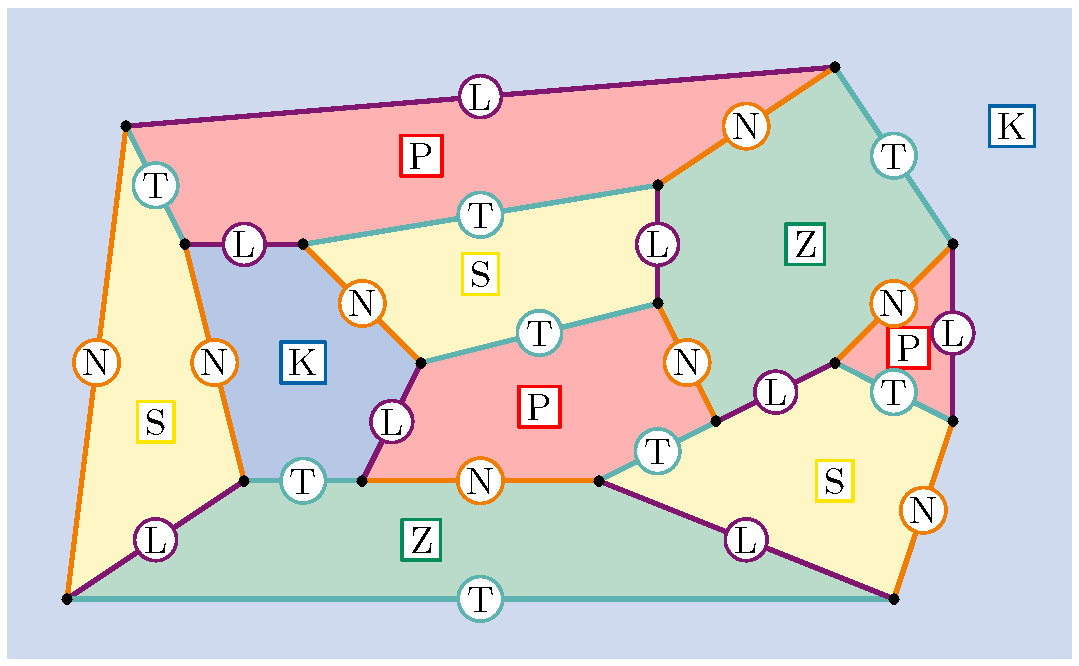
A KöMaL 2025 szeptemberi számában (Tait tétele és a 3-reguláris gráfok – a B. 5403. feladat háttere) kimondtuk Tait alábbi tételét.
Tétel (Tait tétele). Legyen \(\displaystyle G\) egy 3-reguláris, hídélmentes, síkbarajzolt gráf. Ekkor \(\displaystyle G\) tartományai \(\displaystyle 4\)-színezhetők akkor és csak akkor, ha élei \(\displaystyle 3\)-színezhetők.
A tételben \(\displaystyle k\)-színezésen olyan színezést értünk, amely \(\displaystyle k\)-féle színt használ, és az egymással szomszédos tartományok (illetve élszínezés esetén az egy csúcsban találkozó élek) mindig különböző színűek.
A szeptemberi számba nem került be a tétel bizonyítása (azzal a céllal, hogy akinek van kedve, gondolkodhasson rajta), ezt most pótoljuk.
Vígh Viktor
Legutóbb szeptemberi számunkban foglalkoztunk bújócska típusú ördöglakatokkal. Elkészítésre ajánlottunk olvasóinknak egy pálcás változatot, ahol a ,,szokásos'' trükk nem működik, mivel az átbújtatás után (lásd ábra) a pálca nem fér át a hurkon a zsinór rövidsége miatt. Azonban vegyük észre, hogy ebben az átbújtatott állapotban valójában annyi a célunk, hogy a hurok a dupla zsinór másik oldalára kerüljön. Ezt úgy is elérhetjük, ha a téglatest formájú ,,alapot'' bújtatjuk át a hurkon.
Tatár Zsuzsanna Mária (Esztergom)
1. Határozza meg a természetes számok halmazának azt a legbővebb részhalmazát, amely értelmezési tartománya lehet az alábbi kifejezéseknek.
a) \(\displaystyle \log_x(-2x^2-7x+15)\) (6 pont)
b) \(\displaystyle \sqrt{\dfrac{x^2-2x}{-2x^2- 7x+15}}\) (6 pont)
Jócsik Csilla (Győr)
1. a) Oldja meg a következő egyenletet az egész számok halmazán:
\(\displaystyle (x^2-9)\left(\dfrac{1}{x-3}-\dfrac{1}{x+3}-1\right)=9+x \)
b) Egy négyszög \(\displaystyle \alpha\) szögére teljesül, hogy \(\displaystyle 4\sin^2\alpha-3=0\). Mekkora lehet az \(\displaystyle \alpha\) szög nagysága?
Fonyó Lajos, Fonyóné Németh Ildikó
A Rátz László vándorgyűlésen rendezett verseny feladatai
1. Az Azariah koncertre jegyet vásárlók sorában Dávid elölről a 2024., hátulról a 2025. várakozó. Hány ember áll a sorban?
(A) 4047; (B) 4048; (C) 4049; (D) 4050; (E) 4051
2. Dia és Viki egy táblán meglát néhány számot. Dia minden számhoz hozzáad 3-at, majd megállapítja, hogy a kapott számok összege 45. Viki az eredetileg a táblán szereplő számokat megszorozza 3-mal, és meglepődve állapítja meg, hogy az általa kapott számok összege is 45. Hány szám volt felírva a táblára a lányok érkezésekor?
(A) 10; (B) 9; (C) 8; (D) 6; (E) 5
Pálfy Péter Pál
A magyar matematika egyik fellegvára – az egyetemek mellett – a Rényi Alfréd Matematikai Kutatóintézet. Az intézetet 1950-ben alapították a Magyar Tudományos Akadémia Alkalmazott Matematikai Intézete néven. A kommunista ideológia szerint ,,a tudomány közvetlen termelőerővé válik'', ennek megfelelően az intézet feladata a népgazdaság fejlődésének segítése volt a tudomány eszközeivel. Az intézet vezetésével az akkor mindössze 29 éves sztármatematikust, Rényi Alfrédot bízták meg. Rényi bölcsen hagyta, hogy a kötelező feladatok elvégzése mellett az intézetbe toborzott kiváló matematikusok elméleti kérdésekkel is foglalkozzanak, hiszen az alkalmazott és az elméleti matematika összetartozik, együtt művelve a két irányt sokkal eredményesebb lesz a munka. Ezt az Akadémia vezetésével is sikerült elfogadtatnia, ennek megfelelően már 1955-ben a Matematikai Kutató Intézet elnevezés került a cégtáblára. Rényi Alfréd sajnos korán, 49 évesen elhunyt. Az intézet 1999 óta viseli alapító igazgatójának a nevét.
C. 1844 Ági pirossal, Laci kékkel színezgeti egy \(\displaystyle n \times n\)-es (\(\displaystyle n>1\)) fehér táblázat mezőit, amely \(\displaystyle i\)-edik sorának \(\displaystyle j\)-edik mezőjét \(\displaystyle (i;j)\)-vel jelöljük. Első lépésben Ági pirosra festi a főátló (bal felsőtől a jobb alsóig) mezőit. Ezután felváltva jönnek: ha Laci \(\displaystyle (i;j)\)-t színezi, akkor Ági \(\displaystyle (j;i)\)-t. Minden mezőt pontosan egyszer színeznek be. A \(\displaystyle k\)-adik sort különlegesnek hívjuk, ha bármely kék \(\displaystyle (k;j)\) esetén létezik \(\displaystyle l\), hogy \(\displaystyle (k;l)\) és \(\displaystyle (l;j)\) is piros. Bizonyítsuk be, hogy a színezgetés végeztével Ági talál különleges sort.
Javasolta: Paulovics Zoltán (Budapest)
C. 1865. Az iskolai szkanderbajnokságon \(\displaystyle 17\) fő indult el. Mindenki pontosan egyszer mérkőzött meg mindenkivel, döntetlen nem született. A versenyzők egy csoportját erősnek hívjuk, ha teljesül rájuk, hogy bármely rajtuk kívüli versenyzőt legyőzött közülük valaki. Bizonyítsuk be, hogy kiválasztható legfeljebb \(\displaystyle 9\) fős erős csoport.
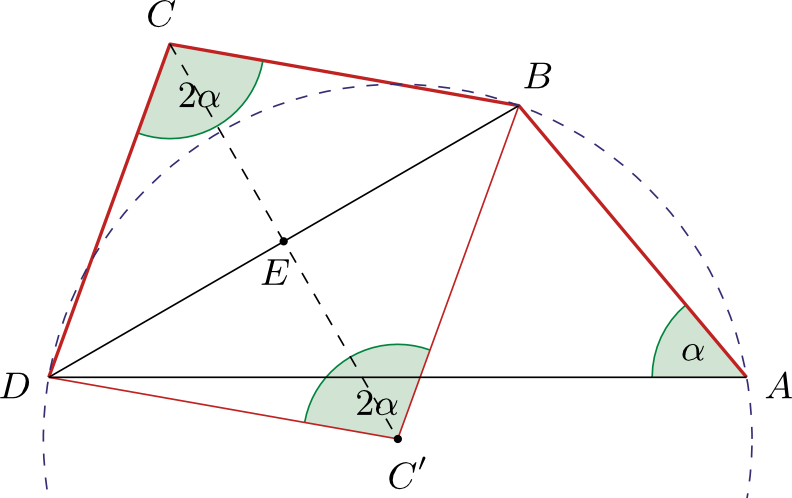
B. 5472. Az \(\displaystyle ABCD\) konvex négyszögben \(\displaystyle AB=BC=CD\). Igazoljuk, hogy ha \(\displaystyle BCD\sphericalangle=2DAB\sphericalangle\), akkor \(\displaystyle ABC\sphericalangle=2CDA\sphericalangle\).
Javasolta: Kós Géza (Budapest) és Vígh Viktor (Sándorfalva)
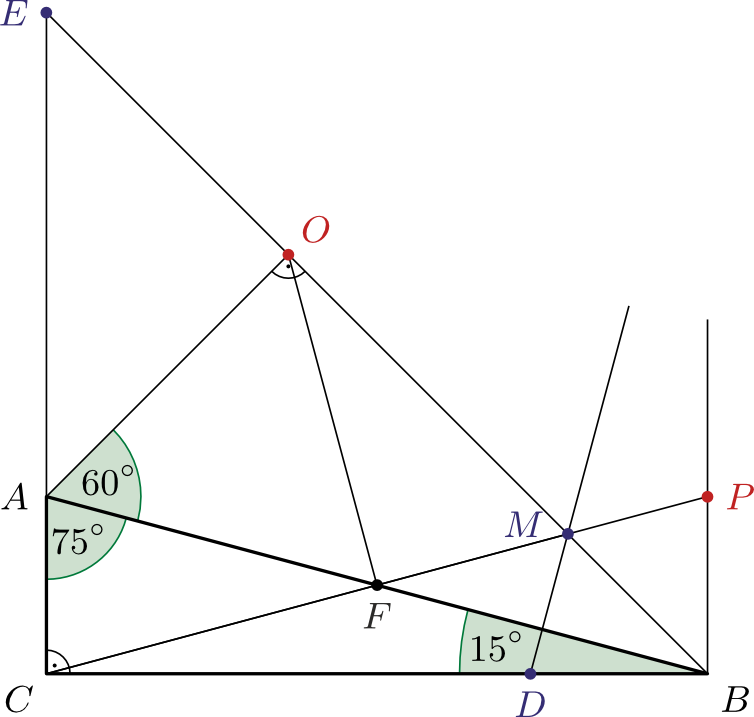
B. 5489. Az \(\displaystyle ABC\) derékszögű háromszögben \(\displaystyle ABC\sphericalangle=15^\circ\) és \(\displaystyle CAB\sphericalangle=75^\circ\), továbbá az \(\displaystyle AB\) átfogó felezőpontja \(\displaystyle F\). A \(\displaystyle BC\) befogón vegyük fel a \(\displaystyle D\) pontot úgy, hogy \(\displaystyle BD=CA\), a \(\displaystyle CA\) félegyenesen az \(\displaystyle A\) ponton túl az \(\displaystyle E\) pontot úgy, hogy \(\displaystyle CE=BC\) teljesüljön. A \(\displaystyle BE\) és \(\displaystyle CF\) egyenesek metszéspontja legyen \(\displaystyle M\). Bizonyítsuk be, hogy a \(\displaystyle DM\) és \(\displaystyle CM\) egyenesek érintik az \(\displaystyle AEF\) háromszög köré írt kört.
Javasolta: Bíró Bálint (Eger)
C. 1842. Oldjuk meg a valós számok halmazán a \(\displaystyle 9^x+(6x-23)\cdot 3^x+5x^2-39x+76=0\) egyenletet.
Javasolta: Bencze Mihály (Brassó
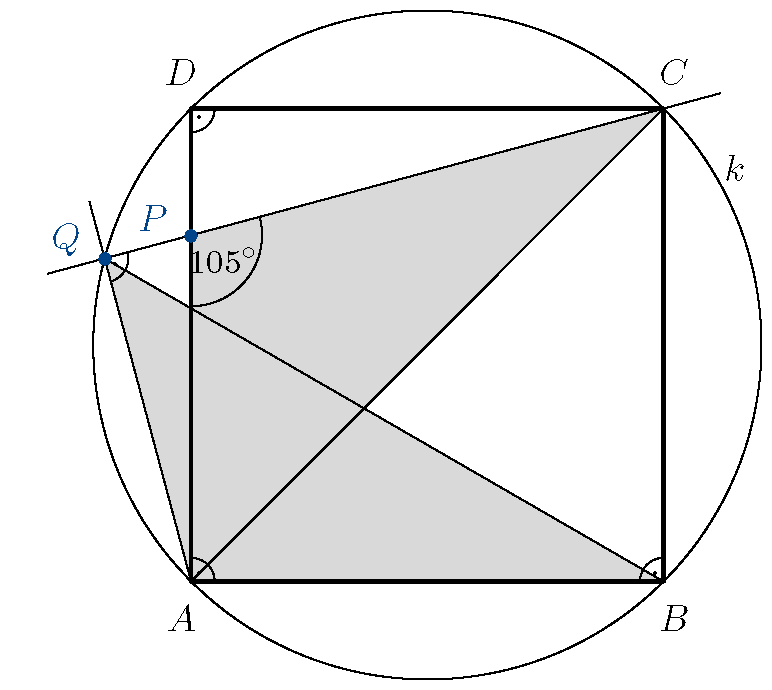
C. 1847. Az \(\displaystyle ABCD\) négyzet \(\displaystyle AD\) oldalán válasszuk ki úgy a \(\displaystyle P\) pontot, hogy \(\displaystyle CPA\sphericalangle=105^{\circ}\) legyen. A \(\displaystyle CP\) egyenesre az \(\displaystyle A\) pontból bocsássunk merőlegest, amelynek talppontját jelölje \(\displaystyle Q\). Határozzuk meg az \(\displaystyle ABQ\) és az \(\displaystyle ACP\) háromszögek területe arányának pontos értékét.
Javasolta:Bíró BálintEger
C. 1853. Néhány kutató egy virágos homokgyepen zümmögő poszméhek ötvenfős csapatát figyeli. Izgatottan állapítják meg, hogy a poszméhek mindegyike pontosan négyféle virágról gyűjtött virágport, mielőtt továbbrepült volna. Sőt, még azt is feljegyezték, hogy mindegyik poszméh különböző négyest választott, de mind az \(\displaystyle 50\) poszméh meglátogatott egy buglyos fátyolvirágot. Bizonyítsuk be, hogy összesen legalább 9-féle virágról gyűjtöttek a poszméhek.
Javasolta:Paulovics ZoltánBudapest
C. 1855. Egy \(\displaystyle 19\) drónból álló csapat repül egy gyakorlótér felett, a biztonsági előírásoknak megfelelően olyan rögzített alakzatban, ahol bármely két gépnek különböző a távolsága. Egy hackertámadás következtében a drónok egymásra nyitnak tüzet: mindegyik drón lő egyet a hozzá legközelebbi drónra, és ezzel megsemmisíti azt. (Feltételezzük, hogy minden drón tudott lőni, a drónok pontszerűnek tekinthetők, továbbá hogy a drónok csak azután semmisülnek meg, miután minden golyó becsapódott.)
Van-e köztük túlélő drón?
Egy drónt legfeljebb hány azonos (őt is tartalmazó) síkból származó lövedék találhatott el?
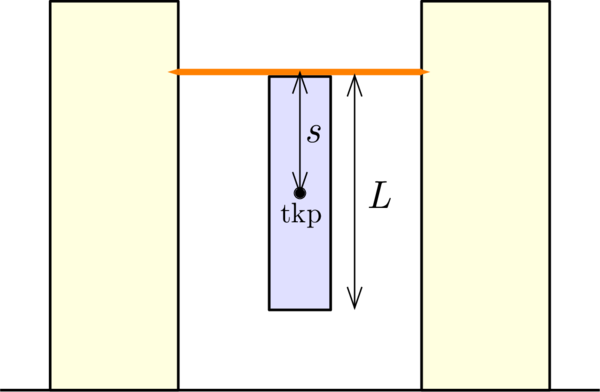
M. 444. Határozzuk meg egy AA-s ceruzaelem szimmetriatengelyére és egy arra merőleges, a tömegközépponton áthaladó tengelyre vett tehetetlenségi nyomatékait!
Közli: Széchenyi Gábor, Budapest
Megoldás. Az elem tömege (konyhai mérleggel mérve): \(\displaystyle m=24~\mathrm{g}\), hossza \(\displaystyle L=48~\mathrm{mm}\), átmérője (digitális tolómérővel mérve): \(\displaystyle d=14{,}2~\mathrm{mm}\), amiből a sugara: \(\displaystyle {r=d/2=7{,}1~\mathrm{mm}}\). A mérés során a szimmetriatengelyre vonatkozó \(\displaystyle \Theta_\parallel\), illetve az arra merőleges tengelyre vonatkozó \(\displaystyle \Theta_\perp\) tehetetlenségi nyomatékot egy-egy egymástól eltérő módszerrel mérjük meg.
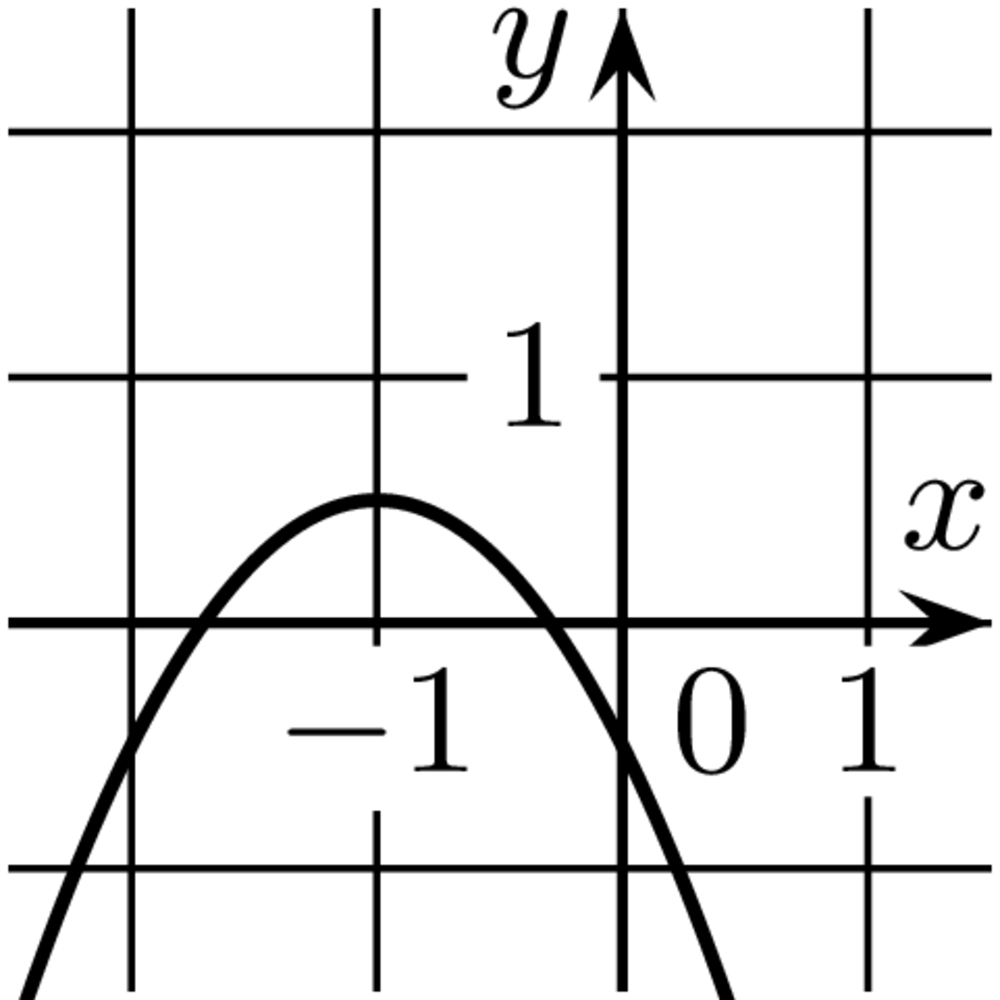
P. 5634. Egy rajztábla és egy rajta nyugvó könyv között a súrlódási együttható \(\displaystyle \mu\). A rajztábla egyik szélét lassan emeljük.
a) Mekkora \(\displaystyle \alpha\) hajlásszög esetén csúszik meg a könyv?
b) Mekkora a tábla \(\displaystyle 2\alpha\) hajlásszögű helyzetében a lecsúszó könyv gyorsulása?
c) Mekkora az a legkisebb vízszintes gyorsulás, amivel a \(\displaystyle 2\alpha\) hajlásszögű táblát előre kellene tolni ahhoz, hogy a könyv ne csússzon meg?
A csúszási és a tapadási súrlódási együtthatót tekintsük egyenlőnek. Az eredményeket \(\displaystyle \mu\) és \(\displaystyle g\) segítségével adjuk meg.
(5 pont)
Közli: Honyek Gyula, Veresegyház
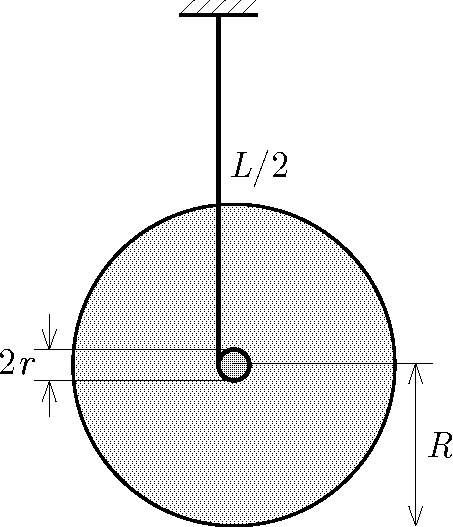
P. 5669. Egy \(\displaystyle R=5~\mathrm{cm}\) sugarú, \(\displaystyle m=0{,}5~\mathrm{kg}\) tömegű, homogén anyageloszlású tárcsa \(\displaystyle r=0{,}5~\mathrm{cm}\) sugarú tengelyéhez egy \(\displaystyle L=20~\mathrm{cm}\) hosszúságú, vékony fonál egyik végét rögzítjük, és a fonál \(\displaystyle L/2\) hosszúságú részét a tengelyre feltekerjük. A függőleges fonál másik végét rögzített helyzetben tartva a tárcsát elengedjük.
a) Mekkora erő feszíti a fonalat az egyenletesen gyorsuló tárcsa (,,jojó'') mozgása közben?
b) Mekkora a tárcsa tengelyének sebessége a fonál kitekeredésének pillanatában?
c) A tárcsa függőleges mozgásának megfordulásakor a fonalat feszítő erő egy rövid időre megnő (a tárcsa ,,ránt egyet'' a fonálon). Becsüljük meg a fonálerő átlagos értékét a rántás alatt!
P. 5667. Az ábrán egy izzólámpa látható két homorú tükör között. A jobb oldali tükör párhuzamos fénynyalábot állít elő, míg a bal oldali, kis méretű tükör megakadályozza, hogy az izzólámpa fényének jelentős része kiszökjön ebből az összeállításból, ami egy gépkocsi reflektorának felel meg.
P. 5664. Sokszor halljuk, hogy a sarkokon olvadó jég lassítja a Föld tengely körüli forgását. Becsüljük meg a jelenség nagyságát! Az Antarktisz területe \(\displaystyle 14~\textrm{millió~km}^2\), az Arktisz jégtakaróját is tekintsük ugyanekkorának. Vizsgáljuk azt, ha a Déli, illetve az Északi sarkon 1 m vastagságban elolvad a jég.
a) Mennyivel változik a tengerszint az egyik és a másik esetben? b) Mennyivel változik egy földi nap hossza?
P. 5651. Egy szigetelt, egyenletesen \(\displaystyle \sigma\) felületi töltéssűrűséggel rendelkező szabályos háromszög alakú lap minden oldala \(\displaystyle \sqrt{2}a\) hosszúságú. Mekkora az elektromos térerősség értéke abban a pontban, amely minden csúcsponttól \(\displaystyle a\) távolságra helyezkedik el?
P. 5646. Űrutazást terveznek a Marsra. Az űrhajó a Földet elhagyva olyan ellipszis pályára áll, amely érinti a két bolygópályát, perihéliumába esik a felszállás, aphéliumába pedig a megérkezés. A visszaút hasonló ellipszispályán történik. Az induláshoz mindkét esetben ki kell várni, amíg a két bolygó megfelelő helyzetbe kerül. Mennyi ideig tart az oda-, illetve visszaút, és legalább mennyi időt fognak a Marson tölteni? A bolygópályákat tekintsük azonos síkban fekvő köröknek, a Mars keringési ideje \(\displaystyle 687{,}0\) földi nap.
Közli: Vladár Károly, Kiskunhalas
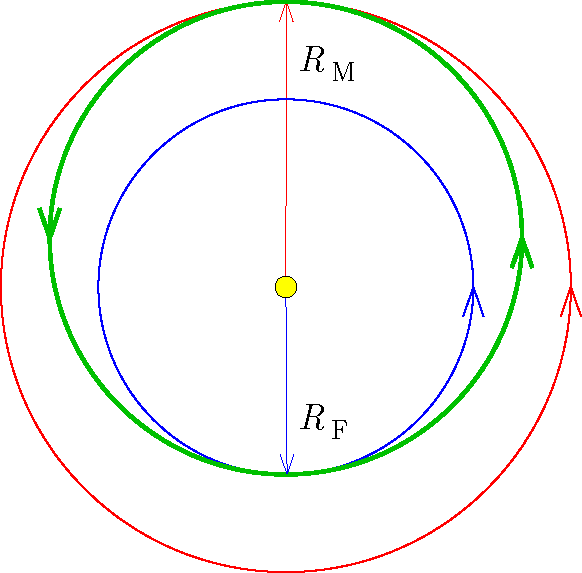
Megoldás. A Mars keringési ideje \(\displaystyle T_{\mathrm{M}}=687{,}0~\textrm{nap}=1{,}881~\textrm{év}\). Kepler III. törvénye alapján a Mars-pálya sugara:
\(\displaystyle \frac{R_{\mathrm{M}}^3}{T_{\mathrm{M}}^2}=\frac{R_{\mathrm{F}}^3}{T_{\mathrm{F}}^2},\quad\Rightarrow\quad R_{\mathrm{M}}=\sqrt[3]{\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{F}}}\right)^2}R_{\mathrm{F}}=1{,}524~\mathrm{CsE}, \)
ahol \(\displaystyle R_\mathrm{F}=1\,\mathrm{CsE}\) a Föld-pálya sugara és \(\displaystyle T_\mathrm{F}=1\,\textrm{év}\) a Föld keringési ideje.
1. ábra
Az oda- és visszaút ellipszispályájának félnagytengelye:
\(\displaystyle a=\frac{R_{\mathrm{M}}+R_{\mathrm{F}}}{2}=1{,}262~\mathrm{CsE},\)
amelyen a keringési idő (ismét Kepler III. törvénye alapján):
\(\displaystyle \frac{a^3}{T^2}=\frac{R_{\mathrm{F}}^3}{T_{\mathrm{F}}^2},\quad\Rightarrow\quad T=\sqrt{\left(\frac{a}{R_{\mathrm{F}}}\right)^3}T_{\mathrm{F}}=1{,}418~\textrm{év}. \)
Az oda- és visszaút időtartama egyaránt ennek az időnek a fele:
\(\displaystyle t=\frac{T}{2}=0{,}709~\textrm{év}\approx 259~\mathrm{nap}. \)
Az űrhajót akkor lehet visszaindítani, ha a \(\displaystyle t\) ideig tartó visszaút után éppen a Földdel egyszerre ér az ellipszis napközeli pontjába. A 2. ábrán az odaút indulásának és megérkezésének, valamint a visszaút indulásának pillanata látható.
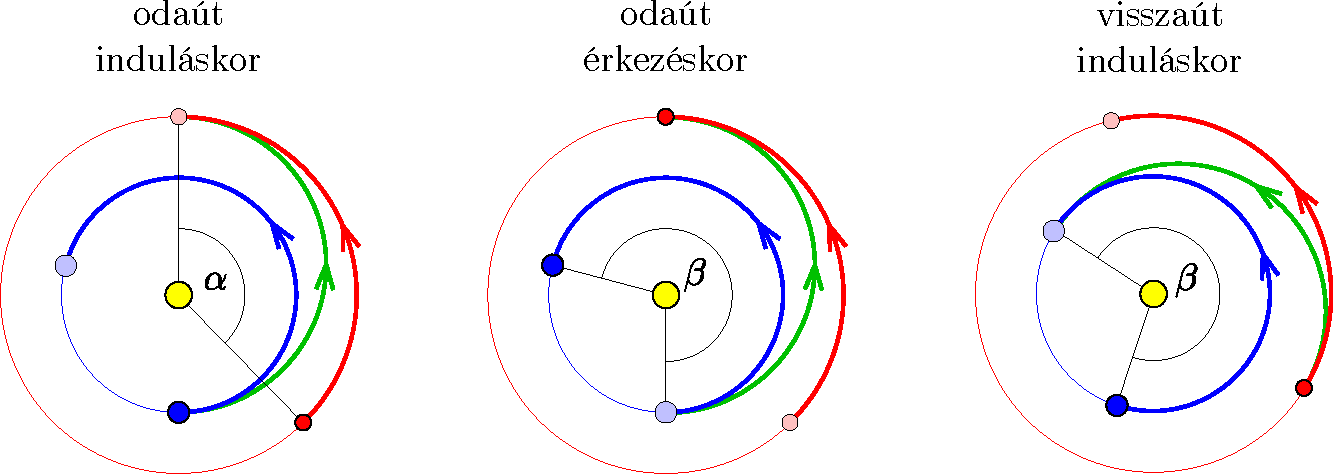
2. ábra
Az odautazás indulásakor a Mars még \(\displaystyle \alpha=\tfrac{360^\circ}{T_{\mathrm{M}}}\,t=135{,}7^\circ\)-kal a találkozási pont előtt jár. Mire az űrhajó pontosan fél fordulat után eléri a Marsot, a Föld \(\displaystyle \beta=\tfrac{360^\circ}{T_{\mathrm{F}}}\,t=255{,}2^\circ\)-ot tesz meg a pályáján, így a Föld ekkor \(\displaystyle \beta-180^\circ=75{,}2^\circ\)-kal jár a Mars előtt. Emiatt a visszainduláskor a Marsnak kell ugyanekkora szöggel a Föld előtt járnia. Tehát a Földnek az űrhajó megérkezése és visszaindulása között a Marshoz viszonyítva
\(\displaystyle \gamma=360^\circ-2(\beta-180^\circ)=209{,}6^\circ \)
szöget kell elfordulnia a Nap körül. A két bolygó relatív szögsebessége
\(\displaystyle \omega_{\mathrm{rel}}=\frac{360^\circ}{T_{\mathrm{F}}}-\frac{360^\circ}{T_{\mathrm{M}}}=\frac{168{,}6^\circ}{\textrm{év}}, \)
így a legrövidebb várakozási idő:
\(\displaystyle t_1=\frac{\gamma}{\omega_{\mathrm{rel}}}=1{,}243~\textrm{év}\approx 454~\textrm{nap}. \)
Elekes Panni (Budapest-Fasori Evangélikus Gimn., 10. évf.)
Megjegyzések. 1. A megadott ellipszispályát Hohmann-pályának nevezik Walter Hohmann német mérnök után, aki 1925-ben javasolta, mint rakétaüzemanyag-felhasználás szempontjából leggazdaságosabb bolygóközi pályát.
2. A Mars és a Föld
\(\displaystyle T_{\mathrm{rel}}=\frac{360^\circ}{\omega_{\mathrm{rel}}}=2{,}135~\textrm{év}\approx 780~\mathrm{nap} \)
időközönként kerül ugyanilyen relatív helyzetbe, így az első lehetséges alkalom után ennyi időnként adódik újabb lehetőség a visszaindulásra.
3. A Föld és a Mars pályájának numerikus excentricitása: 0,0167, illetve 0,0934. A Mars-pálya inklinációja (a pálya síkjának a Föld pályájáéval, vagyis az ekliptikával bezárt szöge): \(\displaystyle 1{,}85^\circ\). Ezeket a végső, pontosabb tervezéskor figyelembe kell venni.
22 dolgozat érkezett. Helyes 8 megoldás. Kicsit hiányos (4 pont) 4, hiányos (2–3 pont) 10 dolgozat.
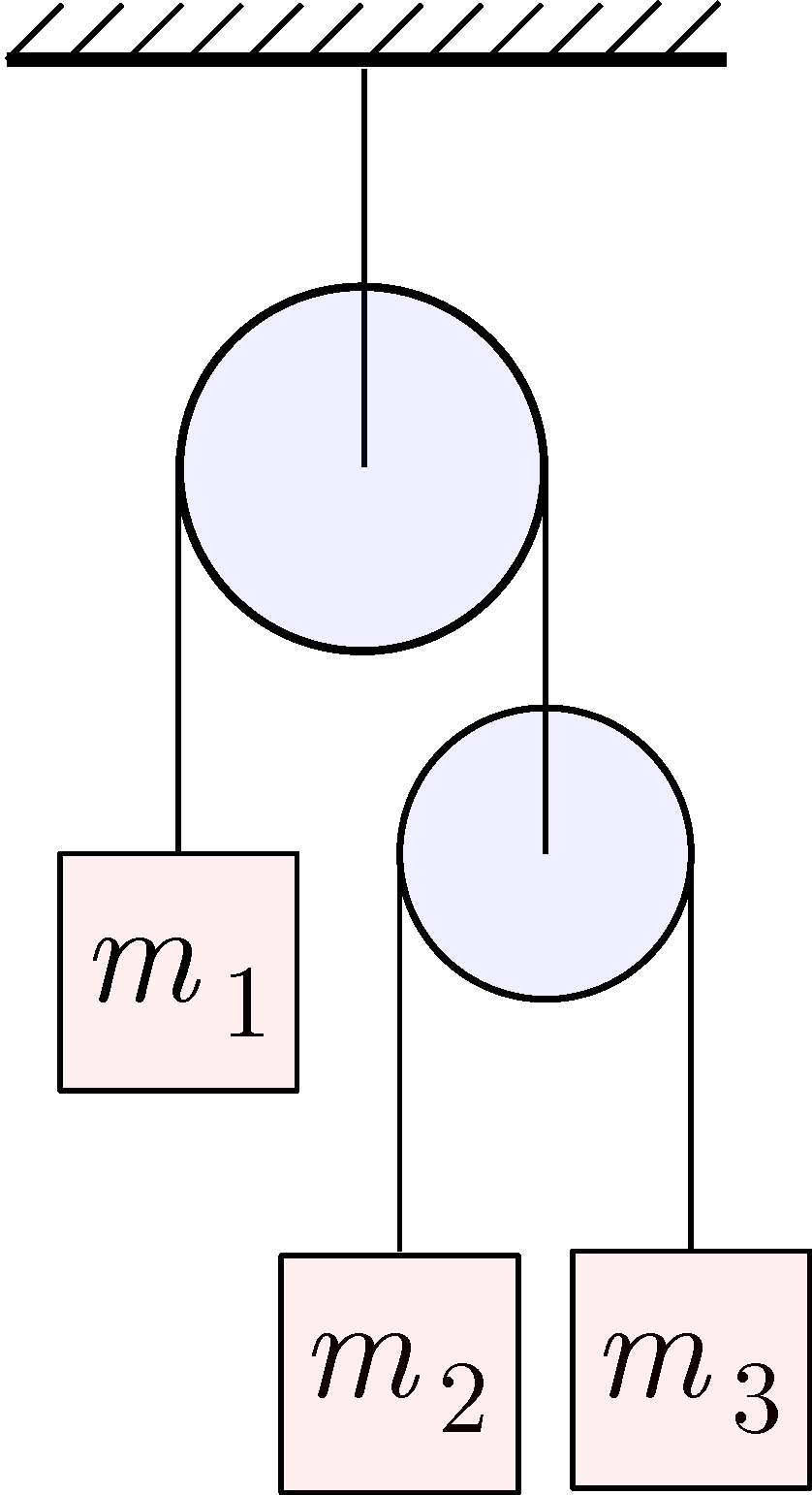
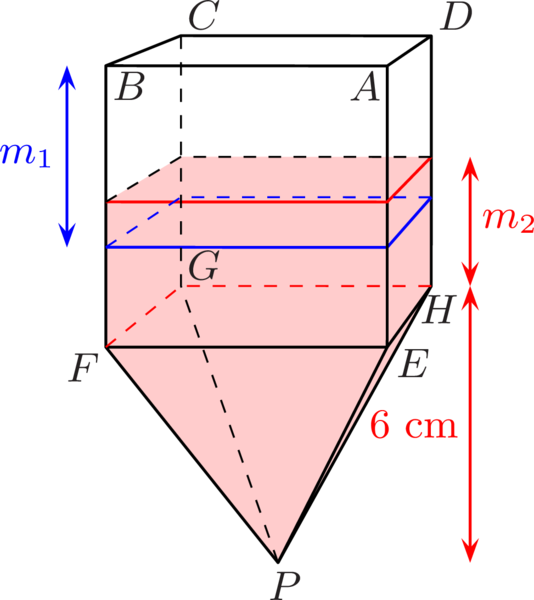
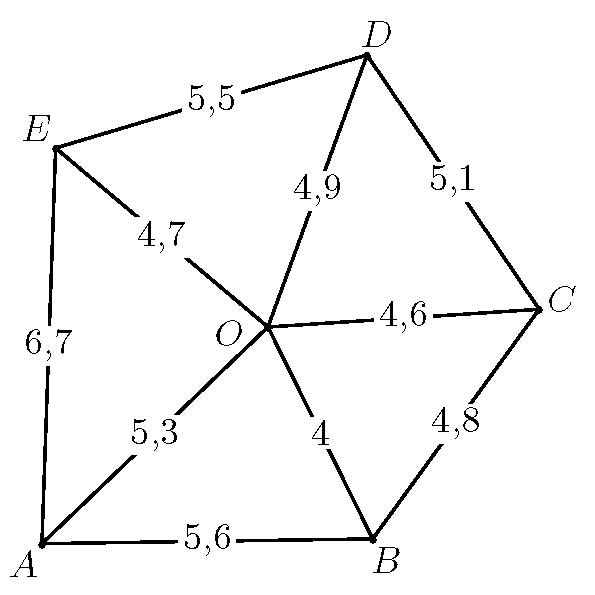
P. 5644. Milyen egyetlen, \(\displaystyle m\) tömeggel kellene helyettesíteni az ábrán szereplő jobb oldali csigát és a rajta lévő tömegeket, hogy az \(\displaystyle m_{1}\) tömegű test ugyanúgy mozogjon, mint az eredeti elrendezésben? Hanyagoljuk el a csigák tömegét és a súrlódást.
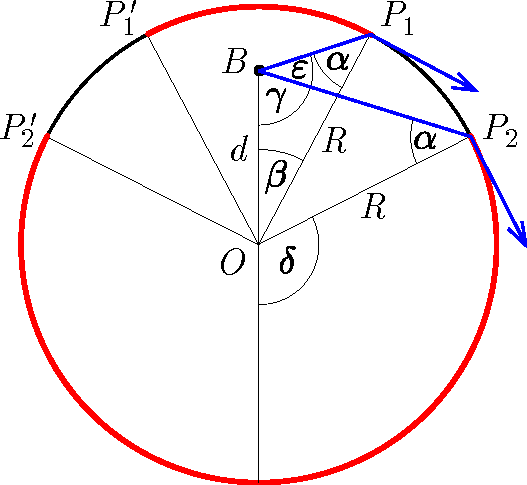
P. 5640. A Kanári-szigetek legnagyobb városában, Las Palmasban található egy Európában egyedülálló kiállítás, amely a Föld vizeinek élővilágát mutatja be. A kiállítás egyik attrakciója egy \(\displaystyle 400\) köbméteres, függőleges, henger alakú tengeri akvárium, melynek karbantartását búvárok végzik. Vízszintesen körbenézve az akvárium falának hányad részén lát ki az a búvár, aki az \(\displaystyle R\) sugarú henger szimmetriatengelyétől \(\displaystyle d\) távolságra van? A tengervíz törésmutatója \(\displaystyle n\).
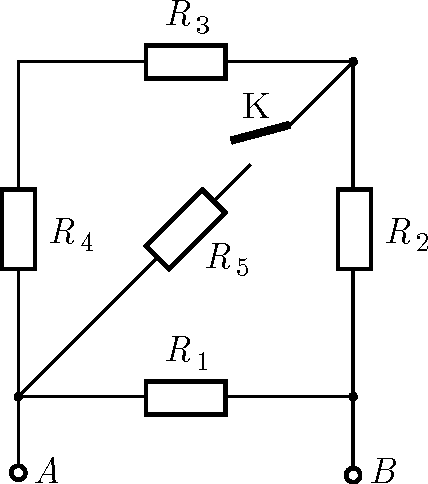
G. 896. Öt ellenállást kapcsolunk az ábra szerint egy 24 V-os feszültségforrás \(\displaystyle A\) és \(\displaystyle B\) kimenetére. Az ellenállások: \(\displaystyle R_1=40~\Omega\), \(\displaystyle R_2=50~\Omega\), \(\displaystyle R_3=R_4=10~\Omega\) és \(\displaystyle R_5=20~\Omega\).
a) Határozzuk meg az áramkör eredő ellenállását a kapcsoló zárt és nyitott állásában!
b) Mennyivel változik meg az \(\displaystyle R_4\) ellenállás teljesítménye, ha a zárt kapcsolót kinyitjuk?
(4 pont)
Közli: Veres Dénes, Szolnok
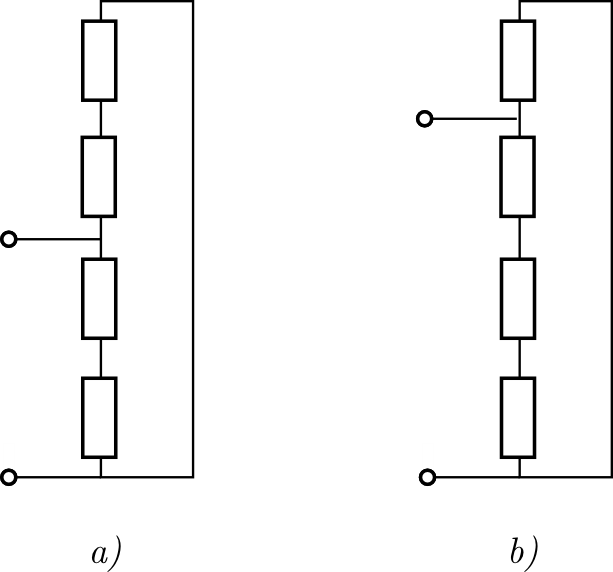
G. 900. Megválasztható-e az ábrán látható ohmos ellenállások (nullától különböző) nagysága úgy, hogy az eredő ellenállás az a) és b) esetekben egyenlő legyen?
de Châtel Péter (1940–2023) feladata nyomán
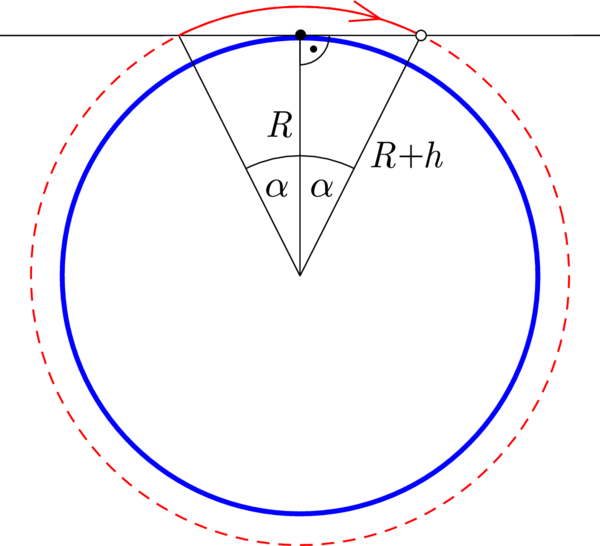
P. 5672. Az Egyenlítőn állva, éppen a fejünk felett halad át egy műhold, amely a Föld felszínétől \(\displaystyle 400~\mathrm{km}\)-re levő pályán kering. Legfeljebb mennyi ideig láthatjuk a műholdat?
Közli: Németh László, Fonyód
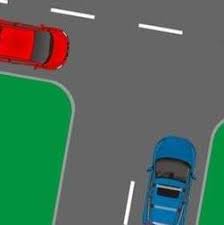
P. 5653. Két egyenes út merőlegesen keresztezi egymást. Az egyik úton egy személyautó \(\displaystyle 90~\mathrm{km}/\mathrm{h}\) sebességgel, a másikon egy motoros \(\displaystyle 72~\mathrm{km}/\mathrm{h}\) sebességgel közeledik a kereszteződéshez. Egy adott (\(\displaystyle t=0\)) pillanatban a két jármű távolsága (légvonalban) \(\displaystyle 347~\mathrm{m}\). \(\displaystyle 5\) másodperc elteltével a távolságuk \(\displaystyle 188~\mathrm{m}\)-re csökken.
a) Milyen messze volt a két jármű a kereszteződéstől kezdetben?
b) Mekkora lesz a két jármű közötti legkisebb távolság?
Az egyszerűség kedvéért mindkét járművet tekintsük pontszerűnek.
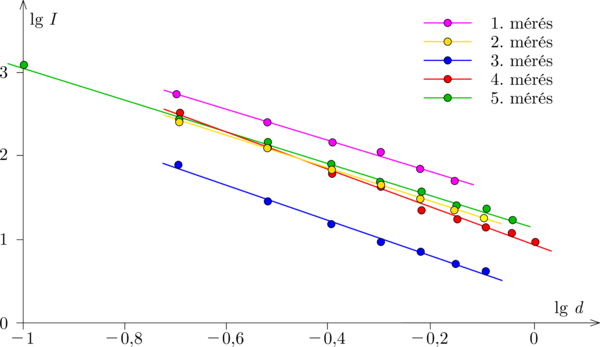
M. 443. Mobiltelefon fényérzékelőjét használva mutassuk meg, hogy a fényintenzitás inverz négyzetesen függ egy pontszerű fényforrástól mért távolságtól! Hogyan válasszuk a kísérleti körülményeket ahhoz, hogy minél pontosabban tudjuk igazolni ezt az összefüggést?
Közli: Vadász Gergely, Solymár
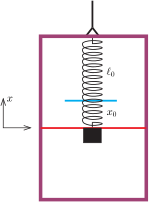
P. 5678. Egy \(\displaystyle D\) rugóállandójú rugó egyik végét egy lift mennyezetéhez rögzítjük, másik végére pedig egy \(\displaystyle m\) tömegű testet akasztunk. Kezdetben a test egyensúlyban van. Egyszer csak a lift állandó \(\displaystyle a\) gyorsulással elindul felfelé, majd \(\displaystyle \tau\) idő után a gyorsulás megszűnik és a felvonó állandó sebességgel halad tovább. Mekkora amplitúdójú mozgást végez ezután a test?
Közli: Vigh Máté, Herceghalom
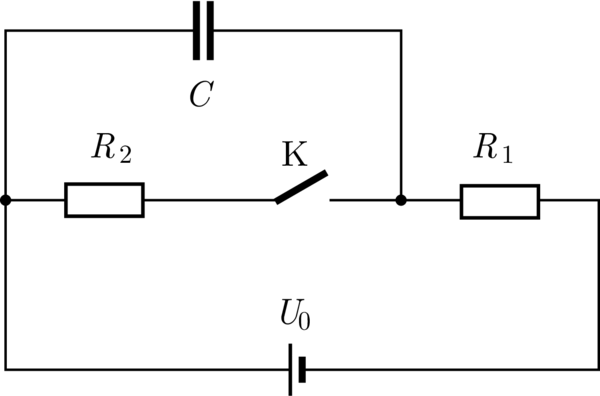
P. 5676. Az ábrán látható kapcsolási rajz szerint összeállított áramkörben szereplő feszültségforrás elektromotoros ereje \(\displaystyle 20~\mathrm{V}\), az ellenállások \(\displaystyle R_1=50~\Omega\), illetve \(\displaystyle R_2=150~\Omega\) nagyságúak, a kondenzátor \(\displaystyle 20~\mu\mathrm{F}\) kapacitású. Kezdetben a K kapcsoló zárva van.
a) Mekkora a kondenzátor töltése a kapcsoló zárt állása esetén?
b) A kapcsoló nyitását követően kialakuló állandósult állapot eléréséig mennyivel változik meg a kondenzátor energiája, és mennyi hő fejlődik az \(\displaystyle R_1\) ellenálláson?
A feszültségforrás belső ellenállása elhanyagolható.
Tornyai Sándor fizikaverseny, Hódmezővásárhely
P. 5660. Egy pontszerűnek tekinthető, \(\displaystyle m\) tömegű, átfúrt golyó az ábra szerint egy \(\displaystyle R\) sugarú, vízszintes átmérőjű, függőleges síkú, félkör alakú, rögzített, merev drótra van fűzve, amelyen súrlódásmentesen csúszhat. A golyóhoz egy vékony fonál van kötve, amely a drót \(\displaystyle C\) végén lévő, kicsiny csigán van átvetve. A fonál másik végéhez egy ugyancsak \(\displaystyle m\) tömegű nehezék van erősítve. A bal oldali golyót a fonál vízszintes helyzetéből lökésmentesen elengedjük, amikor a fonál \(\displaystyle \alpha=0^\circ\)-os szöget zár be a vízszintes átmérővel.
a) Mekkora sebességgel mozognak a testek, amikor a bal oldali test a drótpálya legalsó pontján halad át?
b) Mekkora a testek gyorsulása ebben a pillanatban?
Közli: Zsigri Ferenc, Budapest
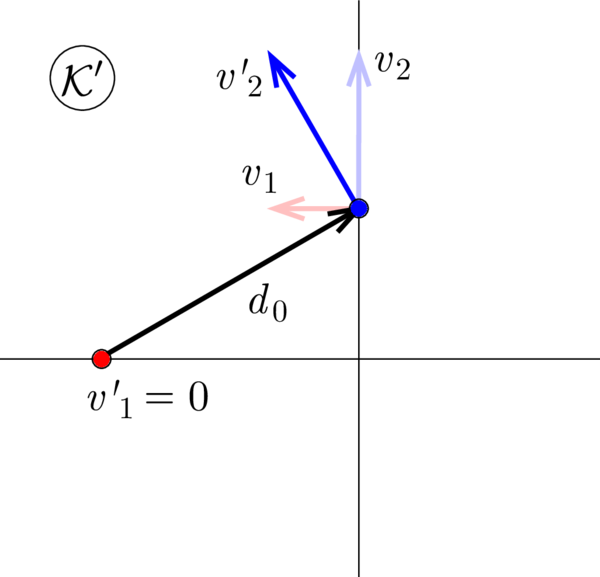
P. 5670. Két, egymást merőlegesen keresztező úton egy-egy motoros halad. Az egyik sebessége \(\displaystyle v_1\), a másiké \(\displaystyle v_2\), és az egymástól való legkisebb távolságuk \(\displaystyle d_0\). Milyen távolságra vannak ekkor a kereszteződéstől?
Közli: Woynarovich Ferenc, Budapest
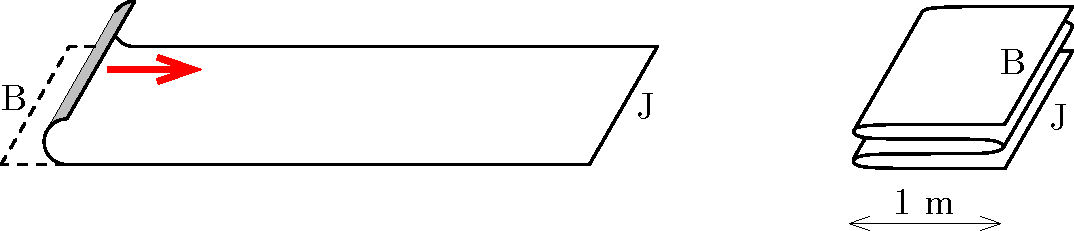
G. 893. A folyosó padlójára leterített, \(\displaystyle 4~\mathrm{m}\) hosszúságú szőnyeget négyrét (négy egyforma rétegben) összehajtjuk úgy, hogy bal oldali szegélyét (B) megfogjuk, és folyamatosan \(\displaystyle 20~\mathrm{cm}/\mathrm{s}\) nagyságú, vízszintes irányú sebességgel először jobbra, azután balra, majd ismét jobbra visszük. (Lásd az ábrát!)
a) Mennyi időt vesz igénybe a szőnyeg összehajtása?
b) Az összehajtás megkezdésétől mért \(\displaystyle 5~\mathrm{s}\) elteltével a szőnyegnek milyen hosszú darabja rendelkezik jobbra irányuló sebességgel? A szőnyeg vékony, könnyen hajtható anyagból készült, és nem csúszik meg a padlón. Az irányváltoztatások pillanatszerűen következnek be.
ELTE
Az ELTE-n végzett matematikusokat nemcsak a kutatóintézetek, egyetemek várják, hanem számos cég is, igen jó fizetéssel. Esetleg még nem döntöttél, de leginkább matematikából folytatnál felsőfokú tanulmányokat? Minderre kitűnő lehetőség nyílik az ország egyik legnagyobb múltú egyetemén, az Eötvös Loránd Tudományegyetem Természettudományi Karán, ahol világhírű professzoroktól és lelkes, közvetlen fiatal oktatóktól tanulhatsz. Pezsgő diákélet vár rád az ELTE korszerű számítógépparkkal felszerelt, a KöMaL szerkesztőségének is otthont adó modern lágymányosi épületegyüttesében.
Az ELTE TTK Fizikai és Csillagászati Intézetében a kíváncsiságból kutatás, az ötletekből felfedezés, a tanulásból pedig valódi lehetőség lesz. Magyarországon a fizika területén az ELTE áll az első helyen, a nemzetközi ARWU rangsorban pedig a 201–300. helyezés közé tartozik a fizika szakterületén – vagyis nemzetközi mércével nézve is erős helyen tanulhatsz.
A hat féléves fizika alapképzés közös törzsszakaszra épül, ahol stabil matematikai, fizikai, informatikai és elektronikai alapokat szerzel. A harmadik félévtől specializációt választhatsz az érdeklődésed szerint: fizikus, informatikus fizikus, biofizikus, csillagász, geofizikus vagy meteorológus.
A 2025/26-os tanévi fizika diákolimpiai válogatóverseny első fordulója 2026. február 24-én, kedden 15 órakor kezdődik online formában. A versenyre nevezni előzetesen nem kell, bárki részt vehet rajta. A feladatsor az ipho.physics.bme.hu oldalon lesz elérhető.
Fleiner Tamás
A Bolyai János Matematikai Társulat a 2025. évi Kürschák József Matematikai Tanulóversenyt október 10-én, közép-európai idő szerint 14 órai kezdettel rendezte meg a következő tizenhárom helyszínen: Budapest, Cambridge, Csíkszereda, Debrecen, Eger, Győr, Gyula, Ithaca, Kolozsvár, Miskolc, Szeged, Székesfehérvár és Veszprém.
A Társulat elnöksége a verseny lebonyolítására az alábbi bizottságot kérte fel: Biró András, Fleiner Tamás (elnök), Frenkel Péter, Harangi Viktor, Kós Géza, Kovács Benedek (titkár), Maga Péter, Pach Péter Pál és Tóth Géza. A bizottság szeptember 10-i ülésén az alábbi feladatokat tűzte ki:
Széchenyi Gábor, Vankó Péter, Vigh Máté, Vladár Károly
Az Eötvös Loránd Fizikai Társulat 2025. évi Eötvös-versenye október 17-én délután 3 órai kezdettel tíz magyarországi helyszínen került megrendezésre. Az ünnepélyes eredményhirdetésre és díjkiosztásra 2025. november 28-án délután került sor az ELTE TTK Eötvös termében. Megemlékeztünk az 50 és 25 évvel ezelőtti Eötvös-versenyről, ismertettük az akkori feladatokat és a győztesek nevét. Az 50 évvel ezelőtti díjazottak közül Virosztek Attila, a 25 évvel ezelőttiek közül Pozsgay Balázs volt jelen – ők röviden beszéltek a versennyel kapcsolatos emlékeikről és a pályafutásukról. Az 50 évvel ezelőtti II. díjas Zimányi Gergely videóüdvözletet, a 25 évvel ezelőtti I. díjas Buruzs Ádám pedig szöveges üzenetet küldött a jelenlévőknek.
Rövid betegség után elhunyt Holics László tanár úr, az ELTE Apáczai Csere János Gyakorlóiskola tanára, a KöMaL szerkesztője, több, mint 500 KöMaL fizika feladat szerzője.
25. alkalommal adták át a Rátz Tanár úr életműdíjakat összesen nyolc kiváló tanár részére:
Kántor Sándorné, Dr. Pintér Klára, Ábrám László, Horváth Norbert, Karasz Gyöngyi, Nagy István, Bódis Bertalan, Mándics Dezső.
A kitüntetettek részletes bemutatása és az évente megújuló felhívás megtalálható a Rátz Tanár Úr Életműdíj hivatalos honlapján: https://www.ratztanarurdij.hu/
Kozma Katalin Abigél
Idén Miskolc vendégül a matematikatanárok csapatát a Rátz László Vándorgyűlés keretei között. Négy szekcióban zajlottak a szemináriumok és az előadások, ezen kívül átadták a Bolyai János Matematikai Társulat Beke Manó Emlékdíjait és a Reményi díjakat az országos matematikaversenyeken kiváló eredményt elért tanulók tanárainak.
Idén 2025. június 12-én az Ericsson Magyarország székházában adták át az Ericsson díjakat. Hat kategóriában összesen kilenc pedagógus nyerte el a rangos elismerést és a vele járó \(\displaystyle 500\;000\) Ft-os jutalmat.
Az ünnepélyes díjátadón immár 25. alkalommal nyújtottak át ilyen díjakat a középiskolai matematika- és fizikaoktatás kiemelkedő pedagógusainak, míg a „Digitális kultúra népszerűsítéséért” és a „Digitális kultúra tehetségeinek gondozásáért” díjak átadására idén másodszor került sor.
