Beszámoló a 9. Európai Fizikai Diákolimpiáról
Szász Krisztián, Vankó Péter
Idén 2025. június 13. és 17. között Szófiában, Bulgária fővárosában rendezték meg az Európai Fizikai Diákolimpiát (EuPhO). A versenyen 29 európai és 10 Európán kívüli ország összesen 194 diákja vett részt, közülük 130 diák kapott érmet vagy dicséretet. A magyar csapat tagjai egy ezüst- és három bronzérmet szereztek.
A Nemzetközi Fizikai Diákolimpiára (IPhO) és az EuPhO-ra a felkészülés a szokásos módon szeptemberben kezdődött: ebben a tanévben már az ország hat városában (Budapesten, Debrecenben, Miskolcon, Pécsett, Szegeden és Székesfehérváron) működött olimpiai szakkör. A jelenléti szakkörökön kívül továbbra is elérhetők az IPhO Hungary YouTube-csatorna és a szakköri honlapra felkerülő feladatsorok. A válogatás február végén egy online formában megrendezett fordulóval kezdődött, amelyen bárki részt vehetett. Összesen harmincketten küldtek be dolgozatot, közülük tizenegy diák kapott meghívást a további fordulókra. A válogatás online felkészítéssel és négy villámversennyel folytatódott, majd a BME Fizikai Intézetében megrendezésre kerülő kétnapos döntővel zárult, ahol az elméleti feladatok mellett egy olimpiai stílusú mérési feladatot is meg kellett oldania a versenyzőknek. A felkészítések és a versenyek szervezésében Barankai Norbert, Berke Martin, Sarkadi Tamás, Szász Krisztián, Széchenyi Gábor, Tasnádi Tamás, Vankó Péter és Vigh Máté vett részt. A kiválasztott csapat (mindkét olimpiára):
Bencz Benedek (Baár-Madas Református Gimnázium, Általános Iskola és Diákotthon, 12. oszt.), felkészítő tanára: Horváth Norbert;
Elekes Dorottya (Budapest-Fasori Evangélikus Gimnázium, 12. oszt.), felkészítő tanára: Izsa Éva;
Erdélyi Dominik (Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium, 11. oszt.), felkészítő tanárai: Nagy Piroska Mária és Schramek Anikó;
Téti Miklós (Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium, 11. oszt.), felkészítő tanára: Schramek Anikó;
Tóth Kolos Barnabás (Eötvös József Gimnázium, 11. oszt.), felkészítő tanára: Varga Balázs.
A csapatnak június elején a BME Fizikai Intézetében kétnapos felkészítést tartottunk, ahol elsősorban mérési feladatok elvégzésére és megbeszélésére volt lehetőség. A válogatóverseny és a felkészítés szállás- és étkezési költségeire a MATFUND Alapítvány biztosított támogatást.
A csapat 2025. június 13-án repülővel utazott Szófiába, ahol aznap este már az olimpia megnyitója volt. A mérési és elméleti fordulókat június 14-én és 15-én rendezték meg. A versenyen kívül a diákoknak városnéző sétákat szerveztek. A moderációra (a megoldásokért járó végleges pontszám megvitatása, amely ezen a versenyen az IPhO-val szemben a diákok feladata) június 16-án volt lehetőség, és ezen a napon volt a búcsúvacsora is. Az eredményhirdetésre másnap, június 17-én délelőtt került sor, ezzel zárult a hivatalos program. A magyar csapat ezután egy tradicionális bolgár étteremben ebédelt, majd este repülővel utazott haza.
A versenyen maximálisan 50 pontot lehetett szerezni. A legjobb eredményt Marián Kovaľ, Szlovákia érte el (40,3 pont). A versenyen 18 aranyérmet (29,8 ponttól), 38 ezüstérmet (19,3 ponttól), 44 bronzérmet (13,0 ponttól) és 30 dicséretet (9,4 ponttól) osztottak ki. A legjobb mérésért járó különdíjat egy román, a legjobb elméletért járót egy német diák kapta. A nem hivatalos éremtáblázat élén Észtország végzett három arany-, valamint egy-egy ezüst- és bronzéremmel. A magyar csapat tagjainak eredményei:
Téti Miklós 19,4 pont, ezüstérem;
Elekes Dorottya 18,7 pont, bronzérem;
Bencz Benedek 16,9 pont, bronzérem;
Tóth Kolos Barnabás 14,3 pont, bronzérem;
Erdélyi Dominik 4,7 pont.
A csapat vezetői Szász Krisztián és Vankó Péter voltak.
Az alábbiakban közöljük a verseny feladatait (a mérés szövegét kicsit rövidítve), a megoldások (és a mérés teljes szövege) a verseny honlapján érhetők el: https://eupho.ee/eupho-2025/.
Az EuPhO-n való részvételt a Nemzeti Tehetség Program támogatta az NTP-NTMV-24-B-0003 számú pályázat keretében.
Elméleti feladatok
T1 – Napos (10 pont)
Tanulmányozd a fényes köröket és a sötét gyűrűket az alábbi ábrákon! Számításaidat a következő idealizált körülmények feltételezésével végezd: a székláb egy pontosan függőleges, \(\displaystyle a\) sugarú henger, tökéletesen sima, hengeres és tökéletesen fényvisszaverő felülettel. Használhatsz további észszerű feltételezéseket és közelítéseket is, ha azok egyszerűsítik a számításaidat.
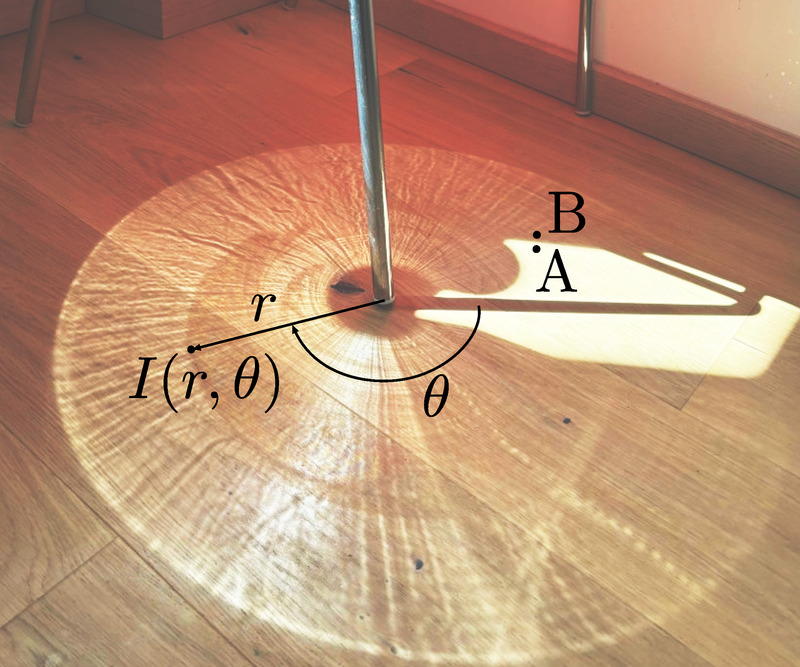
1. ábra
a) Határozd meg, hogy a fényesen megvilágított körön belül a padlón lévő \(\displaystyle I(r,\theta)\) megvilágítási többlet hogyan függ az \(\displaystyle r\gg a\) és \(\displaystyle \theta\) polárkoordinátáktól! A megvilágítás a beérkező fény mennyiségét adja meg területegységenként. ,,Többlet'' alatt a henger jelenléte miatt keletkező járulékos megvilágítást értjük. Az eredményt az 1. ábra A és B pontjai közötti \(\displaystyle I_0\) megvilágítási különbség segítségével fejezd ki. (5 pont)
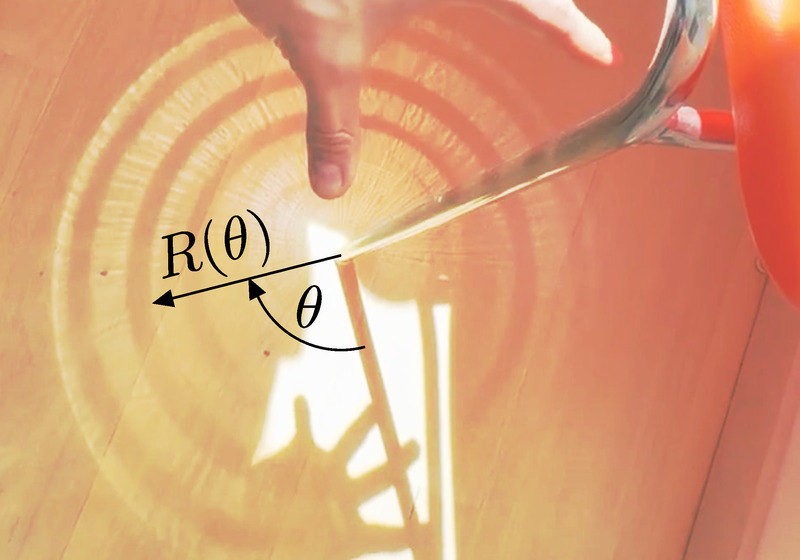
2. ábra
b) A 2. ábrán néhány ujj kitakarja a széklábat elérő fény egy részét. Jelölje \(\displaystyle R(\theta)\) a középső sötét gyűrű radiális távolságát a \(\displaystyle \theta\) szög függvényében, és legyen \(\displaystyle R_{\textrm{min}}\) az \(\displaystyle R(\theta)\) minimális értéke. Határozd meg az \(\displaystyle R(\theta)-R_\textrm{min}\) függvényt! (5 pont)
T2 – Lebegő asztal (10 pont)
Egy asztal úgy készült, hogy egy fémkeretet egy nehéz, homogén laphoz rögzítenek (így merev testet alkotnak), és láncokkal egy másik, vízszintes talajra rögzített kerethez erősítik. Az asztal mozgását az oldalnézeti síkban vizsgáljuk (a 3. ábra jobb oldalán).
a) Mutasd meg, hogy az ábrázolt helyzetben az asztal stabil egyensúlyban van! (4 pont)
b) Határozd meg a kis rezgések \(\displaystyle T\) periódusidejét! (6 pont)
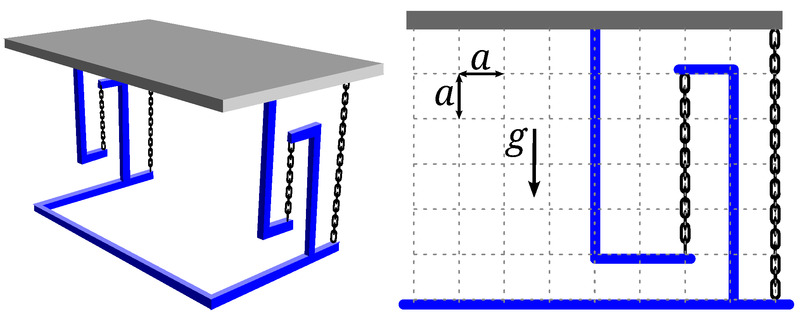
3. ábra
A láncok és a keret tömege elhanyagolható. A láncok súrlódásmentesek, nyújthatatlanok és rezgés közben is feszesek maradnak. A rácsháló mérete \(\displaystyle a=0{,}100~\mathrm{m}\), a nehézségi gyorsulás \(\displaystyle g=9{,}81~\mathrm{m/s^2}\).
T3 – Keresztezett vezetékek (10 pont)
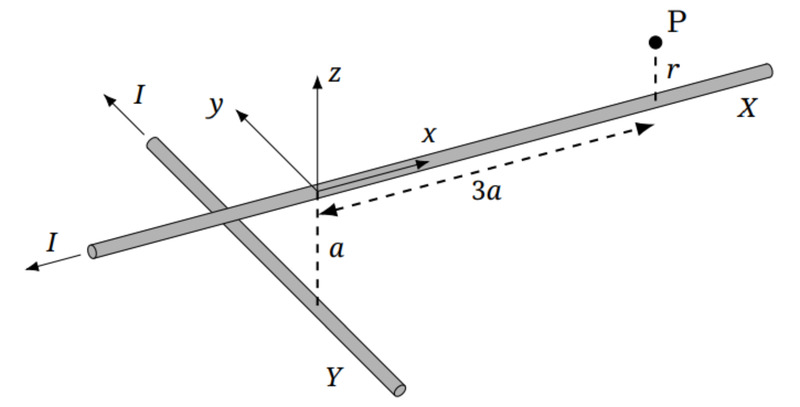
4. ábra
a) Egy végtelen, egyenes, vékony huzalon áram folyik. A huzallal párhuzamosan egy külső, homogén mágneses mezőt kapcsolunk be. Vázlatosan rajzolj fel egy mágneses erővonalat! (1 pont)
b) Most tekintsük a 4. ábrán látható két, végtelen, egyenes, vékony vezetéket (\(\displaystyle X\) és \(\displaystyle Y\)), amelyek mindegyikében \(\displaystyle I\) áram folyik. Az \(\displaystyle x\) tengely egybeesik az \(\displaystyle X\) huzallal, míg az \(\displaystyle Y\) huzal párhuzamos az \(\displaystyle y\) tengellyel, és áthalad a \(\displaystyle (0,0,-a)\) ponton. Legyen P a \(\displaystyle (3a,0,r)\) pont. Feltételezve, hogy \(\displaystyle {r\ll a}\), számítsd ki a P-n áthaladó mágneses erővonal \(\displaystyle X\) huzaltól mért legkisebb \(\displaystyle d\) távolságát! (5 pont)
c) Legyen ennek az erővonalnak a \(\displaystyle P\) pont és az erővonal \(\displaystyle X\) vezetékhez legközelebb eső pontja közötti hossza \(\displaystyle L\). Az \(\displaystyle a=10~\mathrm{cm}\) és \(\displaystyle r=1{,}0~\mathrm{mm}\) értékek felhasználásával számítsd ki \(\displaystyle L\) értékét \(\displaystyle 20\%\) relatív hibahatáron belül! (4 pont)
Kísérleti feladatok
E1 – Deep learning (10 pont)
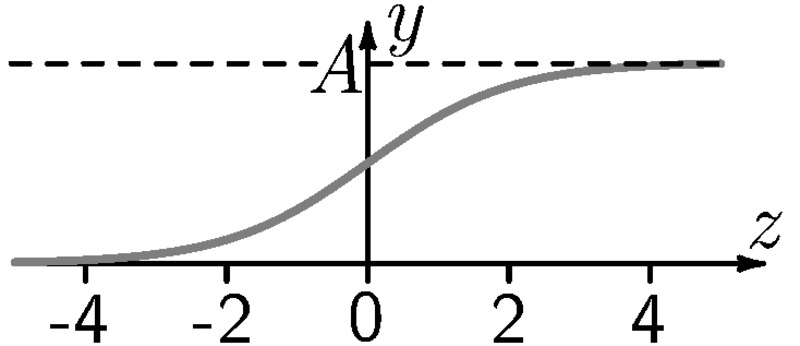
5. ábra
A modern mesterséges neurális hálózatok (ANN) több milliárd neuronból állnak. Minden egyes neuron az \(\displaystyle x_1,x_2,\ldots,x_n\) bemenet(ek)et egy \(\displaystyle y\) kimenetté alakítja. Először a
\(\displaystyle z=w_1x_1+w_2x_2+\dots+w_n x_n+b \)
kerül kiszámításra valós \(\displaystyle w_i\) súlyok és valós ún. \(\displaystyle b\) bias értékekkel. Ezután egy aktiváló függvényt alkalmazunk \(\displaystyle z\)-re a végső \(\displaystyle y(x_1,x_2,\dots)\) kimenet előállításához. A jelen feladatban egy neuron fizikai modelljét vizsgáljuk, amelynek bemenetei az \(\displaystyle x_1\) és \(\displaystyle x_2\) elektromos feszültségek, az aktiváló függvény pedig az 5. ábrán látható \(\displaystyle A\sigma(z)\), ahol \(\displaystyle \sigma(z)=1/(1+\exp(-z) )\) az úgynevezett szigmoid függvény.
Eszközök (Fontos: Tápegységet ne kapcsolj ki!)

6. ábra
(i) Egy doboz, amely egy feszültségforrást, egy neuront modellező elektronikus áramkört és két potenciométert (az A-potenciométert és a B-potenciométert) tartalmaz (6. ábra). A doboz elektromos csatlakozóit a következőképpen jelöljük:
Két, elektromosan összekapcsolt GND-csatlakozás: a +V, \(\displaystyle x_1\), \(\displaystyle x_2\) és \(\displaystyle y\) közös negatív pólusaként szolgáló elektromos föld.
\(\displaystyle +{}\)V: a feszültségforrás pozitív pólusa.
X1 és X2: a neuronok \(\displaystyle x_1\) és \(\displaystyle x_2\) bemeneti feszültségeinek pozitív termináljai. A neuron kimenete nem kiszámíthatóan viselkedik, ha e két terminál valamelyikén nincs bemeneti feszültség.
Y: a pozitív kimeneti csatlakozó. Úgy viselkedik, mint egy valós feszültségforrás, amely egy \(\displaystyle y\) feszültségű ideális feszültségforrásból és egy \(\displaystyle R_\mathrm{out}\) soros kimeneti ellenállásból áll, és a 7. ábrán látható módon működik.

7. ábra
A1, A2, A3: az A potenciométer csatlakozói.
B1, B2, B3: a B potenciométer csatlakozói.
T: a feladatban nem használt kivezetés.
(ii) Digitális multiméter két vezetékkel.
(iii) Banáncsatlakozóval ellátott vezetékek.
(iv) Milliméterpapír.
E1.1 (0,5 pont)
Az A1, A2 és A3 terminálok az \(\displaystyle R_P\) A potenciométerhez és egy további \(\displaystyle R_L\) terhelő ellenálláshoz csatlakoznak.
A 8. ábrán melyik rajz felel meg a dobozban lévő áramkörnek? Határozd meg az \(\displaystyle R_L\) és \(\displaystyle R_P\) ellenállásokat!

8. ábra
Megjegyzés: A B potenciométert a B1, B2, B3 csatlakozókhoz pontosan ugyanúgy kell csatlakoztatni, ugyanazokkal (a gyártási tűréshatáron belül) az \(\displaystyle R_L\) és \(\displaystyle R_P\) ellenállásokkal.
E1.2 (0,5 pont)
Vázold fel, hogyan kell a csatlakozókat összekötni, hogy a neuronok bemeneti feszültségei a lehető legszélesebb tartományban változtathatók legyenek!
E1.3 (1,5 pont)
Dolgozz ki egy olyan eljárást, amely lehetővé teszi, hogy megtaláljuk az \(\displaystyle x_1\) és \(\displaystyle x_2\) bemeneti feszültségek olyan kombinációját, amely a lehető legkevesebb méréssel maximalizálja az \(\displaystyle y\) kimeneti feszültséget, függetlenül attól, hogy a keresést a bemeneti feszültségek milyen értékeivel kezdjük! Határozd meg ezt a maximális \(\displaystyle y_\mathrm{max}\) feszültséget, amelyet a továbbiakban az \(\displaystyle A\) amplitúdó közelítéseként fogsz használni.
E1.4 (3,5 pont)
Határozd meg a \(\displaystyle w_1, w_2\) súlyokat és a \(\displaystyle b\) értékét. Írd le a mérést, és add meg az adatokat táblázatban. Becsüld meg \(\displaystyle w_1, w_2\) és \(\displaystyle b\) értékét grafikus módszerrel!
A Training a hálózat súlyainak optimalizálását jelenti a kívánt hatékonyság elérése érdekében. Ez lehetővé teszi, hogy az ANN-ek tetszőleges függvényeket közelítsenek. Az alábbi feladatok mindegyikénél egy-egy bemeneti feszültség különböző függvényét kell közelítened a megadott eszközökkel. Ügyelj arra, hogy az áramkörökben egyértelműen jelöld az általad meghatározott bemenetet és kimenetet.
E1.5 (1,5 pont)
Csatlakoztasd az X1-et közvetlenül a +V-hez. Tervezz meg egy áramkört az \(\displaystyle y_5(x)=A\sigma\left(w_2x/2+b_5\right)\) függvény közelítésére, ahol \(\displaystyle x\) az újonnan definiált bemeneti csatlakozóra adott feszültség. Határozd meg \(\displaystyle b_5\)-öt elméleti úton. Építsd meg az áramkört, végezz méréseket, és vizsgáld meg, hogy az elrendezésed az elvárásoknak megfelelően működik-e! Az adatokból ellenőrizd \(\displaystyle b_5\) értékét.
E1.6 (2,5 pont)
a) Határozd meg az Y csatlakozó belső soros \(\displaystyle R_\mathrm{out}\) kimeneti ellenállását!
b) Tervezz és valósíts meg egy áramkört az \(\displaystyle y_6(x)=A_6\cdot\sigma(w_2x+b)+B_6\) függvény közelítésére, ahol \(\displaystyle B_6=1{,}48~\mathrm{V}\). Határozd meg elméletileg az \(\displaystyle A_6\) értékét. Építsd meg az áramkört, és vizsgáld meg kísérletileg, hogy a beállítás a várt módon működik-e! Az adataid alapján ellenőrizd az \(\displaystyle A_6\) és \(\displaystyle B_6\) értékeit.
E2 – Rejtett mintázatok (10 pont)
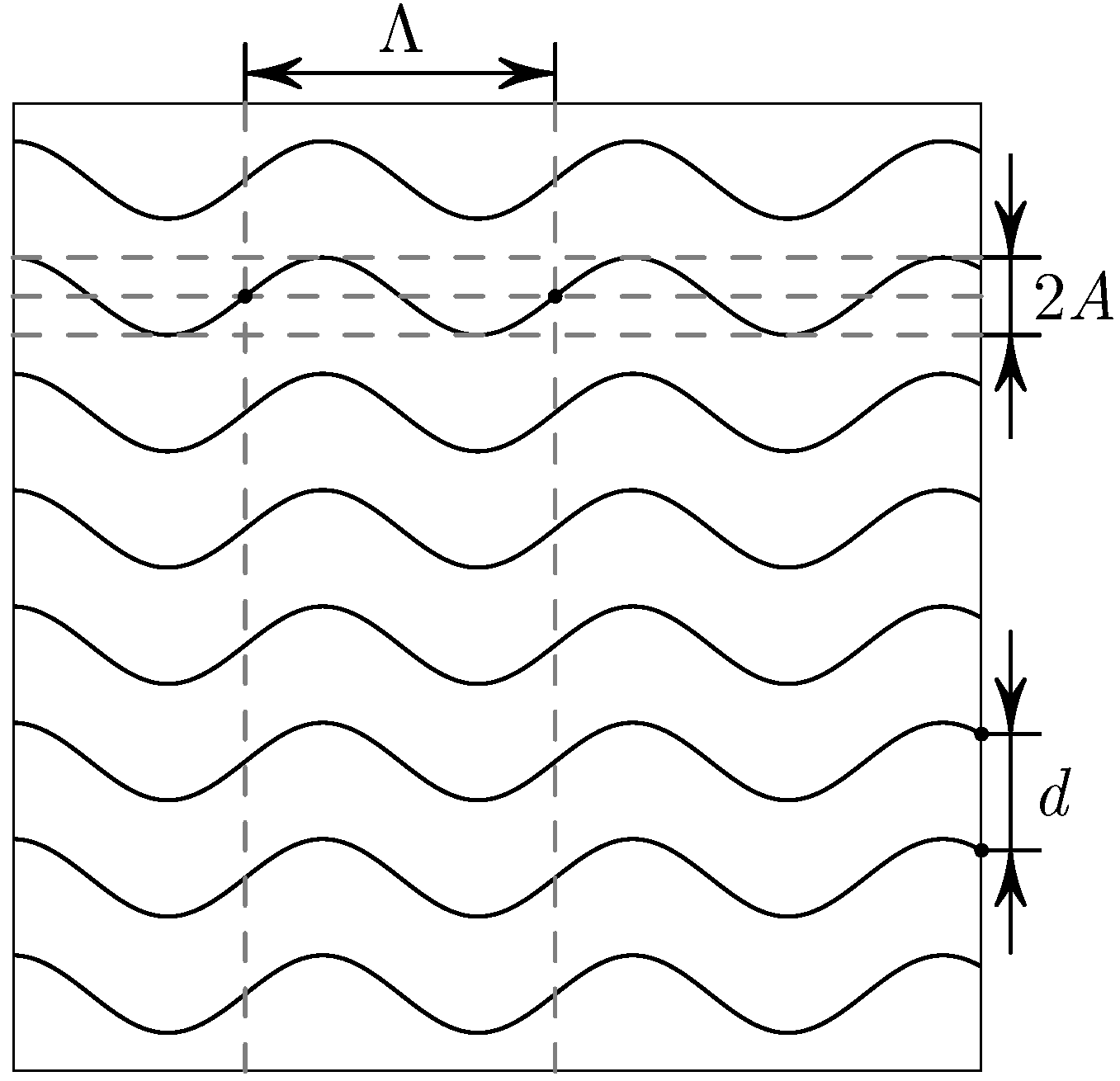
9. ábra
Rendelkezésedre áll egy félig átlátszó fólia, amelynek a felületére egy szabad szemmel nem látható mikromintázat van nyomtatva. A mintázat nagyszámú, egyforma, \(\displaystyle A\) amplitúdójú szinuszhullámból áll, amelyek vízszintes irányban \(\displaystyle \Lambda\) periódusúak, és függőleges irányban \(\displaystyle d\) távolsággal el vannak tolva egymástól, ahogy ezt vázlatosan a 9. ábra mutatja. Mikroszkóppal nézve a nyomtatott mintázat szigorúan vízszintes vonalszakaszokból áll, amelyek a szomszédjukhoz képest egy állandó \(\displaystyle s\) távolsággal függőlegesen el vannak tolva, ahogy ez a 10. ábrán látható.
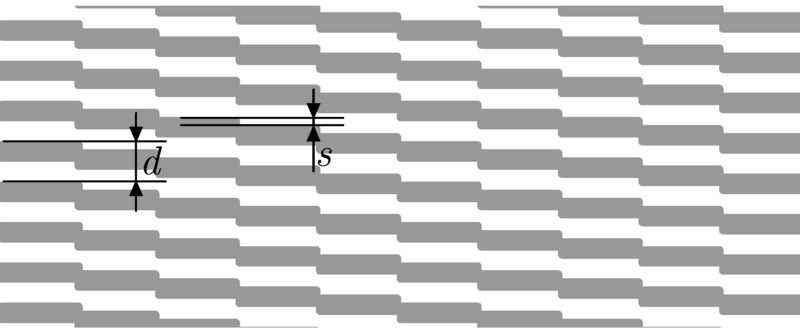
10. ábra A mintázat, ahogy egy mikroszkóp alatt látszik
Eszközök (lásd a 11. ábrát is)

11. ábra Az A, B, C, H és J elemek a méréshez elrendezve.
A Félig átlátszó fólia a felületére nyomtatott mikromintázattal.
B Lézerdióda \(\displaystyle \lambda\!=\!(654\pm 5)~\mathrm{nm}\) hullámhosszal. A lézerdiódát a zárókupak (amelyben egy lencse van) forgatásával a kívánt távolságra lehet fókuszálni.
C Két 90 fokos, L-alakú acéltartó a fóliának és a lézernek. A fóliát a kis csipesszel lehet az egyikhez rögzíteni, a lézerdiódát pedig a nagyobb, színes csipesszel vagy a befőttes gumival a másikhoz.
D Egy papírlapra nyomtatott szögmérő – egy polárkoordináta-rendszer sugárirányban 1 mm-es lépésekkel és fokonkénti szögbeosztással.
E Egy ernyő: az eszközöket tartalmazó doboz nagy felülete. Ürítsd ki a dobozt, és tedd úgy az asztalra, hogy a nagy felülete legyen függőleges.
F Vonalzó.
G Mérőszalag.
H Ragasztószalag a vonalzóra ragasztva. Használj belőle kis darabokat a szögmérő ernyőre való rögzítéséhez és az elemek asztalon való rögzítéséhez.
I Milliméterpapír.
J Egy 80 mm-es, átlós referenciavonalakkal ellátott papír, amely lehetővé teszi a fő skálabeosztások töredékeinek mérését \(\displaystyle \pm 0{,}1~\mathrm{mm}\) pontossággal.
Határozd meg a lehető legpontosabban:
a) a szinuszhullám \(\displaystyle \Lambda\) periódusát; (2 pont)
b) a szomszédos szinuszok \(\displaystyle d\) függőleges távolságát; (2 pont)
c) a szinusz \(\displaystyle A\) amplitúdóját; (3 pont)
d) az \(\displaystyle s\) lépcsőmagasságot! (3 pont)
Minden feladatnál elvárás, hogy vázold fel a mérési elrendezést és/vagy indokold meg az adott mennyiség mérési módszerét; táblázatos formában foglald össze a mérési adatokat és a számításokat; ahol lehet, határozd meg a keresett mennyiségeket és azok hibáját grafikusan.
*
Az idei IPhO-ról lapunk októberi számában jelenik meg beszámoló.
2026-ban az EuPhO Göteborgban (Svédország), az IPhO a kolumbiai Bucaramangában lesz. A versenyekre a felkészülés a szokásos módon 2025 szeptemberében kezdődik. A szakkörök helyéről, a szakkörvezetők elérhetőségéről és a foglalkozások időpontjáról a fizika diákolimpiai szakkörök hivatalos honlapján lehet tájékozódni:
A szakkörökön kívül önálló munkával, a KöMaL elméleti és mérési feladatainak rendszeres megoldásával lehet készülni a jövő évi versenyekre.
Eredményes felkészülést kívánunk!

