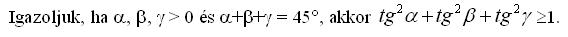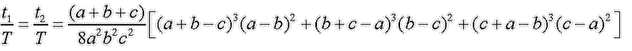Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány
Már regisztráltál?
Új vendég vagy?

Fórum: GEOMETRIA

  [1]    [2]    [3]    [4]    [5]    [6]    [7]    [8]    [9]    [10]    [11]    [12]    [13]    [14]    [15]    [16]    [17]    [18]    [19]    [20]    [21]    [22]    [23]    [24]    [25]    [26]    [27]    [28]    [29]    [30]    [31]    [32]    [33]    [34]    [35]    [36]    [37]    [38]    [39]    [40]    [41]    [42]    [43]    [44]    [45]    [46]    [47]    [48]    [49]    [50]    [51]    [52]    [53]    [54]    [55]    [56]    [57]    [58]    [59]    [60]    [61]    [62]    [63]    [64]    [65]    [66]    [67]    [68]    [69]    [70]    [71]    [72]    [73]    [74]    [75]    [76]    [77]    [78]  

Szeretnél hozzászólni? Jelentkezz be.
[1371] laci7772010-02-20 14:53:13

Köszönöm szépen - így leírva egyszerűnek tűnik. De nem állítanám, hogy térlátás nélkül evidens számomra a szögszár P pont körül elforgatása:(

Még egyszer köszönöm, kellemes hétvégét, szia: Laci

Előzmény: [1370] jenei.attila, 2010-02-20 14:38:03
[1370] jenei.attila2010-02-20 14:38:03

Legyen A és B a háromszög másik két csúcsa, amelyek az egyik illetve másik szögszárra esnek. Mivel a háromszög szabályos, ezért az A-t a B-be egy 60 fokos P középpontú forgatás viszi. Tehát forgasd el P körül az egyik szögszárat 60 fokkal, és ahol az elfogatott szögszár elmetszi a másik szögszárat, ott lesz az egyik keresett csúcs. Ezt visszaforgatva, megkapod a másik csúcsot.

Előzmény: [1369] laci777, 2010-02-20 14:00:57
[1369] laci7772010-02-20 14:00:57

Sziasztok!

Tudna valaki segíteni?

Egy geometria szorgalmi feladattal gyűlt meg a bajom:

Vegyünk egy 60 fokos szöget, és a szögszáron belül egy tetszőleges P pontot, ahogy a P nem illeszkedik a 60 fokos szöget felező félegyenesre.

A feladat: szerkesszünk olyan szabályos 3-szöget, amelynek a P pont az egyik csúcsa, a másik két csúcs pedig a 2 szögszáron található (száranként 1-1).

Bármilyen segítséget előre is köszönök szépen.

Kellemes hétvégét kívánok mindenkinek!

Sziasztok: Laci

[1368] HoA2010-01-14 11:45:29

Elnézést, én sem gondoltam egészen végig. A 3 adott kör közül kettőnek az érintési pontjára vonatkozó inverzió igen egyszerű megoldást ad: két párhuzamos egyenest és egy kört érintő kört kell szerkeszteni. A gyakorlati kivitelezés különösen egyszerű, ha a k1 és k2 érintési pontja mint középpont körül az inverzió alapkörét úgy vesszük fel, hogy merőlegesen metssze k3-at. Ekkor k3 képe önmaga, és így a k3-at és az őt érintő két párhuzamost érintő kört kell szerkeszteni.

Előzmény: [1363] S.Ákos, 2010-01-13 11:47:39
[1367] BohnerGéza2010-01-13 17:31:12

Egy megoldás a 163. feladatra és egy OKTV feladatra:

Előzmény: [1366] sakkmath, 2010-01-13 16:17:56
[1366] sakkmath2010-01-13 16:17:56

A 163. feladat bizonyítását a Matek OKTV [554]-es hozzászólásának végén olvashatjuk.

Előzmény: [1359] BohnerGéza, 2010-01-11 09:45:38
[1365] Bosnyak2010-01-13 16:01:02

Köszönöm a segítséget!!

Előzmény: [1364] HoA, 2010-01-13 12:06:17
[1364] HoA2010-01-13 12:06:17

Az apró trükk ott van, hogy a legegyszerűbb megoldás nem használja ki, hogy a körök érintik egymást: Csökkentsük a körök sugarát a legkisebbik - legyen k3 - sugarával, ekkor a szerkesztendő k4 körrel koncentrikus k5 kört kell szerkeszteni, ami a csökkentett sugarú k1' és k2' köröket érinti és átmegy az O3 ponton. Az O3 középpontú inverzióval ez két kör közös érintőjének szerkesztésébe megy át. A Geometriai feladatok gyűjteményében a két kört kívülről érintő, adott P ponton áthaladó kör szerkesztésére szerepel egy inverziót nem használó módszer. Ott a körök külső hasonlósági pontját P-vel összekötő egyenesnek azt a Q pontját határozzuk meg először, amely szintén rajta van a szerkesztendő körön és így visszavezetjük a feladatot a két ponton átmenő, adott kört érintő kör szerkesztésére.

Előzmény: [1362] Bosnyak, 2010-01-13 09:55:25
[1363] S.Ákos2010-01-13 11:47:39

Nem gondoltam teljesen végig, de az egyik érintési pontra vonatkozó inverzióval szerintem kijön.

Előzmény: [1362] Bosnyak, 2010-01-13 09:55:25
[1362] Bosnyak2010-01-13 09:55:25

Üdv mindenkinek! Volna egy problémám: Van három különböző tetszőleges sugarú kör ami érinti egymást. Annak a körnek a középpontját szeretném megszerkeszteni amely mind a három másik kört érinti,(belülről, a három kör által határolt területen) Remélem tud vki segíteni!

[1361] Cogito2010-01-12 11:31:57

Ez nem feltétel, csak loboncz megoldásában teljesülne, véletlenül.

Előzmény: [1360] gubanc, 2010-01-11 10:13:12
[1360] gubanc2010-01-11 10:13:12

És azt nem kell még kikötni, hogy mindegyik szög kisebb, mint 45°?

Előzmény: [1359] BohnerGéza, 2010-01-11 09:45:38
[1359] BohnerGéza2010-01-11 09:45:38

Két javítás:

Az előző hozzászólásban a 163. feladat van.

A szögek összege 45 fok helyett 90 fok!

Előzmény: [1358] BohnerGéza, 2010-01-10 15:27:53
[1358] BohnerGéza2010-01-10 15:27:53

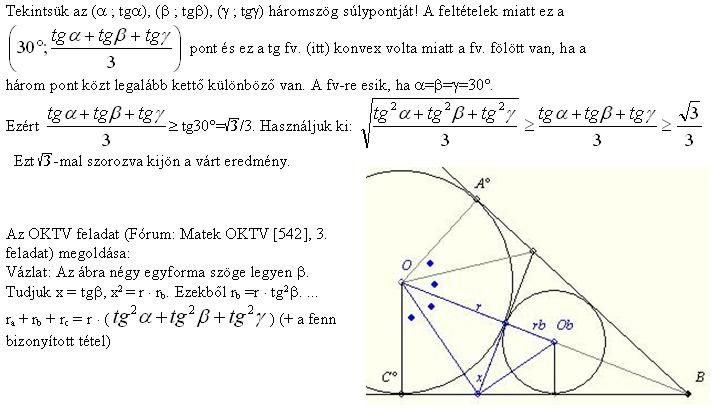
Az alábbi feladat felhasználható az OKTV - 2009-9010. II. kategória 3. feladatánál, de önmagában is jó feladat.

Használjuk ki a tg fv. tulajdonságait!

[1357] sakkmath2010-01-07 15:49:02

Igen, jól. A piros és a szaggatott vonalas háromszög a keresett két háromszög.

Előzmény: [1356] BohnerGéza, 2010-01-07 14:53:53
[1356] BohnerGéza2010-01-07 14:53:53

Jól értelmezem?

Előzmény: [1355] sakkmath, 2010-01-06 16:51:48
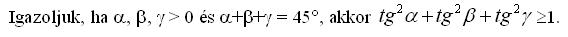[1355] sakkmath2010-01-06 16:51:48

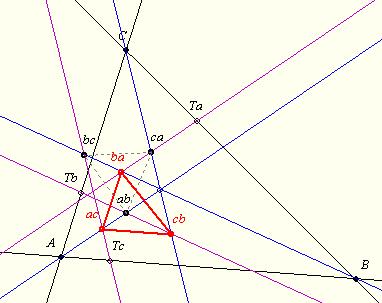
A következő feladatomat ajánlom megoldásra. (A megoldás végén valószínűleg elkerülhetetlen lesz számítógépes program használata. Ha ezért kissé kilógna e topicból, elnézést ... .)

(Kb.) 162. feladat: Egy hegyesszögű, nem egyenlő szárú háromszög területe T, oldalainak hossza a, b és c. A háromszög valamennyi magassági talppontján át húzzunk párhuzamost a talpponti oldallal szemközti csúcs szögfelezőjével. Tekintsük az így kapott egyeneseknek a szögfelező egyenesekkel alkotott metszéspontjait. Bizonyítsuk be, hogy e pontok két egyenlő területű háromszöget határoznak meg, melyek t1, illetve t2 nagyságú területére:

[1354] HoA2010-01-06 11:16:29

Egyetértek. De ha már előjött a kérdés, járjunk a végére. sin 2\alpha = 2 sin \alpha cos \alpha = 2 \cdot \frac {a}{2 R } \cdot \frac {b^2 + c^2 - a^2}{2 b c} Hasonlóan sin 2 \beta = 2 \cdot \frac {b}{2 R } \cdot \frac {c^2 + a^2 - b^2}{2 c a} A kettő hányadosa

\frac {sin 2\alpha }{ sin 2 \beta } = \frac {a}{b} \frac {a (b^2 + c^2 - a^2) }{b(c^2 + a^2 - b^2)} = \frac {a^2 (b^2 + c^2 - a^2) }{b^2 (c^2 + a^2 - b^2)}

, a módszer helyes.

Előzmény: [1351] SmallPotato, 2010-01-05 22:44:52
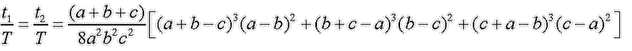[1353] laci7772010-01-05 22:59:40

Hát igen... Nekem meg épp ez a feladat volt elsőre (meg másodikra is...:P) megoldhatatlan.

Azért szerintem a túlzott szerénységre nincs okod:)

Köszönöm és további szép estét: Laci

Előzmény: [1352] SmallPotato, 2010-01-05 22:47:32
[1352] SmallPotato2010-01-05 22:47:32

Nagyon szívesen - én köszönöm a dícséretet. :-)

Itt az a jó, hogy mindenki talál a maga szintjéhaz illő "kihívást". Nekem épp ez a feladat jött be.

Előzmény: [1350] laci777, 2010-01-05 22:43:06
[1351] SmallPotato2010-01-05 22:44:52

[1341] és eredete

Fiatal barátunk kissé türelmetlen, egyszersmind bizalmatlan is, már bocsánat.

Ha levezetni nem akarja, legalább bízna a tudásban és a jóakaratban ... (amúgy az indexen is két helyen is közzétette a problémáját.)

Előzmény: [1349] HoA, 2010-01-05 22:31:51
[1350] laci7772010-01-05 22:43:06

Kedves SmallPotato!

Nagyon szépen köszönöm az elegáns megoldást - bár lehet, itt ez a példa nem lehetett komolyabb kihívás.

Nem vettem észre a hasonló háromszögeket (sem)...

Még egyszer köszönöm!

További szép estét, szia: Laci

Előzmény: [1348] SmallPotato, 2010-01-05 22:15:41
[1349] HoA2010-01-05 22:31:51

Ja, az más. Ha biztosra akarsz menni, használd [1343] lépéseit. Vagy kérdezd meg [1341] szerzőjét, ő hogy jutott erre az eredményre.

Előzmény: [1346] Tym0, 2010-01-05 21:17:10
[1348] SmallPotato2010-01-05 22:15:41

A hasonló háromszögekből, jelöléseiddel:

\frac r m = \frac {R} {\sqrt{r^2+m^2}-r}

Ebbe helyettesítsd be m-et az általad felírt képletből kifejezve, és oldd meg a kapott egyenletet r-re.

Előzmény: [1347] SmallPotato, 2010-01-05 22:09:51
[1347] SmallPotato2010-01-05 22:09:51

Rajzold fel az elrendezésnek a kúp tengelyén átmenő síkmetszetét. Rajzold be a gömb két sugarát: a kúp alapkörének középpontjába irányulót és az alkotóra merőlegest. Az ábrádon két hasonló derékszögű háromszög lesz: az egyiknek a befogói a kúp alapkörének sugara és a kúp magassága, a másiknak a befogói az alkotóra merőlegesen berajzolt gömbsugár és az alkotónak a kúp csúcsa felé eső szelete. Írd fel a befogók arányát mindkét háromszögben.

Előzmény: [1342] laci777, 2010-01-05 19:41:20

  [1]    [2]    [3]    [4]    [5]    [6]    [7]    [8]    [9]    [10]    [11]    [12]    [13]    [14]    [15]    [16]    [17]    [18]    [19]    [20]    [21]    [22]    [23]    [24]    [25]    [26]    [27]    [28]    [29]    [30]    [31]    [32]    [33]    [34]    [35]    [36]    [37]    [38]    [39]    [40]    [41]    [42]    [43]    [44]    [45]    [46]    [47]    [48]    [49]    [50]    [51]    [52]    [53]    [54]    [55]    [56]    [57]    [58]    [59]    [60]    [61]    [62]    [63]    [64]    [65]    [66]    [67]    [68]    [69]    [70]    [71]    [72]    [73]    [74]    [75]    [76]    [77]    [78]