Fórum: GEOMETRIA

Ezt a feladatot talán ismeritek.

Igaz-e, hogy minden tetraédernek legalább két oldala van, amin megáll (ha lerakjuk vízszintes terepre)?

Ja...........! Úgy már minden más.

Azt hiszem rájöttem, mi a félreértés oka. Az 1) feltétel azt jelenti, hogy az ÖSSZES pont nem lehet egy síkban.

Valamit félreérthetsz. A feladat szerint az 1), 2) és és 3) feltételnek teljesülnie kell. Akkor miért teszed fel, hogy ezek közül kettő nem teljesül ?

De ha az 1) és a 3) feltétel egyszerre nem teljesül, akkor a feladatra mindenképp nemleges a válasz...

...szerintem...

Tény, hogy a párhuzamos egyeneseket meghatározó pontok egy síkban vannak, de ebből én nem látom az ellentmondást... Szerintem te az első feltételt akartad megdönteni, de hát attól még, hogy bizonyos pontnégyesek egy síkban vannak, nem feltétlenül van minden pont egy síkban.

(érvelésedre egyébként lejjebb találsz ellenpéldát...)

Ha AB és CD szakasz (s így azegyenes) párhuzamos, akkor nem kitérőek, és nem metszik egymást, ezért az ABCD négyszög egy síkidom, sőt egy trapéz, tehát ilyen "pontrendszer" nem létezik.

Talán a legegyszerűbb/legelegánsabb megoldás az, ha veszel egy szabályos 1004-szöget, majd két szemközti csúcsánál fogva 90 fokkal kiforgatod a térbe, s ehhez hozzáveszed az eredetit.

Köszi. Hiába kerestem a neten, nem találtam.

Ez idei Kürschák-példa volt:) azt hiszem, ilyesmi jó: egy gömb egy főkörén egy szabályos 2002-szög, valamint ezen 2002-szög két szemközti csúcsára illeszkedő, a korábbi főkörre merőleges főkörön egy szabályos hatszög (mármint, hogy 2 szemközti csúcsa egybeessen a 2002-szög szemközti csúcsaival).

Sziasztok !

Van egy példám, amivel nem boldogulok. Állítólag versenypélda, de sehol sem találom.

Megadható-e a 3-dimenziós térben 2006 pont a következő tulajdonságokkal:

1) a pontok nincsenek egy síkban

2) semelyik 3 nincs egy egyenesen

3) bármely A,B ponthoz létezik olyan C,D pont, hogy az AB szakasz párhuzamos a CD szakasszal

huuuuuuu Nagyon tuti kis progi lett. Le a kalappal. Köszönöm szépen :D

El.

Sirpi. Elkészült az a kis feet a progidhoz, ami megmondja, h milyen tipusú négyzetből mennyit használ fel?

Kicsit visszatérnék a négyzetredarabolás problémájához, pontosabban ehhez kapcsolódóan egy hasonló problémához. Régebb óta foglalkoztat egy hasonló probléma. Adott (itt most) egy négyzet és ezt kell valahány kisebb négyzetre felosztani. Én a 11 részre osztás változatba merültem el, többszöri nekifutással.

Mit gondoltok, hányféle különböző (egymásba nem forgatható vagy tükrözhető) módon lehet egy négyzetet 11 kisebb négyzetre osztani? Először kiváncsi vagyok a megérzésetekre. Utána, ha nem bonyolult, valaki írhatna rá egy rutint, mert kiváncsi lennék a pontos eredményre is.

Ez egy maximális összsúlyú út keresése egy irányított körmentes gráfban. Ugyanis feleltessünk meg minden kockát egy-egy csúcsnak. Tekintsük ezt az n csúcsot abban a sorrendben ahogy a nekik megfelelő kockák az asztalon vannak (a₁,a₂,...,a_n). Ha i<j és a_j kocka könnyebb, valamint keskenyebb mint a_i kocka, akkor mutasson él a_i-ből a_j-be. Súlyozzunk minden a_ia_j élet -vel, ahol |a_i| = a_i szélessége (ami megegyezik a magasságával). Vegyünk fel továbbá egy s ill. t csúcsot, s-et első, t-t utolsó csúcsnak. És mutasson él s-ből minden a_i-be, ezek legyenek súlyozva -vel. Illetve minden a_i-ből mutasson él t-be szintén súlyozással. A csúcsok jelenlegi helyzete egy topológikus sorrend (csak előre megy él), ebben a következőképpen kereshetjük meg a leghosszabb utat (s:=a₀, t:=a_n+1): Az a_i pontra ha nincs a_i-be futó él, akkor címkéje legyen 0, egyébként P_i azon pontok halmaza ahonnan van él a_i-be. Az a_i pont címkéje = címkéje +c_ji}, ahol c_ji az a_ia_j él súlya.

Vagy épp jóval nehezebb. Nem tudom.

Most esett le, hogy mit mond ez a feladat. Figyelmesebben kéne olvasnom. Tehát a kockákat csak sorban lehet felhasználni. Így, azt hiszem, jóval könnyebb.

Viszont az átlatános táblázat benne van: A113881.

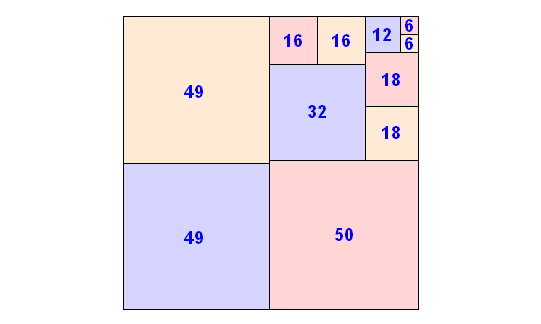
Ha megnézzük, hogy egy n+1 x n méretű téglalapot hány részre kell a szabályok szerint szétvágni, akkor egy ilyen sorozat jön ki.

2, 3, 4, 5, 5, 5, 7, 7, 6, 6, 7, 7, 7, 7, 7, 9, 8, 8, 9, 8, 8, 8, 8, 8, 8, 8, 9, 9, 9, 9, 11, 9, 9, 9, 9, 10, 9, 9, 9, 9, 9, 9, 10, 10, 10, 10, 10, 10, 10, 10, 10, 11, 10, 10, 12, 10, 10, 10, 10, 10, 10, 10, 11, 10, 10, 11, 12, 11, 11, 11, 12, 12, 11, 11, 11, 11, 11, 11, 12, 12, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 12, 11, 11, 11, 11, 11, 11, 11, 12, 12, 11, 11, 11, 11, 11, 11, 12, 12, 12, 12, 12, 12, 12, 12, 12, 13, 12, 12, 12, 12, 12, 12, 12, 13, 12, 12, 15, 12, 12, 12, 12, 12, 12, 12, 12, 13, 12, 12, 12, 12, 12, 12, 12, 13, 13, 13, 13, 13, 12, 12, 12, 12, 12, 12, 13, 13, 12, 12, 12, 12, 12, 12, 13, 12, 12, 12, 12, 12, 12, 12, 13, 13, 13, 13, 13, 13, 13, 13, 14, 13, 13, 13, 13, 13, 13, 13, 14, 14, 13, 13, 13, 13, 13, 13, 13, 14, 13, 13, 14, 13, 13, 13, 13, 13, 13, 13, 14, 13, 13, 13, 14, 13, 13, 13, 13, 13, 13, ...

Ez a sorozat (még) nincs benne az OEIS-ben.

Akkor itt van: vag.bmp.

Jaj. Így sem lehet, mert a fórum átalakítja jpeg-gé.

Akkor feltöltöm valahova.

Feltöltöm a programot is, ha valakit érdekel. Ez már egy módosított változat, 2501 [484] hozzászólásából elloptam az ötletet, valamint képbe ágyaztam.

Ez egy ruby program. Ha ki akarod próbálni, mentsd le vag.bmp néven, majd indítsd el a ruby vag.bmp paranccsal. (Bocs, de másképpen nem lehet ide programkódot feltölteni.)

Mivel nem tudok programot írni, felszerkesztettem:

Bele :-) Asszem tényleg átírom nemrekurzívra, ahogy 2501 mondta, és akkor ilyen finomságokat is bele lehet tenni. Nemsoká jelentkezem. Bár ugye a felbontás nem mindig egyértelmű, a progam max egy megoldást fog kiadni a sok közül.